主成分分析
基本的な考え方
(Press ? for help, n and p for next and previous slide)
村田 昇
講義概要
- 第1日 : 主成分分析の考え方
- 第2日 : 分析の評価と視覚化
主成分分析の考え方
主成分分析
- 多数の変量のもつ情報の分析・視覚化
- 変量を効率的に縮約して少数の特徴量を構成する
- 特徴量に関与する変量間の関係を明らかにする
- PCA (Principal Component Analysis)
- 構成する特徴量 : 主成分 (princial component)
主成分分析の例
| 都道府県名 | 地方区分 | 昼夜人口比 | 年少人口比 | 老年人口比 | 人口増減率 | 粗出生率 | 粗死亡率 | 婚姻率 | 離婚率 |
|---|---|---|---|---|---|---|---|---|---|
| 北海道 | 北海道 | 100.0 | 11.7 | 26.0 | -0.47 | 7.09 | 10.63 | 4.86 | 2.12 |
| 青森県 | 東北 | 100.0 | 12.1 | 27.0 | -0.95 | 6.79 | 12.81 | 4.33 | 1.78 |
| 岩手県 | 東北 | 99.7 | 12.4 | 27.9 | -0.84 | 7.12 | 12.33 | 4.32 | 1.52 |
| 宮城県 | 東北 | 100.2 | 13.0 | 22.9 | -0.09 | 8.05 | 9.51 | 5.30 | 1.70 |
| 秋田県 | 東北 | 99.9 | 11.1 | 30.7 | -1.12 | 6.16 | 13.98 | 3.78 | 1.41 |
| 山形県 | 東北 | 99.8 | 12.6 | 28.3 | -0.78 | 7.13 | 12.81 | 4.24 | 1.46 |
| 福島県 | 東北 | 99.6 | 12.9 | 26.1 | -1.41 | 7.02 | 11.94 | 4.73 | 1.64 |
| 茨城県 | 関東 | 97.2 | 13.2 | 23.8 | -0.51 | 7.78 | 10.20 | 4.92 | 1.79 |
| 栃木県 | 関東 | 99.1 | 13.2 | 23.2 | -0.40 | 8.02 | 10.43 | 5.13 | 1.85 |
| 群馬県 | 関東 | 99.9 | 13.4 | 24.9 | -0.45 | 7.49 | 10.63 | 4.64 | 1.77 |
| 埼玉県 | 関東 | 88.6 | 13.0 | 22.0 | 0.07 | 7.90 | 8.20 | 5.10 | 1.86 |
| 千葉県 | 関東 | 89.5 | 12.8 | 23.2 | -0.31 | 7.89 | 8.59 | 5.19 | 1.86 |
| 東京都 | 関東 | 118.4 | 11.3 | 21.3 | 0.26 | 8.12 | 8.25 | 6.75 | 1.91 |
| 神奈川県 | 関東 | 91.2 | 13.0 | 21.5 | 0.10 | 8.32 | 7.94 | 5.68 | 1.85 |
| 新潟県 | 中部 | 100.0 | 12.5 | 27.2 | -0.64 | 7.45 | 11.97 | 4.35 | 1.37 |
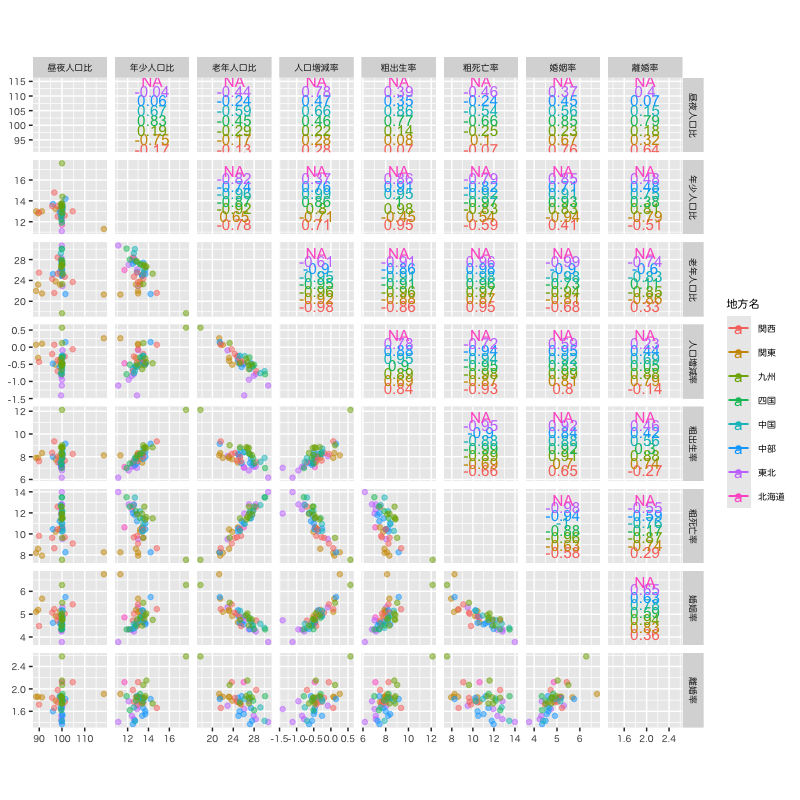
Figure 1: 人口関連データの散布図
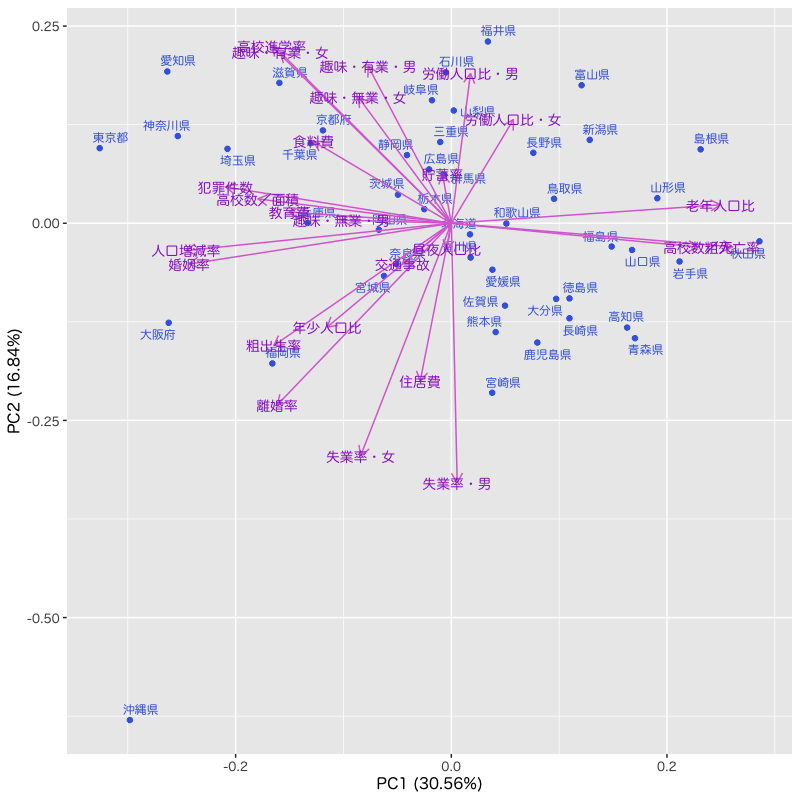
Figure 2: 主成分得点のバイプロット
分析の枠組み
- \(x_{1},\dotsc,x_{p}\) : 変数
- \(z_{1},\dotsc,z_{d}\) : 特徴量 ( \(d\leq p\) )
変数と特徴量の関係 (線形結合)
\begin{equation} z_k=a_{1k}x_{1}+\cdots+a_{pk}x_{p}\quad(k=1,\dotsc,d) \end{equation}特徴量は定数倍の任意性があるので以下を仮定
\begin{equation} \|\boldsymbol{a}_k\|^2=\sum_{j=1}^pa_{jk}^2=1 \end{equation}
主成分分析の用語
- 特徴量 \(z_k\)
- 第 \(k\) 主成分得点 (principal component score)
- 第 \(k\) 主成分
- 係数ベクトル \(\boldsymbol{a}_k\)
- 第 \(k\) 主成分負荷量 (principal component loading)
- 第 \(k\) 主成分方向 (principal component direction)
分析の目的
目的
主成分得点 \(z_{1},\dots,z_{d}\) が変数 \(x_{1},\dotsc,x_{p}\) の情報を効率よく反映するように主成分負荷量 \(\boldsymbol{a}_{1},\dotsc,\boldsymbol{a}_{d}\) を観測データから決定する
- 分析の方針 (以下は同値)
- データの情報を最も保持する変量の 線形結合を構成
- データの情報を最も反映する 座標軸を探索
- 教師なし学習 の代表的手法の1つ
- 特徴抽出 : 情報処理に重要な特性を変数に凝集
- 次元縮約 : 入力をできるだけ少ない変数で表現
実習
第1主成分の計算
記号の準備
- 変数 : \(x_{1},\dotsc,x_{p}\) (\(p\)次元)
観測データ : \(n\) 個の \((x_{1},\dotsc,x_{p})\) の組
\begin{equation} \{(x_{i1},\dots,x_{ip})\}_{i=1}^n \end{equation}- ベクトル表現
- \(\boldsymbol{x}_{i}=(x_{i1},\dots,x_{ip})^{\mathsf{T}}\) : \(i\) 番目の観測データ (\(p\) 次元空間内の1点)
- \(\boldsymbol{a}=(a_{1},\dots,a_{p})^{\mathsf{T}}\) : 長さ1の \(p\) 次元ベクトル
係数ベクトルによる射影
データ \(\boldsymbol{x}_{i}\) の \(\boldsymbol{a}\) 方向成分の長さ
\begin{equation} \boldsymbol{a}^{\mathsf{T}}\boldsymbol{x}_{i} \quad\text{(スカラー)} \end{equation}方向ベクトル \(\boldsymbol{a}\) をもつ直線上への点 \(\boldsymbol{x}_{i}\) の直交射影
\begin{equation} (\boldsymbol{a}^{\mathsf{T}}\boldsymbol{x}_{i})\,\boldsymbol{a} \quad\text{(スカラー \(\times\) ベクトル)} \end{equation}
幾何学的描像
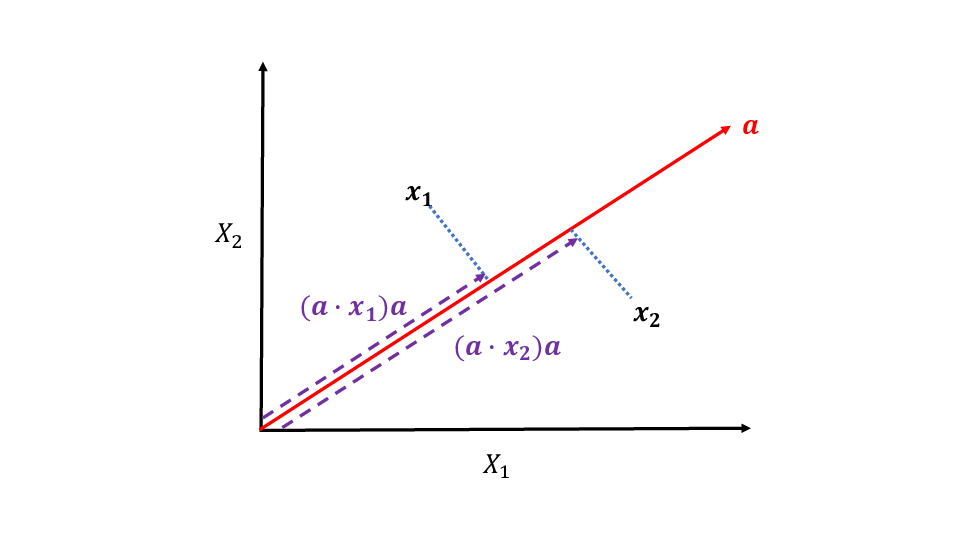
Figure 3: 観測データの直交射影 (\(p=2,n=2\) の場合)
ベクトル \(\boldsymbol{a}\) の選択の指針
射影による特徴量の構成
ベクトル \(\boldsymbol{a}\) を うまく 選んで 観測データ \(\boldsymbol{x}_{1},\cdots,\boldsymbol{x}_{n}\) の情報を最も保持する1変量データ \(z_{1},\cdots,z_{n}\)を構成
\begin{equation} z_{1}=\boldsymbol{a}^{\mathsf{T}}\boldsymbol{x}_{1}, z_{2}=\boldsymbol{a}^{\mathsf{T}}\boldsymbol{x}_2, \dotsc, z_{n}=\boldsymbol{a}^{\mathsf{T}}\boldsymbol{x}_n \end{equation}特徴量のばらつきの最大化
観測データの ばらつき を最も反映するベクトル \(\boldsymbol{a}\) を選択
\begin{equation} \arg\max_{\boldsymbol{a}} \sum_{i=1}^n(\boldsymbol{a}^{\mathsf{T}}\boldsymbol{x}_{i} -\boldsymbol{a}^{\mathsf{T}}\bar{\boldsymbol{x}})^2, \quad \bar{\boldsymbol{x}} = \frac{1}{n}\sum_{i=1}^n\boldsymbol{x}_{i}, \end{equation}
ベクトル \(\boldsymbol{a}\) の最適化
最適化問題
制約条件 \(\|\boldsymbol{a}\|=1\) の下で 以下の関数を最大化せよ
\begin{equation} f(\boldsymbol{a}) = \sum_{i=1}^n(\boldsymbol{a}^{\mathsf{T}}\boldsymbol{x}_{i} -\boldsymbol{a}^{\mathsf{T}}\bar{\boldsymbol{x}})^2 \end{equation}- この最大化問題は必ず解をもつ
- \(f(\boldsymbol{a})\) は連続関数
- 集合 \(\{\boldsymbol{a}\in\mathbb{R}^p:\|\boldsymbol{a}\|=1\}\) はコンパクト(有界閉集合)
第1主成分の解
行列による表現
中心化したデータ行列
\begin{equation} X = \begin{pmatrix} \boldsymbol{x}_{1}^{\mathsf{T}}-\bar{\boldsymbol{x}}^{\mathsf{T}} \\ \vdots \\ \boldsymbol{x}_{n}^{\mathsf{T}}-\bar{\boldsymbol{x}}^{\mathsf{T}} \end{pmatrix} = \begin{pmatrix} x_{11}-\bar{x}_{1} & \cdots & x_{1p}-\bar{x}_{p}\\ \vdots & & \vdots \\ x_{n1}-\bar{x}_{1} & \cdots & x_{np}-\bar{x}_{p} \end{pmatrix} \end{equation}評価関数 \(f(\boldsymbol{a})\) は行列 \(X^{\mathsf{T}}X\) の二次形式
\begin{equation} f(\boldsymbol{a}) = \boldsymbol{a}^{\mathsf{T}}X^{\mathsf{T}}X\boldsymbol{a} \end{equation}
ベクトル \(\boldsymbol{a}\) の解
最適化問題
\begin{equation} \text{maximize}\quad f(\boldsymbol{a}) = \boldsymbol{a}^{\mathsf{T}}X^{\mathsf{T}}X\boldsymbol{a} \quad\text{s.t.}\quad \boldsymbol{a}^{\mathsf{T}}\boldsymbol{a}=1 \end{equation}
制約付き最適化なので未定係数法を用いればよい
\begin{equation} L(\boldsymbol{a},\lambda) =f(\boldsymbol{a})+\lambda(1-\boldsymbol{a}^{\mathsf{T}}\boldsymbol{a}) \end{equation}の鞍点
\begin{equation} \frac{\partial}{\partial\boldsymbol{a}}L(\boldsymbol{a},\lambda) =0 \end{equation}を求めればよいので
\begin{align} 2X^{\mathsf{T}}X\boldsymbol{a}-2\lambda\boldsymbol{a} &=0\\ X^{\mathsf{T}}X\boldsymbol{a} &=\lambda\boldsymbol{a} \quad\text{(固有値問題)} \end{align}
解の条件
\(f(\boldsymbol{a})\) の極大値を与える \(\boldsymbol{a}\) は \(X^{\mathsf{T}}X\) の固有ベクトルとなる
\begin{equation} X^{\mathsf{T}}X\boldsymbol{a} = \lambda\boldsymbol{a} \end{equation}
第1主成分
固有ベクトル\(\boldsymbol{a}\)に対する\(f(\boldsymbol{a})\) は行列 \(X^{\mathsf{T}}X\) の固有値
\begin{equation} f(\boldsymbol{a}) =\boldsymbol{a}^{\mathsf{T}}X^{\mathsf{T}}X\boldsymbol{a} =\boldsymbol{a}^{\mathsf{T}}\lambda\boldsymbol{a} =\lambda \end{equation}- 求める \(\boldsymbol{a}\) は行列 \(X^{\mathsf{T}}X\) の最大固有ベクトル (長さ1)
- 第1主成分負荷量 : 最大(第一)固有ベクトル \(\boldsymbol{a}\)
第1主成分得点
\begin{equation} z_{i1} =a_{1}x_{i1}+\cdots+a_{p}x_{ip} =\boldsymbol{a}^{\mathsf{T}}\boldsymbol{x}_{i}, \quad(i=1,\dots,n) \end{equation}
実習
Gram 行列の性質
Gram 行列の固有値
- \(X^{\mathsf{T}}X\) は半正定値行列
- \(X^{\mathsf{T}}X\) の固有値は0以上の実数
固有値を重複を許して降順に並べる
\begin{equation} \lambda_{1}\geq\dotsb\geq\lambda_{p}\quad(\geq0) \end{equation}固有値 \(\lambda_{k}\) に対する固有ベクトルを \(\boldsymbol{a}_{k}\)(長さ1)とする
\begin{equation} \|\boldsymbol{a}_{k}\|=1, \quad (k=1,\dotsc,p) \end{equation}
Gram 行列のスペクトル分解
\(\boldsymbol{a}_{1},\dotsc,\boldsymbol{a}_{p}\) は 互いに直交 するようとることができる
\begin{equation} j\neq k \quad\Rightarrow\quad \boldsymbol{a}_{j}^{\mathsf{T}}\boldsymbol{a}_k=0 \end{equation}行列 \(X^{\mathsf{T}}X\) (半正定値行列) のスペクトル分解
\begin{align} X^{\mathsf{T}}X &=\lambda_{1}\boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}}+ \lambda_{2}\boldsymbol{a}_{2}\boldsymbol{a}_{2}^{\mathsf{T}}+ \dotsb+\lambda_{p}\boldsymbol{a}_{p}\boldsymbol{a}_{p}^{\mathsf{T}}\\ &=\sum_{k=1}^{p}\lambda_{k}\boldsymbol{a}_{k}\boldsymbol{a}_{k}^{\mathsf{T}} \end{align}- 固有値と固有ベクトルによる行列の表現
第2主成分以降の計算
第2主成分の考え方
- 第1主成分
- 主成分負荷量 : ベクトル \(\boldsymbol{a}_{1}\)
- 主成分得点 : \(\boldsymbol{a}_{1}^{\mathsf{T}}\boldsymbol{x}_{i}\) (\(i=1,\dotsc,n\))
第1主成分負荷量に関してデータが有する情報
\begin{equation} (\boldsymbol{a}_{1}^{\mathsf{T}}\boldsymbol{x}_{i})\,\boldsymbol{a}_{1} \quad(i=1,\dotsc,n) \end{equation}第1主成分を取り除いた観測データ (分析対象)
\begin{equation} \tilde{\boldsymbol{x}}_{i} = \boldsymbol{x}_{i} -(\boldsymbol{a}_{1}^{\mathsf{T}}\boldsymbol{x}_{i})\,\boldsymbol{a}_{1} \quad(i=1,\dotsc,n) \end{equation}
第2主成分の最適化
最適化問題
制約条件 \(\|\boldsymbol{a}\|=1\) の下で 以下の関数を最大化せよ
\begin{equation} \tilde{f}(\boldsymbol{a}) = \sum_{i=1}^n(\boldsymbol{a}^{\mathsf{T}}\tilde{\boldsymbol{x}}_{i} -\boldsymbol{a}^{\mathsf{T}}\bar{\tilde{\boldsymbol{x}}})^2 \quad\text{ただし}\quad \bar{\tilde{\boldsymbol{x}}} = \frac{1}{n}\sum_{i=1}^n\tilde{\boldsymbol{x}}_{i} \end{equation}
第2主成分以降の解
行列による表現
中心化したデータ行列
\begin{equation} \tilde{X} = \begin{pmatrix} \tilde{\boldsymbol{x}}_{1}^{\mathsf{T}}-\bar{\tilde{\boldsymbol{x}}}^{\mathsf{T}} \\ \vdots \\ \tilde{\boldsymbol{x}}_{n}^{\mathsf{T}}-\bar{\tilde{\boldsymbol{x}}}^{\mathsf{T}} \end{pmatrix} = X-X\boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}} \end{equation}
Gram 行列
\begin{align} \tilde{X}^{\mathsf{T}}\tilde{X} &= (X-X\boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}})^{\mathsf{T}} (X-X\boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}})\\ &= X^{\mathsf{T}}X - X^{\mathsf{T}}X\boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}} - \boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}}X^{\mathsf{T}}X + \boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}}X^{\mathsf{T}}X \boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}}\\ &= X^{\mathsf{T}}X - \lambda_{1}\boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}} - \lambda_{1}\boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}} + \lambda_{1}\boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}} \boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}}\\ &= X^{\mathsf{T}}X - \lambda_{1}\boldsymbol{a}_{1}\boldsymbol{a}_{1}^{\mathsf{T}}\\ &= \sum_{k=2}^{p}\lambda_{k}\boldsymbol{a}_{k}\boldsymbol{a}_{k}^{\mathsf{T}} \end{align}
第2主成分
Gram 行列 \(\tilde{X}^{\mathsf{T}}\tilde{X}\) の固有ベクトル \(\boldsymbol{a}_{1}\) の固有値は 0
\begin{equation} \tilde{X}^{\mathsf{T}}\tilde{X}\boldsymbol{a}_{1} = 0 \end{equation}- Gram 行列 \(\tilde{X}^{\mathsf{T}}\tilde{X}\) の最大固有値は \(\lambda_2\)
- 解は第2固有値 \(\lambda_2\) に対応する固有ベクトル \(\boldsymbol{a}_2\)
- 以下同様に 第 \(k\) 主成分負荷量は \(X^{\mathsf{T}}X\) の第 \(k\) 固有値 \(\lambda_k\) に対応する固有ベクトル \(\boldsymbol{a}_k\)
実習
次回の予定
- 第1日 : 主成分分析の考え方
- 第2日 : 分析の評価と視覚化