回帰分析

回帰モデルの考え方と推定

(Press ? for help, n and p for next and previous slide)

村田昇

講義概要

第1回 : 回帰モデルの考え方と推定
第2回 : モデルの評価
第3回 : モデルによる予測と発展的なモデル

回帰分析の考え方

回帰分析

ある変量を別の変量で説明する関係式を構成する
関係式 : 回帰式 (regression equation)
- 説明される側 : 目的変数, 被説明変数, 従属変数, 応答変数
- 説明する側 : 説明変数, 独立変数, 共変量
説明変数の数による分類
- 一つの場合 : 単回帰 (simple regression)
- 複数の場合 : 重回帰 (multiple regression)

一般の回帰の枠組

説明変数 : \(x_1,\dotsc,x_p\) (p次元)
目的変数 : \(y\) (1次元)
回帰式 : \(y\) を \(x_1,\dotsc,x_p\) で説明するための関係式

\begin{equation} y=f(x_1,\dotsc,x_p) \end{equation}
観測データ : n個の \((y,x_1,\dotsc,x_p)\) の組

\begin{equation} \{(y_i,x_{i1},\dotsc,x_{ip})\}_{i=1}^n \end{equation}

線形回帰

任意の \(f\) では一般的すぎて分析に不向き
\(f\) として 1次関数 を考える

ある定数 \(\beta_0,\beta_1,\dots,\beta_p\) を用いた式 :

\begin{equation} f(x_1,\dots,x_p)=\beta_0+\beta_1x_1+\cdots+\beta_px_p \end{equation}
- 1次関数の場合 : 線形回帰 (linear regression)
- 一般の場合 : 非線形回帰 (nonlinear regression)
非線形関係は新たな説明変数の導入で対応可能
- 適切な多項式 : \(x_j^2, x_jx_k, x_jx_kx_l,\dotsc\)
- その他の非線形変換 : \(\log x_j, x_j^\alpha,\dotsc\)
- 全ての非線形関係ではないことに注意

回帰係数

線形回帰式

\begin{equation} y=\beta_0+\beta_1x_1+\cdots+\beta_px_p \end{equation}
- \(\beta_0,\beta_1,\dots,\beta_p\) : 回帰係数 (regression coefficients)
- \(\beta_0\) : 定数項 / 切片 (constant term / intersection)
線形回帰分析 (linear regression analysis)
- 未知の回帰係数をデータから決定する分析方法
- 決定された回帰係数の統計的な性質を診断

回帰の確率モデル

回帰式の不確定性
- データは一般に観測誤差などランダムな変動を含む
- 回帰式がそのまま成立することは期待できない
確率モデル : データのばらつきを表す項 \(\epsilon_i\) を追加

\begin{equation} y_i=\beta_0+\beta_1 x_{i1}+\cdots+\beta_px_{ip}+\epsilon_i\quad (i=1,\dots,n) \end{equation}
- \(\epsilon_1,\dots,\epsilon_n\) : 誤差項 / 撹乱項 (error / disturbance term)
  - 誤差項は独立な確率変数と仮定
  - 多くの場合，平均0，分散 \(\sigma^2\) の正規分布を仮定
推定 (estimation) : 観測データから回帰係数を決定

回帰係数の推定

残差

残差 (residual) : 回帰式で説明できない変動
回帰係数 \(\boldsymbol{\beta}=(\beta_0,\beta_1,\dotsc,\beta_p)^{\mathsf{T}}\) を持つ回帰式の残差

\begin{equation} e_i(\boldsymbol{\beta})= y_i-(\beta_0+\beta_1 x_{i1}+\dotsb+\beta_px_{ip}) \quad (i=1,\dotsc,n) \end{equation}
残差 \(e_i(\boldsymbol{\beta})\) の絶対値が小さいほど当てはまりがよい

最小二乗法

残差平方和 (residual sum of squares)

\begin{equation} S(\boldsymbol{\beta}) = \sum_{i=1}^ne_i(\boldsymbol{\beta})^2 \end{equation}
最小二乗推定量 (least squares estimator)

残差平方和 \(S(\boldsymbol{\beta})\) を最小にする \(\boldsymbol{\beta}\)

\begin{equation} \boldsymbol{\hat{\beta}} = (\hat{\beta}_0,\hat{\beta}_1,\dotsc,\hat{\beta}_p)^{\mathsf{T}} = \arg\min_{\boldsymbol{\beta}}S(\boldsymbol{\beta}) \end{equation}

行列の定義

デザイン行列 (design matrix)

\begin{equation} X= \begin{pmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1p} \\ 1 & x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \vdots & & \vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{np} \end{pmatrix} \end{equation}
- \(n\times(p{+}1)\)行列

ベクトルの定義

目的変数，誤差，回帰係数のベクトル

\begin{equation} \boldsymbol{y}= \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix},\quad \boldsymbol{\epsilon}= \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \end{pmatrix},\quad \boldsymbol{\beta}= \begin{pmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_p \end{pmatrix} \end{equation}
- \(\boldsymbol{y},\boldsymbol{\epsilon}\) は\(n\)次元ベクトル
- \(\boldsymbol{\beta}\) は\(p{+}1\)次元ベクトル

行列・ベクトルによる表現

確率モデル

\begin{equation} \boldsymbol{y} =X\boldsymbol{\beta}+\boldsymbol{\epsilon} \end{equation}
残差平方和

\begin{equation} S(\boldsymbol{\beta}) =(\boldsymbol{y}-X\boldsymbol{\beta})^{\mathsf{T}} (\boldsymbol{y}-X\boldsymbol{\beta}) \end{equation}

解の条件

解 \(\boldsymbol{\beta}\) では残差平方和の勾配は零ベクトル

\begin{equation} \nabla S(\boldsymbol{\beta})= \Bigl( \frac{\partial S}{\partial\beta_0}(\boldsymbol{\beta}), \frac{\partial S}{\partial\beta_1}(\boldsymbol{\beta}),\dotsc, \frac{\partial S}{\partial\beta_p}(\boldsymbol{\beta}) \Bigr)^\mathsf{T}=\boldsymbol{0} \end{equation}
成分 (\(j=0,1,\dotsc,p\)) ごとの条件式

\begin{equation} \frac{\partial S}{\partial\beta_j}(\boldsymbol{\beta}) = -2\sum_{i=1}^n\Bigl(y_i-\sum_{k=0}^p\beta_kx_{ik}\Bigr)x_{ij} =0 \end{equation}

ただし \(x_{i0}=1\; (i=1,\dotsc,n)\)

正規方程式

正規方程式 (normal equation)

\begin{equation} X^{\mathsf{T}}X\boldsymbol{\beta} =X^{\mathsf{T}}\boldsymbol{y} \end{equation}
\(X^{\mathsf{T}}X\) : Gram行列 (Gram matrix)
- \((p{+}1)\times(p{+}1)\) 行列 (正方行列)
- 正定対称行列 (固有値が非負)

正規方程式の解

正規方程式の基本的な性質
- 正規方程式は必ず解をもつ (一意に決まらない場合もある)
- 正規方程式の解は最小二乗推定量であるための必要条件
解の一意性の条件
- Gram 行列 \(X^{\mathsf{T}}X\) が正則
- \(X\) の列ベクトルが独立 (後述)
正規方程式の解

\begin{equation} \boldsymbol{\hat{\beta}} = (X^{\mathsf{T}}X)^{-1}X^{\mathsf{T}}\boldsymbol{y} \end{equation}

実習

R : 線形モデルの推定

関数 stats::lm() による推定

lm(formula, data, subset, weights, na.action,
   method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,
   singular.ok = TRUE, contrasts = NULL, offset, ...)
#' formula: 目的変数名 ~ 説明変数名(複数ある場合は + で並べる)
#' data: 目的変数，説明変数を含むデータフレーム
#' subset: 推定に用いるデータフレームの部分集合を指定(指定しなければ全て)
#' na.action: 欠損の扱いを指定(既定値はoption("na.action")で設定された処理)
#' model,x,y,qr: 返値にmodel.frame,model.matrix,目的変数,QR分解を含むか指定

データセットの準備

回帰分析では以下のデータセットを使用する
- https://www.statlearning.com/s/Advertising.csv
  
  広告費(TV,radio,newspapers)と売上の関係を調べたもの
  - 参考 : https://www.statlearning.com
    
    “Datasets in this presentation are taken from ”An Introduction to Statistical Learning, with applications in R“ (Springer, 2013) with permission from the authors: G. James, D. Witten, T. Hastie and R. Tibshirani ”
- tokyo_weather.csv (配付)
  
  気象庁より取得した東京の気候データを回帰分析用に整理したもの
  - 参考 : https://www.data.jma.go.jp/gmd/risk/obsdl/index.php

練習問題

前掲のデータセットを用いて回帰式を構成しなさい
- 東京の8月の気候データ
```
formula = temp ~ solar + press
```
- 広告費と売上データ
```
formula = sales ~ TV 
formula = sales ~ radio
formula = sales ~ TV + radio
```

最小二乗推定量の性質

解析の上での良い条件

最小二乗推定量がただ一つだけ存在する条件
- \(X^{\mathsf{T}}X\) が正則
- \(X^{\mathsf{T}}X\) の階数が \(p{+}1\)
- \(X\) の階数が \(p{+}1\)
- \(X\) の列ベクトルが 1次独立
これらは同値条件

解析の上での良くない条件

説明変数が1次従属 : 多重共線性 (multicollinearity)
多重共線性が強くならないように説明変数を選択
- \(X\) の列(説明変数)の独立性を担保する
- 説明変数が互いに異なる情報をもつように選ぶ
- 似た性質をもつ説明変数の重複は避ける

推定の幾何学的解釈

あてはめ値 / 予測値 (fitted values / predicted values)

\begin{equation} \boldsymbol{\hat{y}} = X\boldsymbol{\hat{\beta}} = \hat{\beta}_{0} X_\text{第0列} + \dots + \hat{\beta}_{p} X_\text{第p列} \end{equation}

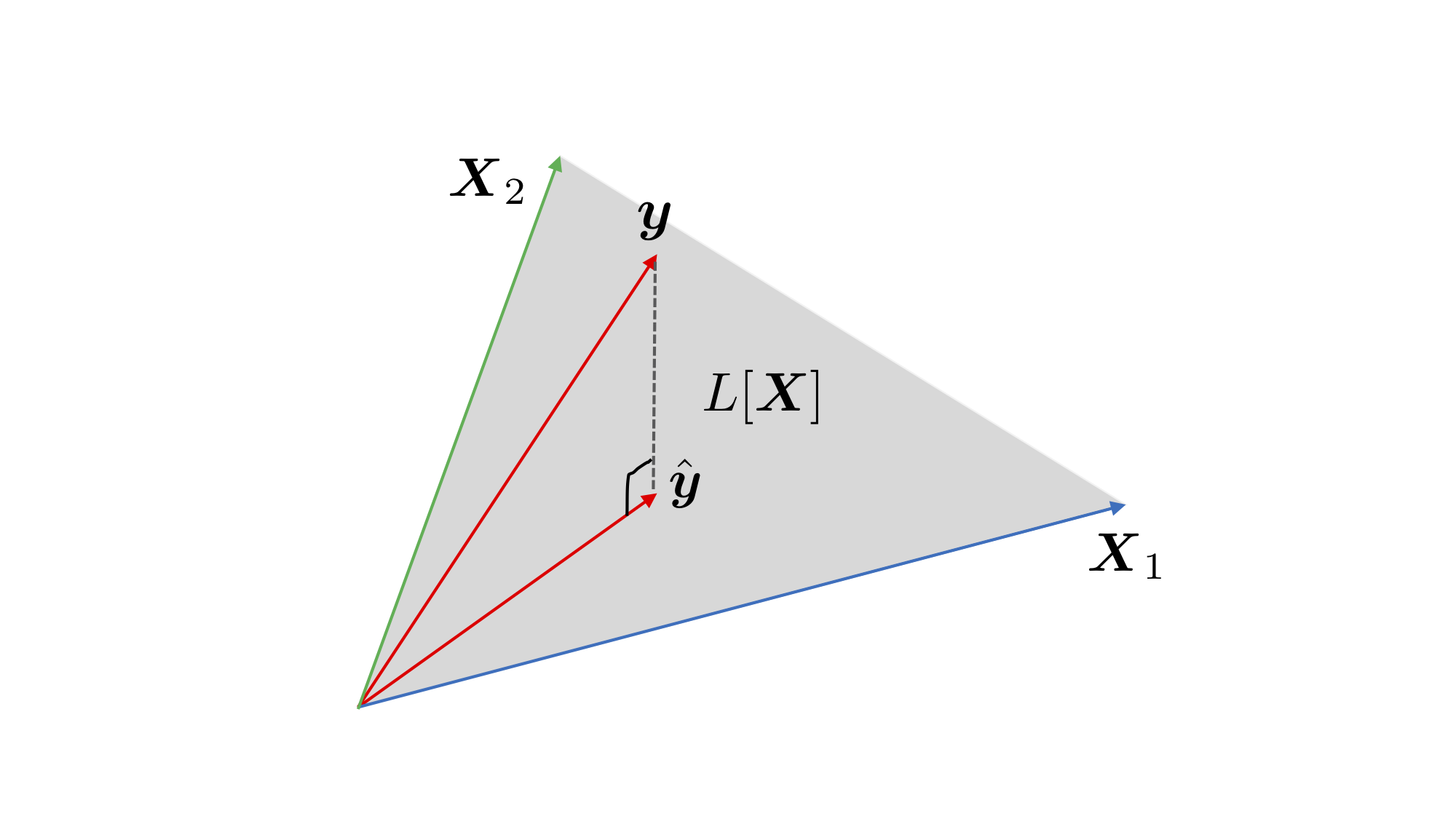
Figure 1: \(n=3\) , \(p+1=2\) の場合の最小二乗法による推定

最小二乗推定量 \(\boldsymbol{\hat{y}}\) の幾何学的性質
- \(L[X]\) : \(X\) の列ベクトルが張る \(\mathbb{R}^n\) の線形部分空間
- \(X\) の階数が \(p{+}1\) ならば \(L[X]\) の次元は \(p{+}1\) (解の一意性)
- \(\boldsymbol{\hat{y}}\) は \(\boldsymbol{y}\) の \(L[X]\) への直交射影
- 残差 (residuals) \(\boldsymbol{\hat{\epsilon}}=\boldsymbol{y}-\boldsymbol{\hat{y}}\) はあてはめ値 \(\boldsymbol{\hat{y}}\) に直交
  
  \begin{equation} \boldsymbol{\hat{\epsilon}}\cdot\boldsymbol{\hat{y}}=0 \end{equation}

線形回帰式と標本平均

\(\boldsymbol{x}_i=(x_{i1},\dotsc,x_{ip})^{\mathsf{T}}\): \(i\) 番目の観測データの説明変数
説明変数および目的変数の標本平均

\begin{align} \boldsymbol{\bar{x}} &=\frac{1}{n}\sum_{i=1}^n\boldsymbol{x}_i, &\bar{y} % \overline{\boldsymbol{x}^2}&=\frac{1}{n}\sum_{i=1}^n\boldsymbol{x}_i\boldsymbol{x}_i^{\mathsf{T}},& &=\frac{1}{n}\sum_{i=1}^ny_i,& % \overline{\boldsymbol{x}y}&=\frac{1}{n}\sum_{i=1}^n\boldsymbol{x}_iy_i \end{align}
\(\boldsymbol{\hat{\beta}}\) が最小二乗推定量のとき以下が成立

\begin{equation} \bar{y} = (1,\boldsymbol{\bar{x}}^{\mathsf{T}})\boldsymbol{\hat{\beta}} \end{equation}

実習

R : 推定結果からの情報の取得

関数 lm() の出力には様々な情報が含まれる

#' lmの出力を引数とする関数の例
coef(lmの出力)         # 推定された回帰係数
fitted(lmの出力)       # あてはめ値
resid(lmの出力)        # 残差
model.frame(lmの出力)  # modelに必要な変数の抽出 (データフレーム)
model.matrix(lmの出力) # デザイン行列

R : 行列とベクトル

データフレーム以外の重要なデータ構造
- ベクトル (vector) : 1次元の配列
- 行列 (matrix) : 2次元の同じデータ型の配列

必要であれば明示的に変換できる

as.vector(データフレーム[列名]) # base::as.vector()
as_vector(データフレーム[列名]) # purrr::as_vector()
as.matrix(データフレーム) # base::as.matrix()
#' データフレームを行列に変換する場合は全て同じデータ型でなくてはならない

R : 行列とベクトルの計算

行列 \(A,B\) の積 \(AB\) およびベクトル \(a,b\) の内積 \(a\cdot b\)

A %*% B # 行列の大きさは適切である必要がある
a %*% b # ベクトルは同じ長さである必要がある

正方行列 \(A\) の逆行列 \(A^{-1}\)

solve(A) # 他にもいくつか関数はある

\(X^{\mathsf{T}}Y\) および \(X^{\mathsf{T}}X\) の計算

crossprod(X, Y) # cross product の略
#' X: 行列 (またはベクトル)
#' Y: 行列 (またはベクトル)
crossprod(X) # 同じものを掛ける場合は引数は1つで良い

練習問題

前問の推定結果を用いて最小二乗推定量の性質を確認しなさい
- 推定された係数が正規方程式の解
  
  \begin{equation} \boldsymbol{\hat{\beta}} = (X^{\mathsf{T}}X)^{-1}X^{\mathsf{T}}\boldsymbol{y} \end{equation}
  
  となること
- あてはめ値と残差が直交すること
- 回帰式が標本平均を通ること

残差の分解

最小二乗推定量の残差

観測値と推定値 \(\boldsymbol{\hat{\beta}}\) による予測値の差

\begin{equation} \hat{\epsilon}_i= y_i-(\hat{\beta}_0+\hat{\beta}_1 x_{i1}+\dotsb+\hat{\beta}_px_{ip}) \quad (i=1,\dotsc,n) \end{equation}
- 誤差項 \(\epsilon_1,\dotsc,\epsilon_n\) の推定値
- 全てができるだけ小さいほど良い
- 予測値とは独立に偏りがないほど良い
残差ベクトル

\begin{equation} \boldsymbol{\hat{\epsilon}} =\boldsymbol{y}-\boldsymbol{\hat{y}} =(\hat{\epsilon}_1,\hat{\epsilon}_2,\dotsc,\hat{\epsilon}_n)^{\mathsf{T}} \end{equation}

平方和の分解

\(\bar{\boldsymbol{y}}=\bar{y}\boldsymbol{1}=(\bar{y},\bar{y},\dotsc,\bar{y})^{\mathsf{T}}\) : 標本平均のベクトル
いろいろなばらつき
- \(S_y=(\boldsymbol{y}-\bar{\boldsymbol{y}})^{\mathsf{T}} (\boldsymbol{y}-\bar{\boldsymbol{y}})\) : 目的変数のばらつき
- \(S_{\phantom{y}}=(\boldsymbol{y}-\boldsymbol{\hat{y}})^{\mathsf{T}} (\boldsymbol{y}-\boldsymbol{\hat{y}})\) : 残差のばらつき (\(\boldsymbol{\hat{\epsilon}}^{\mathsf{T}}\boldsymbol{\hat{\epsilon}}\))
- \(S_r=(\boldsymbol{\hat{y}}-\bar{\boldsymbol{y}})^{\mathsf{T}} (\boldsymbol{\hat{y}}-\bar{\boldsymbol{y}})\) : あてはめ値(回帰)のばらつき
3つのばらつき(平方和)の関係

\begin{equation} (\boldsymbol{y}-\bar{\boldsymbol{y}})^{\mathsf{T}} (\boldsymbol{y}-\bar{\boldsymbol{y}}) = (\boldsymbol{y}-\boldsymbol{\hat{y}})^{\mathsf{T}} (\boldsymbol{y}-\boldsymbol{\hat{y}})+ (\boldsymbol{\hat{y}}-\bar{\boldsymbol{y}})^{\mathsf{T}} (\boldsymbol{\hat{y}}-\bar{\boldsymbol{y}}) \end{equation}

\begin{equation} S_y=S+S_r \end{equation}

実習

練習問題

前問の結果を用いて残差の性質を確認しなさい
- 以下の分解が成り立つこと
  
  \begin{equation} (\boldsymbol{y}-\bar{\boldsymbol{y}})^{\mathsf{T}} (\boldsymbol{y}-\bar{\boldsymbol{y}}) = (\boldsymbol{y}-\boldsymbol{\hat{y}})^{\mathsf{T}} (\boldsymbol{y}-\boldsymbol{\hat{y}})+ (\boldsymbol{\hat{y}}-\bar{\boldsymbol{y}})^{\mathsf{T}} (\boldsymbol{\hat{y}}-\bar{\boldsymbol{y}}) \end{equation}
  
  \begin{equation} S_y=S+S_r \end{equation}

決定係数

回帰式の寄与

ばらつきの分解

\begin{equation} S_y\;\text{(目的変数)} =S\;\text{(残差)} +S_r\;\text{(あてはめ値)} \end{equation}
回帰式で説明できるばらつきの比率

\begin{equation} \text{(回帰式の寄与率)} = \frac{S_{r}}{S_{y}} = 1-\frac{S}{S_{y}} \end{equation}
回帰式のあてはまり具合を評価する代表的な指標

決定係数 (\(R^2\)値)

決定係数 (R-squared)

\begin{equation} R^2 = 1-\frac{\sum_{i=1}^n\hat{\epsilon}_i^2}{\sum_{i=1}^n(y_i-\bar{y})^2} \end{equation}
自由度調整済み決定係数 (adjusted R-squared)

\begin{equation} \bar{R}^2 = 1-\frac{\frac{1}{n{-}p{-}1}\sum_{i=1}^n\hat{\epsilon}_i^2} {\frac{1}{n{-}1}\sum_{i=1}^n(y_i-\bar{y})^2} \end{equation}
- 不偏分散で補正している

実習

練習問題

決定係数を用いてモデルの比較を行いなさい
- 東京の8月の気候データ
```
temp ~ solar
temp ~ solar + press
temp ~ solar + press + cloud
```
- 広告費と売上データ
```
sales ~ TV
sales ~ radio
sales ~ TV + radio
```

次回の予定

第1回 : 回帰モデルの考え方と推定
第2回 : モデルの評価
第3回 : モデルによる予測と発展的なモデル