検定

第11講 - 仮説の正当性をデータから検証する

(Press ? for help, n and p for next and previous slide)

村田昇

講義概要

検定
- 帰無仮説と対立仮説
- 棄却域
- \(p\) 値
平均の検定
分散の検定
平均の差の検定
分散の比の検定

検定とは

統計的仮説検定

ある現象・母集団に対して仮定された仮説の真偽をデータに基づいて統計的に検証する方法
薬の治験の例

新しい薬の効能が古い薬よりも優れていること(仮説)を薬の治験結果(データ)から検証したい
推定と大きく異なるのは，母集団の分布に対して何らかの仮説を考えるところ

検定の基本的手続き

仮説を立てる
仮説のもとで 検定統計量 が従う標本分布を調べる
実際のデータから検定統計量の値を計算する
計算された検定統計量の値が仮説が正しいときに十分高い確率で得られるかどうかを判断する

検定における仮説

帰無仮説

検定統計量の分布を予想するために立てる仮説
対立仮説

“帰無仮説が誤っているときに起こりうるシナリオ”として想定する仮説
- 慣習として帰無仮説を \(H_0\), 対立仮説を \(H_1\) で表す
- “帰無仮説を捨てて無に帰する”ことを期待する場合が多い

帰無仮説と対立仮説

薬の治験の例 (単純な場合)
- 帰無仮説 \(H_0\) : 新しい薬も古い薬も効能は同じ
- 対立仮説 \(H_1\) : 新しい薬と古い薬の効能は異なる
薬の治験の例 (新薬がより良いことを期待する場合)
- 帰無仮説 \(H_0\) : 新しい薬も古い薬も効能は同じ
- 対立仮説 \(H_1\) : 新しい薬の方が古い薬より効能が高い

検定の用語

帰無分布

帰無仮説が正しい場合に検定統計量が従う分布
棄却域

帰無仮説の下で統計量の取り得るべき範囲の外の領域
仮説検定
- 帰無仮説を棄却 : 帰無仮説は誤っていると判断すること
- 帰無仮説を受容 : 帰無仮説を積極的に棄却できないこと
検定の誤り
- 第一種過誤 : “正しい帰無仮説を棄却する”誤り
- 第二種過誤 : “誤った帰無仮説を受容する”誤り

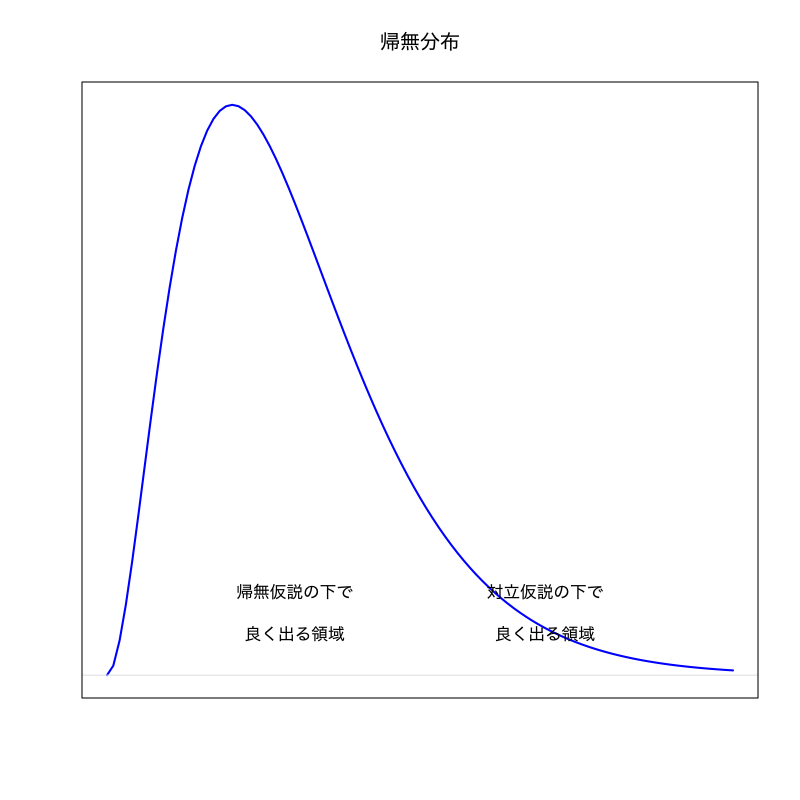
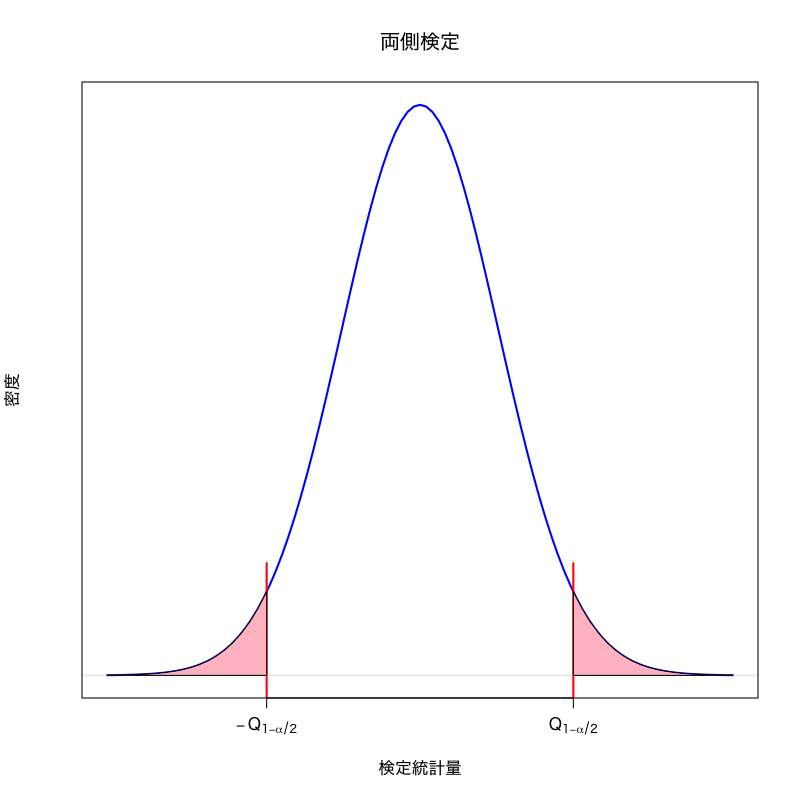
Figure 1: 検定の考え方

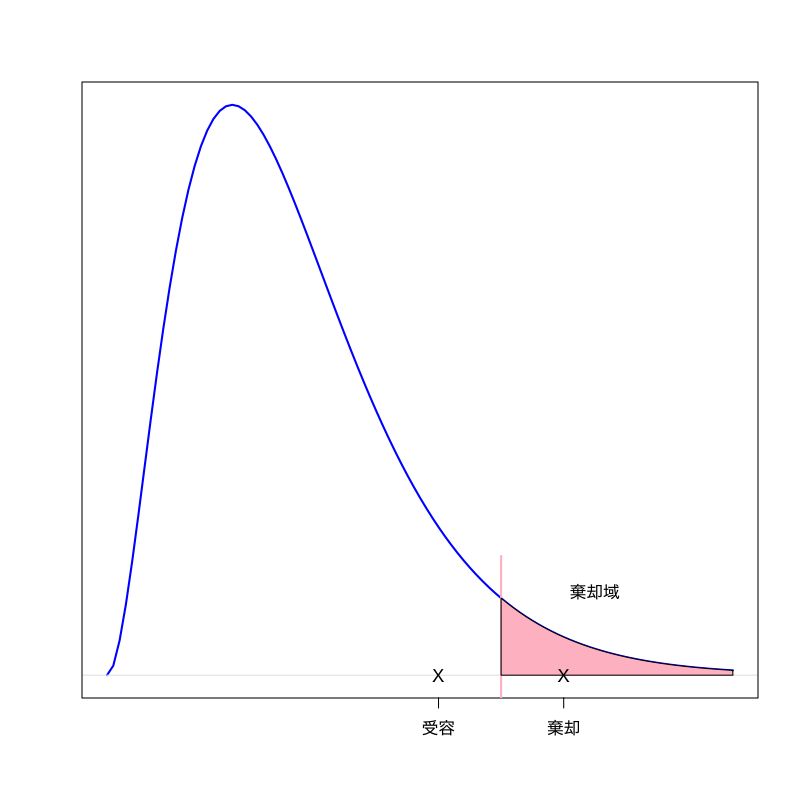
Figure 2: 棄却と受容

検定の設計指針

検定統計量 \(T\) に対して棄却域 \(R\) を設計
- サイズ : 第一種過誤が 起きる確率
  
  \begin{equation} \text{(サイズ)} =P(\text{\(T\) が\(R\)に含まれる}|\text{帰無仮説が正しい}) \end{equation}
- 検出力 : 第二種過誤が 起きない確率
  
  \begin{equation} \text{(検出力)} =P(\text{\(T\) が\(R\)に含まれる}|\text{対立仮説が正しい}) \end{equation}
有意水準

第一種過誤が起きる確率(サイズ)として許容する上限

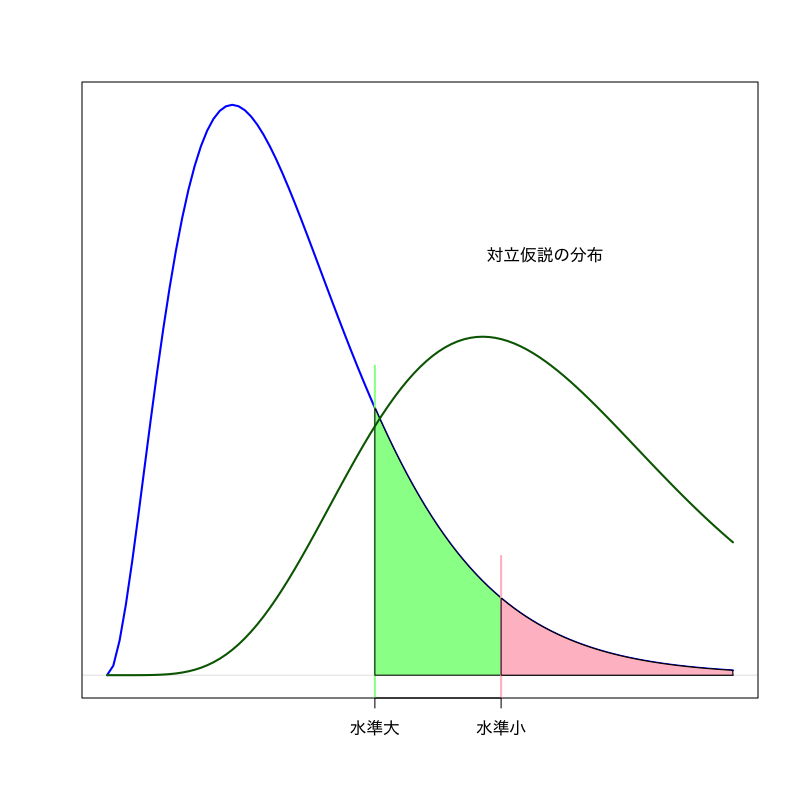
Figure 3: 検定の設計

棄却域の決め方

検定を構成する場合の一般的な戦略
棄却域 \(R_{\alpha}\) は以下のように設定する
- サイズを小さく (有意水準 \(\alpha\) 以下に) 抑える
- 可能な限り 検出力を大きく する
  
  \begin{align} P(T \in R_{\alpha}|\text{帰無仮説が正しい}) &\le\alpha\\ P(T \in R_{\alpha}|\text{対立仮説が正しい}) &\to\text{最大化} \end{align}
対立仮説によって棄却域の形は変わりうる

\(p\) 値 (有意確率)

帰無分布における検定統計量の評価

検定統計量の値が棄却域に含まれる有意水準の最小値を考える
\(p\) 値 (有意確率) : (検定統計量 \(T\), 棄却域 \(R_{\alpha}\))

\begin{equation} \text{(\(p\) 値)} =\min\{\alpha\in(0,1)|\text{\(T\) が\(R_{\alpha}\)に含まれる}\} \end{equation}
\(p\) 値が有意水準未満のときに帰無仮説を棄却する

検定に関する注意

帰無仮説の受容の意味

帰無仮説が正しいと仮定しても矛盾は生じない

帰無仮説の正しさを積極的に支持する結果ではない
第二種過誤

一般に第二種過誤の起こる確率については何ら仮定がないため，その確率は非常に大きい可能性がある

1標本正規母集団

1標本データに対する仮定

観測データは独立同分布な確率変数列

\begin{equation} X_1,X_2,\dotsc,X_n \end{equation}
\(X_{i}\) は平均 \(\mu\), 分散 \(\sigma^2\) の正規分布に従う
以下では平均 \(\mu\) および分散 \(\sigma^2\) に対する検定を説明

平均の検定

両側検定

\(\mu_0\) を既知の定数として，観測データを生成している分布の平均 \(\mu\) が \(\mu_0\) であるか否かを検定する
- 帰無仮説と対立仮説
  
  \begin{equation} H_0:\mu=\mu_0\quad\text{vs}\quad H_1:\mu\neq\mu_0. \end{equation}

考え方

標本平均 \(\bar{X}\) (推定量) が帰無仮説のもとでの真の平均 \(\mu_0\) とどの程度離れているかを検証
平均と分散の推定量を用いて検定統計量を構成
- 標本平均 (正規分布に従う)
  
  \begin{equation} \bar{X}=\frac{1}{n}\sum_{i=1}^nX_i \end{equation}
- 不偏分散 (\(\chi^2\) 分布に従う)
  
  \begin{equation} s^2=\frac{1}{n{-}1}\sum_{i=1}^n(X_i-\bar{X})^2 \end{equation}

Studentの \(t\) 検定

\begin{equation} \text{検定統計量 : } t=\frac{\sqrt{n}(\bar{X}-\mu_0)}{s} \end{equation}
- 帰無分布は自由度 \(n{-}1\) の \(t\) 分布
  (帰無仮説 \(H_0\) のもとでの検定統計量 \(t\) の分布)

\(t\) 分布

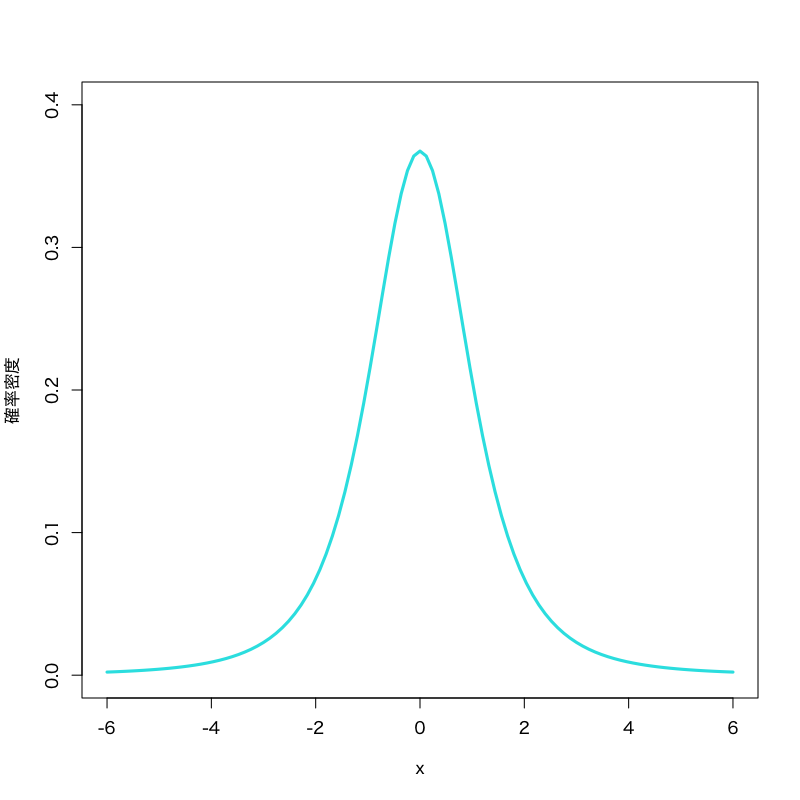
Figure 4: \(t\) 分布 (自由度\(3\))

見本空間 : \((-\infty,\infty)\)

母数 : 自由度 \(\nu\)

密度関数 :

\begin{equation} f(x)= \frac{\Gamma\left(\frac{\nu+1}{2}\right)} {\sqrt{\nu\pi}\;\Gamma\left(\frac{\nu}{2}\right)} \left(1+\frac{x^{2}}{\nu}\right)^{-\frac{1}{2}(\nu+1)} \end{equation}

備考 : 標準正規分布と自由度 \(\nu\) の \(\chi^{2}\) 分布に従う独立な確率変数の比に関する分布で，検定に利用される．

棄却域を用いる場合

有意水準を選択 : \(\alpha\in(0,1)\)
\(H_0\) の下で以下が成立

\begin{equation} P(|t|>t_{1{-}\alpha/2}(n{-}1))=\alpha \end{equation}
- \(t_{1{-}\alpha/2}(n{-}1)\) : 自由度 \(n{-}1\) の \(t\) 分布の \(1{-}\alpha/2\) 分位点
第一種過誤の上限が \(\alpha\) の棄却域

\begin{equation} R_{\alpha}= \left(-\infty,-t_{1{-}\alpha/2}(n{-}1)\right) \cup\left(t_{1{-}\alpha/2}(n{-}1),\infty\right) \end{equation}

データから検定統計量 \(t\) の値を計算
以下の場合，帰無仮説を棄却

\begin{equation} |t|>t_{1{-}\alpha/2}(n{-}1),\quad (t\in R_{\alpha}) \end{equation}

\(p\) 値を用いる場合

\(p\) 値を計算 ( \(f(x)\) : 自由度 \(n{-}1\) の \(t\) 分布の密度)

\begin{equation} \text{(\(p\) 値)} =2\int_{|t|}^\infty f(x)dx \end{equation}
\(p\) 値が \(\alpha\) 未満なら帰無仮説を棄却

\begin{align} |t|>t_{1{-}\alpha/2}(n{-}1) &\Leftrightarrow \int_{-\infty}^{|t|}f(x)dx> \int_{-\infty}^{t_{1{-}\alpha/2}(n{-}1)}f(x)dx=1{-}\alpha/2\\ &\Leftrightarrow \int_{|t|}^\infty f(x)dx < \alpha/2 \Leftrightarrow 2\int_{|t|}^\infty f(x)dx < \alpha \end{align}

対立仮説の違い

薬の治験例
観測データ \(X_1,X_2,\dotsc,X_n\) (\(n\) 人の被験者の治験結果) に対する仮説
- 古い薬(高価)と新しい薬(安価)の効能が変わらない (両側検定)
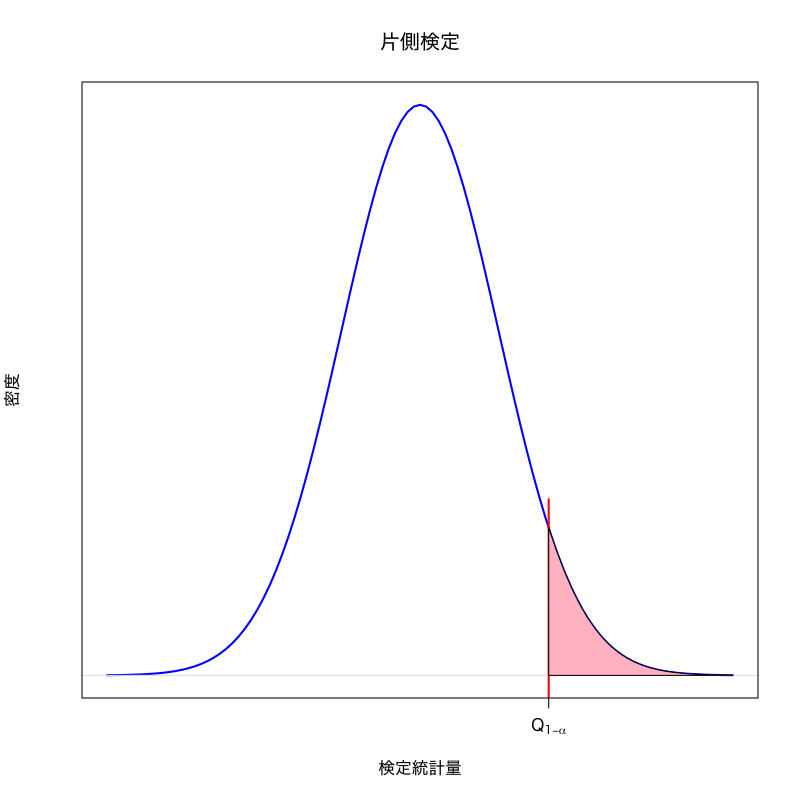
- 古い薬に比べて新しい薬の効能が改善した
対立仮説によって棄却域の形は変わりうる

平均の検定

右片側検定

\(\mu_0\) を既知の定数として，観測データを生成している分布の平均 \(\mu\) が \(\mu_0\) より大きいかを検定する
- 帰無仮説と対立仮説
  
  \begin{equation} H_0:\mu=\mu_0\quad\text{vs}\quad H_1:\mu>\mu_0. \end{equation}
- 検定統計量の標本分布
  - 帰無仮説は同一なので検定統計量 \(t\) の帰無分布も同一となる
  - 対立仮説の下で \(t\) の値は正の方向に大きくなると期待される
- 棄却域 “\(t>c\)” (\(c\) は正の数) を考えるのが自然

棄却域を用いる場合

有意水準を選択 : \(\alpha\in(0,1)\)
\(H_0\) の下で以下が成立

\begin{equation} P(t>t_{1{-}\alpha}(n{-}1))=\alpha \end{equation}
- \(t_{1{-}\alpha}(n{-}1)\): 自由度 \(n{-}1\) の \(t\) 分布の \(1{-}\alpha\) 分位点
第一種過誤の上限が \(\alpha\) の棄却域

\begin{equation} R_{\alpha}= \left(t_{1{-}\alpha}(n{-}1),\infty\right) \end{equation}

データから検定統計量 \(t\) の値を計算
以下の場合，帰無仮説を棄却

\begin{equation} t>t_{1{-}\alpha}(n{-}1) \end{equation}

\(p\) 値を用いる場合

\(p\) 値を計算 ( \(f(x)\):自由度 \(n{-}1\) の \(t\) 分布の密度)

\begin{equation} \text{(\(p\) 値)}= \int_{t}^\infty f(x)dx \end{equation}
\(p\) 値が \(\alpha\) 未満なら帰無仮説を棄却

平均の検定

左片側検定
- 反対向きの対立仮説 \(\mu < \mu_0\) を考えた検定
  
  \begin{equation} H_0:\mu=\mu_0\quad\text{vs}\quad H_1:\mu < \mu_0. \end{equation}
- 以下の場合，帰無仮説を棄却
  
  \begin{equation} t < t_{\alpha}(n{-}1) \quad \text{(自由度 \(n{-}1\) の \(t\) 分布の \(\alpha\) 分位点)} \end{equation}
- 以下の \(p\) 値が \(\alpha\) 未満なら帰無仮説を棄却
  
  \begin{equation} \text{(\(p\) 値)} =\int_{-\infty}^t f(x)dx \end{equation}

両側検定と片側検定

棄却域の形による分類
- 両側検定
  
  ある定数 \(a < b\) を用いて \(\text{(棄却域)}=(-\infty,a)\cup(b,\infty)\)
- 右片側検定
  
  ある定数 \(a\) を用いて \(\text{(棄却域)}=(a,\infty)\)
- 左片側検定
  
  ある定数 \(a\) を用いて \(\text{(棄却域)}=(-\infty,a)\)
  - 右片側検定と左片側検定を合わせて 片側検定 と呼ぶ

平均の検定の場合
- 対立仮説を \(H_{1}:\mu\neq\mu_{0}\) にとった場合は両側検定
- 対立仮説を \(H_{1}:\mu>\mu_{0}\) にとった場合は右片側検定
- 対立仮説を \(H_{1}:\mu<\mu_{0}\) にとった場合は左片側検定

\(t\) 検定の関数

使い方

t.test(x, # 1標本の場合
       alternative = c("two.sided", "less", "greater"),
       mu = 0, conf.level = 0.95, ...)
#' x : ベクトル． 
#' alternative: 対立仮説 (両側，左片側，右片側)
#' mu: 検定対象の平均値
#' conf.level: 信頼区間の水準 (点推定・区間推定も行ってくれる)
#' ...: 他のオプション．詳細は help(t.test) を参照

実習

練習問題

適当な正規乱数を用いてMonte-Carlo実験を考案し， \(t\) 検定の過誤について調べなさい．

#' 例えば適当な数値を指定して以下のような実験を行えばよい
mc_trial <- function(n){ 
  result <- t.test(rnorm(n,mean = mu0,sd = sd0), mu = mu0)
  return(result$p.value)}
mc_data <- replicate(mc, mc_trial(n))
table(mc_data < alpha)/mc # alpha以下のデータの数を調べる
#' 上記はp値の性質を調べる場合であるが，t統計量についても同様に調べることができる

練習問題

ある番組の視聴率が2桁に達したかどうか知るために \(n\) 人にその番組を観たかどうか確認する．

\begin{equation} X_{i}= \begin{cases} 1,&\text{番組を観た}\\ 0,&\text{番組を観ていない} \end{cases},\; i=1,2,\dotsc,n \end{equation}

これを用いた検定を考えてみよ．
```
#' Xの生成は例えば mu1 を真の視聴率として以下のようにすればよい
x <- sample(0:1, n, replace = TRUE, prob = c(1-mu1,mu1))
#' n 人分の視聴結果 {1,0} のベクトルが得られる
```
- ヒント : \(X\) は正規分布には従わないが， \(n\) が大きければ標本平均 \(\bar{X}\) は正規分布で十分良く近似できる

分散の検定

両側検定

\(\sigma_0^2\) を既知の定数として，観測データを生成している分布の分散 \(\sigma^2\) が \(\sigma_0^2\) であるか否かを検定する
- 帰無仮説と対立仮説
  
  \begin{equation} H_0:\sigma^2=\sigma_0^2\quad\text{vs}\quad H_1:\sigma^2\neq\sigma_0^2 \end{equation}

考え方

不偏分散 \(s^2\) が真の分散 \(\sigma_{0}^{2}\) とどの程度離れているかを検証
分散の推定量の性質を用いて検定統計量を構成
- 不偏分散 (\(\chi^2\) 分布に従う)
  
  \begin{equation} s^2=\frac{1}{n{-}1}\sum_{i=1}^n(X_i-\bar{X})^2 \end{equation}

\(\chi^2\) 検定

\begin{equation} \text{検定統計量 : } \chi^2=\frac{(n{-}1)s^2}{\sigma_0^2} \end{equation}
- 帰無分布は自由度 \(n{-}1\) の \(\chi^2\) 分布

\(\chi^{2}\) 分布

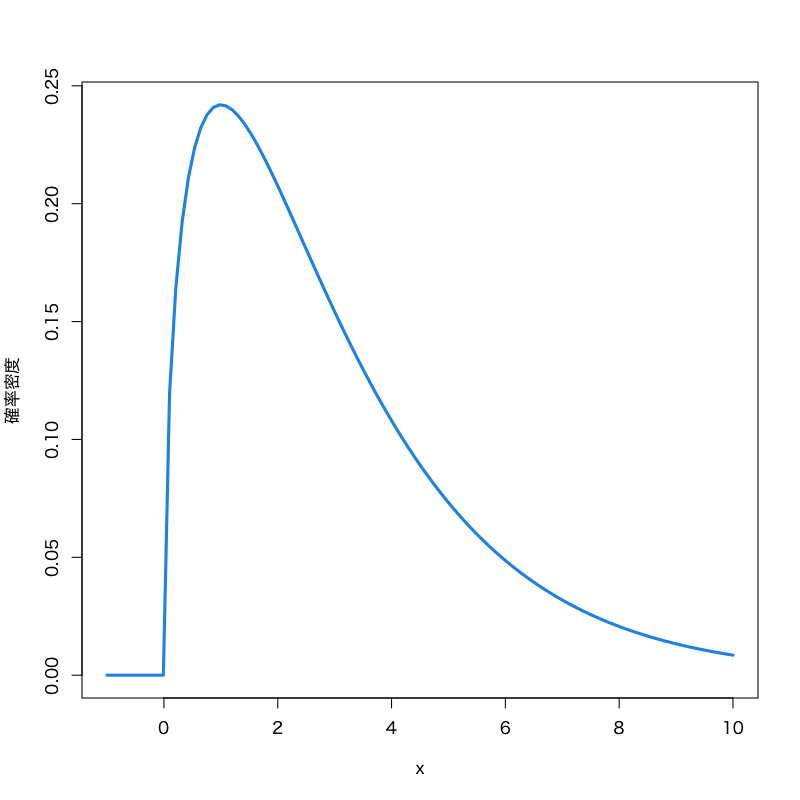
Figure 5: \(\chi^{2}\) 分布 (自由度\(3\))

見本空間 : \([0,\infty)\)

母数 : 自由度 \(\nu\)

密度関数 :

\begin{align} f(x)=& \frac{1}{2^{\nu/2}\Gamma(\frac{\nu}{2})}x^{\nu/2-1}e^{-x/2}\\ &\Gamma(z)=\int_0^\infty e^{-t}t^{z-1}dt \end{align}

備考 : \(\nu\) 個の標準正規分布に従う確率変数の2乗和の分布で，検定に利用される．

棄却域を用いる場合

有意水準を選択 : \(\alpha\in(0,1)\)
\(H_0\) の下で以下が成立

\begin{equation} P(\chi^2 < \chi^2_{\alpha/2}(n{-}1) \text{ または }\chi^2>\chi^2_{1{-}\alpha/2}(n{-}1)) =\alpha \end{equation}
- \(\chi^2_{\alpha/2}(n{-}1)\): 自由度 \(n{-}1\) の \(\chi^2\) 分布の \(\alpha/2\) 分位点
- \(\chi^2_{1{-}\alpha/2}(n{-}1)\): 自由度 \(n{-}1\) の \(\chi^2\) 分布の \(1{-}\alpha/2\) 分位点
第一種過誤の上限が \(\alpha\) となる棄却域

\begin{equation} R_{\alpha}= \left(-\infty,\chi^2_{\alpha/2}(n{-}1)\right) \cup\left(\chi^2_{1{-}\alpha/2}(n{-}1),\infty\right) \end{equation}

データから検定統計量 \(\chi^2\) の値を計算
以下の場合，帰無仮説を棄却

\begin{equation} \chi^2 < \chi^2_{\alpha/2}(n{-}1) \text{ または }\chi^2>\chi^2_{1{-}\alpha/2}(n{-}1) \end{equation}

\(p\) 値を用いる場合

\(p\) 値を計算 ( \(f(x)\): 自由度 \(n{-}1\) の \(\chi^2\) 分布の密度)

\begin{equation} \text{(\(p\) 値)} =2\min\left\{\int_0^{\chi^2}f(x)dx,\int_{\chi^2}^\infty f(x)dx\right\} \end{equation}
\(p\) 値が \(\alpha\) 未満なら帰無仮説を棄却

片側検定

対立仮説が片側 (右側対立仮説) の場合
- 帰無仮説と対立仮説
  
  \begin{equation}%\label{two-side} H_0:\sigma^2=\sigma_0^2\quad \text{vs}\quad H_1:\sigma^2>\sigma_0^2 \end{equation}
左側対立仮説 \(H_1:\sigma^2 < \sigma_0^2\) も以下の議論は同様

棄却域を用いる場合

自由度 \(n{-}1\) の \(\chi^2\) 分布の \(1{-}\alpha\) 分位点 : \(\chi^2_{1{-}\alpha}(n{-}1)\)
以下の場合，帰無仮説を棄却

\begin{equation} \chi^2>\chi^2_{1{-}\alpha}(n{-}1) \end{equation}

\(p\) 値を用いる場合

\(p\) 値を計算 ( \(f(x)\):自由度 \(n{-}1\) の \(\chi^2\) 分布の密度)

\begin{equation} \text{(\(p\) 値)} =\int_{\chi^2}^\infty f(x)dx \end{equation}
\(p\) 値が \(\alpha\) 未満なら帰無仮説を棄却

\(\chi^2\) 検定の計算

関数 chisq.test はあるが目的が違うので注意 (適合度検定・独立性検定)

\(\chi^2\) 分布に関する関数を用いて直接計算することができる

x # 観測データ
sigma0 # 帰無仮説で用いる標準偏差
n <- length(x) # データ数
chi2 <- (n-1)*var(x)/sigma0^2 # 検定統計量を計算する
p0 <- pchisq(chi2, df=n-1)
2*min(p0, 1-p0) # p値 (両側検定の場合)

実習

練習問題

東京の気象データの気温の項目を用いて， 6月の気温の分散が，月毎に計算した気温の分散の平均値より大きいかどうか検定せよ．

tw_data <- read_csv("data/tokyo_weather.csv") 
#' 月毎の気温の分散は以下で計算できる
tw_data |> group_by(month) |> summarize(var(temp))
#' この平均値は以下のように計算される
tw_data |> group_by(month) |>
  summarize(var(temp)) |> pull(`var(temp)`) |> mean()

2標本正規母集団

2標本データに対する仮定

2種類の観測データ

\begin{align} &X_1,X_2,\dotsc,X_m\\ &Y_1,Y_2,\dotsc,Y_n \end{align}
3つの条件を仮定
- \(X_1,X_2,\dotsc,X_m,Y_1,Y_2,\dotsc,Y_n\) は独立な確率変数列
- \(X_1,\dotsc,X_m\) は同分布で平均 \(\mu_1\) 分散 \(\sigma_1^2\) の正規分布に従う
- \(Y_1,\dotsc,Y_n\) は同分布で平均 \(\mu_2\) 分散 \(\sigma_2^2\) の正規分布に従う
両者の平均や分散が一致するかどうかを検定する

平均の差の検定

両側検定

2種類のデータの平均が等しいか否かを検定する
- 帰無仮説と対立仮説
  
  \begin{equation}%\label{mean-equal} H_0:\mu_1=\mu_2\quad\text{vs}\quad H_1:\mu_1\neq\mu_2 \end{equation}
Behrens-Fisher問題
- 正確かつ適切な検定を導出することは難しい
Welch(またはSatterthwaite)の近似法
- \(\chi^2\) 分布に従う独立確率変数列の一次結合の分布を， 1つの \(\chi^2\) 分布に従う確率変数の定数倍の分布で近似する方法
- 平均と分散が元の確率変数と一致するように近似

考え方

\(X_1,\dotsc,X_m\) および \(Y_1,\dotsc,Y_m\) の不偏分散 : \(s_1^2\),\(s_2^2\)

\begin{equation} s_1^2=\frac{1}{m{-}1}\sum_{i=1}^m(X_i-\bar{X})^2,\quad s_2^2=\frac{1}{n{-}1}\sum_{i=1}^n(Y_i-\bar{Y})^2. \end{equation}
標本平均と不偏分散の性質
- \(\bar{X}-\bar{Y},s_1^2,s_2^2\) は独立となる
- \((m{-}1)s_1^2/\sigma_1^2\) は自由度 \(m{-}1\) の \(\chi^2\) 分布に従う
- \((n{-}1)s_2^2/\sigma_2^2\) は自由度 \(n{-}1\) の \(\chi^2\) 分布に従う

Welchの近似法

詳細は資料を参照
確率変数 \(s_1^2/m+s_2^2/n\) の分布を \(c\chi^2_\nu\) の分布で近似
\(\chi^2_\nu\) は自由度 \(\nu\) の \(\chi^2\) 分布に従う確率変数

\begin{equation} c=\frac{\frac{(\sigma_1^2/m)^2}{m{-}1}+ \frac{(\sigma_2^2/n)^2}{n{-}1}}{\sigma_1^2/m+\sigma_2^2/n},\quad \nu=\frac{(\sigma_1^2/m+\sigma_2^2/n)^2}{\frac{(\sigma_1^2/m)^2}{m{-}1}+ \frac{(\sigma_2^2/n)^2}{n{-}1}} \end{equation}
- 平均と分散を合わせる

検定統計量の近似

\begin{equation} t=\frac{\bar{X}-\bar{Y}}{\sqrt{s_1^2/m+s_2^2/n}} \simeq\frac{\bar{X}-\bar{Y}}{\sqrt{c\chi^2_\nu}} \end{equation}
- \(\bar{X}-\bar{Y},s_1^2/m+s_2^2/n\) は独立
- \(\bar{X}-\bar{Y},c\chi^2_\nu\) も独立と考える
- \(t\) の分布は \((\bar{X}-\bar{Y})/\sqrt{c\chi^2_\nu}\) で近似できる

データの正規性から以下は標準正規分布に従う

\begin{equation} \frac{(\bar{X}-\bar{Y})-(\mu_1{-}\mu_2)} {\sqrt{\sigma_1^2/m+\sigma_2^2/n}} \sim \mathcal{N}(0,1) \end{equation}
\(H_0\) の下で以下は自由度 \(\nu\) の \(t\) 分布に従う

\begin{equation} t\simeq \frac{\bar{X}-\bar{Y}}{\sqrt{c\chi^2_\nu}} =\frac{(\bar{X}-\bar{Y})/\sqrt{\sigma_1^2/m+\sigma_2^2/n}} {\sqrt{\frac{c}{\sigma_1^2/m+\sigma_2^2/n}\chi^2_\nu}} \end{equation}

検定統計量 \(t\) の帰無分布は自由度 \(\nu\) の \(t\) 分布で近似できる
Welchの \(t\) 検定

\(\nu\) は未知の分散 \(\sigma_1^2,\sigma_2^2\) を含むので不偏推定量 \(s_1^2,s_2^2\) で代用し，自由度 \(\hat{\nu}\) は次式を用いる．

\begin{align} \text{検定統計量 : } &t=\frac{\bar{X}-\bar{Y}}{\sqrt{s_1^2/m+s_2^2/n}}\\ \text{自由度 : } &\hat{\nu} =\frac{(s_1^2/m+s_2^2/n)^2} {\frac{(s_1^2/m)^2}{m{-}1}+\frac{(s_2^2/n)^2}{n{-}1}} \end{align}

棄却域を用いる場合

有意水準を選択 : \(\alpha\in(0,1)\)
棄却域

\begin{equation} \left(-\infty,-t_{1{-}\alpha/2}(\hat{\nu})\right) \cup\left(t_{1{-}\alpha/2}(\hat{\nu}),\infty\right) \end{equation}
- \(t_{1{-}\alpha/2}(\hat{\nu})\) : 自由度 \(\hat{\nu}\) の \(t\) 分布の \(1{-}\alpha/2\) 分位点

検定統計量 \(t\) の値を計算
以下の場合は帰無仮説を棄却

\begin{equation} |t|>t_{1{-}\alpha/2}(\hat{\nu}) \end{equation}
- \(p\) 値の計算や片側対立仮説への対応は前と同様

対応がある場合の平均の差の検定

対応がある観測データの平均の差の検定では 2種類のデータ間の自然な対応を考慮することがある
薬の投薬の例
- 2種類の薬の効能を比較するために被験者に両方の薬を投与
- 被験者 \(i\) にそれぞれの薬を投与した場合の治験結果: \(X_i,Y_i\)
- \(X_i\) と \(Y_i\) には“同一の被験者に対する治験結果”という意味で対応がある
- “対応がある観測値の差の平均が0” という帰無仮説を考える
- \(Z_i=X_i-Y_i\) \((i=1,\dotsc,n)\) として， \(Z_1,\dotsc,Z_n\) の平均が0か否かを検定すれば良い

\(t\) 検定の計算

使い方

t.test(x, y = NULL, # 2標本の場合
       alternative = c("two.sided", "less", "greater"),
       mu = 0, paired = FALSE, var.equal = FALSE,
       conf.level = 0.95, ...)
#' x,y: ベクトル．2標本の場合はyを指定する
#' alternative: 対立仮説 (両側，左片側，右片側)
#' mu: 検定対象の平均値
#' paired: 対応ありの場合は TRUE
#' var.equal: 2標本の分散を同じとして良い場合は TRUE

実習

練習問題

東京の気象データの気温の項目を用いて， 7月と8月の気温の平均が同じかどうか検定しなさい．
他の項目や自身の集めたデータでも試してみよ．

分散の比の検定

両側検定

2種類のデータの分散が等しいか否かを検定する
- 帰無仮説と対立仮説
  
  \begin{equation} H_0:\sigma_1^2=\sigma_2^2\quad\text{vs}\quad H_1:\sigma_1^2\neq\sigma_2^2 \end{equation}

考え方

\(X_1,\dotsc,X_m\) および \(Y_1,\dotsc,Y_n\) の不偏分散: \(s_1^2\), \(s_2^2\)
- このとき \(s_1^2,s_2^2\) は独立 :
  - \((m{-}1)s_1^2/\sigma_1^2\) 自由度 \(m{-}1\) の \(\chi^2\) 分布に従う
  - \((n{-}1)s_2^2/\sigma_2^2\) は自由度 \(n{-}1\) の \(\chi^2\) 分布に従う
\(F\) 検定

\begin{equation} \text{検定統計量 : } F=\frac{s_1^2}{s_2^2} \end{equation}
- 帰無分布は自由度 \(m{-}1,n{-}1\) の \(F\) 分布

\(F\) 分布

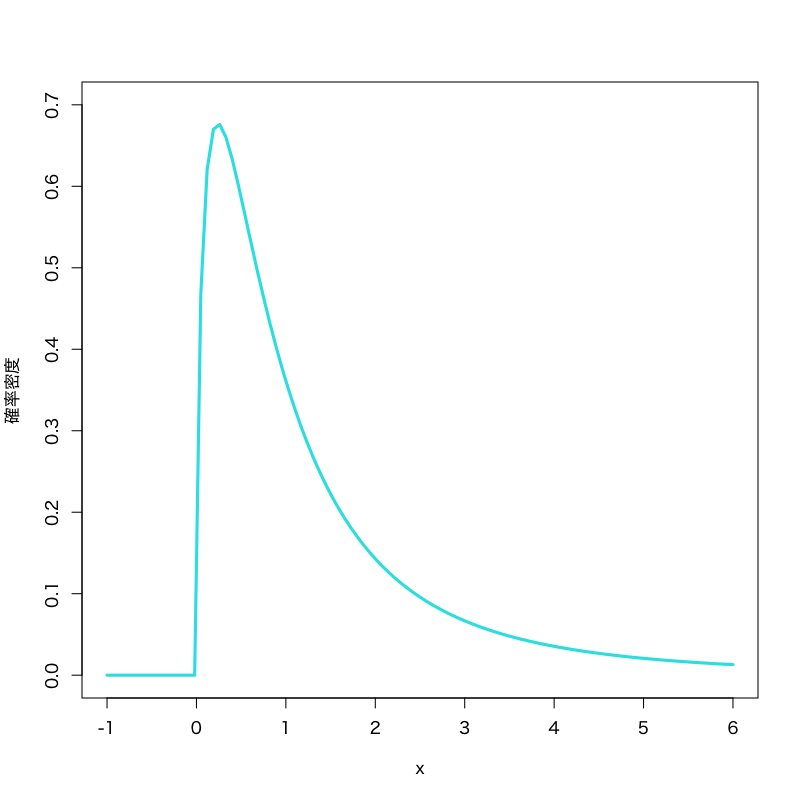
Figure 6: \(F\) 分布 (自由度\(3,5\))

標本空間: \([0,\infty)\)

母数: 自由度 \(\nu_{1},\nu_{2}\)

密度関数:

\begin{equation} f(x) = \frac{(\nu_{1}/\nu_{2})^{\nu_{1}/2}}{B(\nu_{1}/2,\nu_{2}/2)} \frac{x^{\nu_{1}/2-1}}{(1+\nu_{1}x/\nu_{2})^{(\nu_{1}+\nu_{2})/2}} \end{equation}

備考 : 自由度 \(k_{1},k_{2}\) の \(\chi^2\) 分布に従う独立な確率変数の比の分布で，分散の検定に利用される．

棄却域を用いる場合

有意水準を選択 : \(\alpha\in(0,1)\)
\(H_0\) の下では以下が成立

\begin{equation} P(F < F_{\alpha/2}(m{-}1,n{-}1) \text{ または }F > F_{1{-}\alpha/2}(m{-}1,n{-}1))=\alpha \end{equation}
- \(F_{\alpha/2}(m{-}1,n{-}1)\): 自由度 \(m{-}1,n{-}1\) の \(F\) 分布の \(\alpha/2\) 分位点
- \(F_{1{-}\alpha/2}(m{-}1,n{-}1)\): 自由度 \(m{-}1,n{-}1\) の \(F\) 分布の \(1{-}\alpha/2\) 分位点
第一種過誤の上限が \(\alpha\) の棄却域

\begin{equation} R_{\alpha}= \left(-\infty,F_{\alpha/2}(m{-}1,n{-}1)\right) \cup\left(F_{1{-}\alpha/2}(m{-}1,n{-}1),\infty\right) \end{equation}

データから検定統計量 \(F\) の値を計算
以下の場合，帰無仮説を棄却

\begin{equation} F < F_{\alpha/2}(m{-}1,n{-}1) \text{ または }F>F_{1{-}\alpha/2}(m{-}1,n{-}1) \end{equation}
- \(p\) 値の計算や片側対立仮説への対応は前と同様

\(F\) 検定の計算

使い方

var.test(x, y, ratio = 1,
         alternative = c("two.sided", "less", "greater"),
         conf.level = 0.95, ...)
#' x,y: ベクトル． 
#' ratio: 検定する比率(1は同じかどうか)
#' alternative: 対立仮説 (両側，左片側，右片側)
#' conf.level: 信頼区間の水準 (点推定・区間推定も行ってくれる)

演習

練習問題

東京の気象データの気温の項目を用いて， 3月と6月の気温の分散が同じかどうか検定しなさい．
他の項目や自身の集めたデータでも試してみよ．

次回の予定

分散分析とは
一元配置
- 一元配置のモデル
- 検定の構成
二元配置
- 二元配置のモデル
- 検定の構成