標本化定理

前回のおさらい

フィルタ

• 定義

  入力 \(f(t)\) を変換して出力 \(g(t)\) を生成する機構

• 線形性

  入力の線形結合がそのまま出力に反映される性質

• 時不変性

  入力の時刻がずれた場合，出力も同じだけずれる性質

線形時不変フィルタの数学的表現

• フィルタの積分表現

  \begin{equation} g(t)=\int_{-\infty}^{\infty} f(s)h(t{-}s)ds \end{equation}

  \(h\) : インパルス応答 = フィルタの表現

Fourier変換による表現

• 時間領域では畳み込み積分

  \begin{equation} g(t) =\int_{-\infty}^{\infty}h(t-s)f(s)ds = h{*}f(t) \end{equation}

• 周波数領域では関数の積

  \begin{equation} \hat{g}(\omega) = \sqrt{2\pi}\cdot\hat{h}(\omega)\cdot\hat{f}(\omega) \end{equation}

インパルス応答

• インパルス応答

  \begin{equation} h(t) =\int_{-\infty}^{\infty}\delta(s)h(t-s)ds \end{equation}

• \(h(t)\) はフィルタに \(\delta(t)\) を入力した時の出力
• 物理的には 面積1 (\(\Delta \times 1/\Delta\)) の矩形波に対する出力を 時間幅 \(\Delta\to0\) としたときの波形

ローパスフィルタ(RC回路)

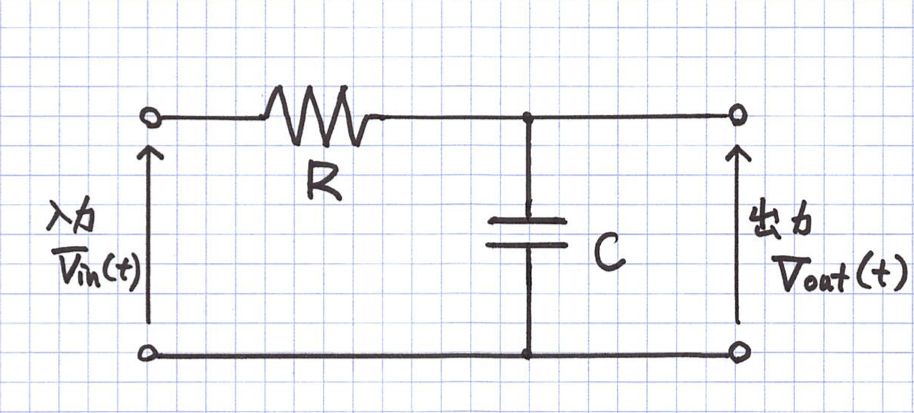
入出力の関係

• 時間領域

  \begin{equation} V_{in}(t) =CR\frac{d}{dt}V_{out}(t) +V_{out}(t) \end{equation}

• 周波数領域

  \begin{equation} \hat{V}_{in}(\omega) =i\omega CR\hat{V}_{out}(\omega) +\hat{V}_{out}(\omega) \end{equation}

  \begin{equation} \hat{V}_{out}(\omega) = \frac{1}{i\omega CR+1} \hat{V}_{in}(\omega) \end{equation}

インパルス応答 (逆 Fourier 変換)

• フィルタの Fourier 変換

  \begin{equation} \hat{h}(\omega) =\frac{1}{\sqrt{2\pi}i\omega CR+1} =\frac{1}{\sqrt{2\pi}iCR}\frac{1}{\omega -i/CR} \end{equation}

• 逆 Fourier 変換

  \begin{equation} \mathcal{F}^{-1}[\hat{h}](t) = h(t) = \begin{cases} 0,&t<0\\ \frac{1}{CR}e^{-\frac{t}{CR}},&t>0 \end{cases} \end{equation}

インパルス応答 (矩形波の極限)

• 矩形波の出力

  \begin{equation} V_{out}(t) = \begin{cases} 0,&t \le 0\\ \frac{1}{\Delta}(1-e^{-\frac{t}{CR}}),&0 < t\le\Delta\\ \frac{1}{\Delta}(e^{\frac{\Delta}{CR}}-1)e^{-\frac{t}{CR}},&\Delta< t \end{cases} \end{equation}

• \(\Delta\to 0\)

  \begin{equation} h(t) = \lim_{\Delta\to0}V_{out}(t) = \begin{cases} 0,&t\le0\\ \frac{1}{CR}e^{-\frac{t}{CR}},&t>0 \end{cases} \end{equation}

演習

練習問題

• 周期 \(2\pi\) の Fourier 級数展開の基底(正規直交系)を

  \begin{equation} \phi_{n}(t)=\frac{1}{\sqrt{2\pi}}e^{int} \end{equation}

  としたとき， 周期 \(2\pi\cdot 2B\) の基底は

  \begin{equation} \psi_{n}(t) = a\cdot \phi_{n}\left(b t\right) \end{equation}

  で構成することができる．\(a\) と \(b\) を求めよ．

デジタル信号処理

デジタル信号処理

• 計算機で信号を扱うための方法論
• 処理の流れ
  • アナログ信号をデジタル信号に変換 (A/D変換)
  • 計算機上でデジタル信号を処理
  • デジタル信号をアナログ信号に変換 (D/A変換)

計算機によるデータ処理

• アナログ信号は扱えない
  • 連続時間に対応していない
  • 連続値を正確に記録できない
• 信号の表現
  • 離散時間(クロックがある)
  • 0-1ベクトル (有限個の値)

アナログとデジタル

• アナログ
  • 連続的な量 (時間，振幅)
  • 雑音の影響を受けやすい
  • 物理的な保存や複製において劣化が生じる
• デジタル
  • 離散的な量 (時間，振幅)
  • 標本化と量子化による近似
  • 電子的に保存や複製が劣化なく行える

標本化と量子化

• デジタル信号に変換するための離散化 (discretization)
  • 標本化 (sampling) : 時間の離散化
  • 量子化 (quantization) : 数値の離散化
• 量子化は計算機で扱う数値の丸め誤差の問題
  (この講義では扱わない)

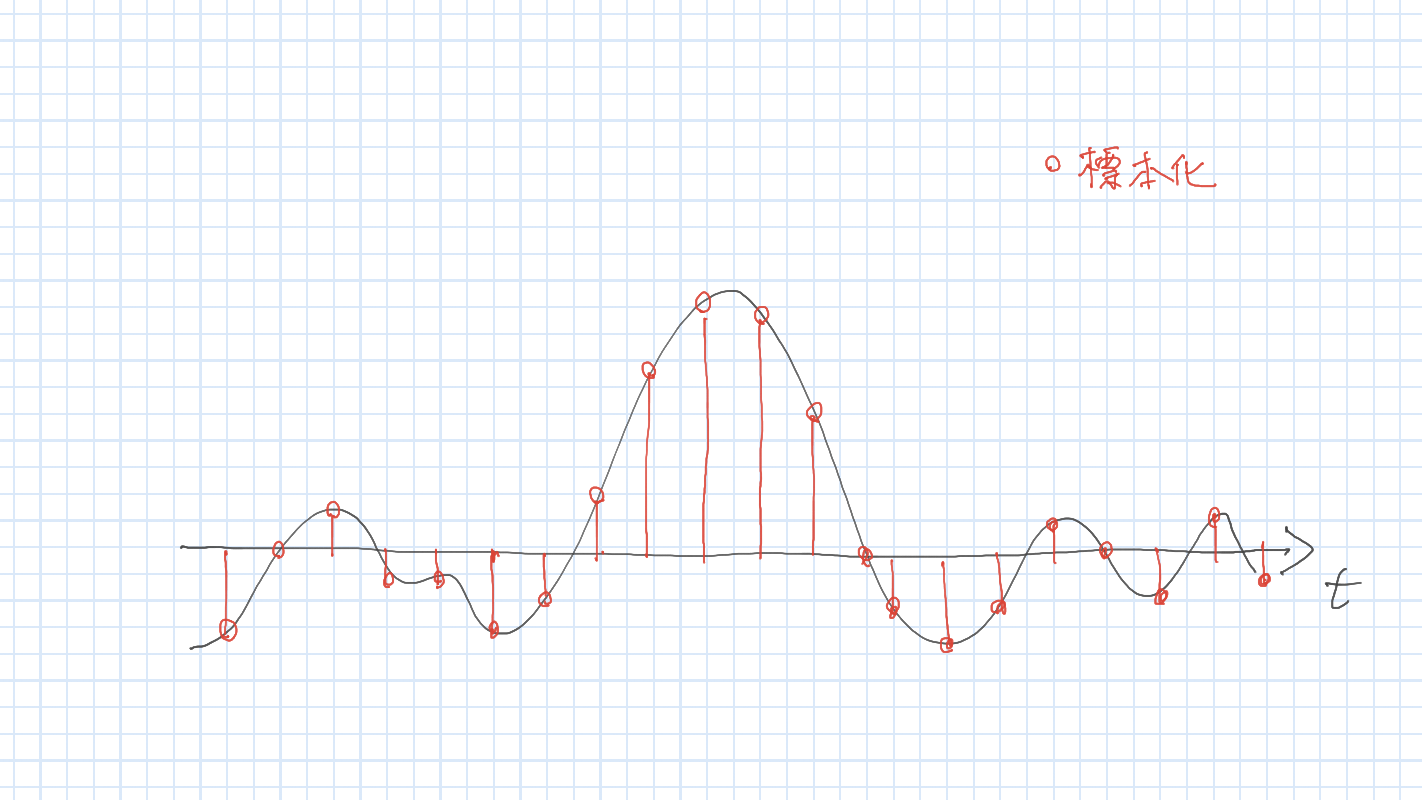
標本化における疑問

• 標本化 : 明らかに情報は落ちている
  • 離散データから連続データを再構成することはできるのか？
  • 再構成することができるのであれば，その条件は何か？

標本化定理

標本化定理

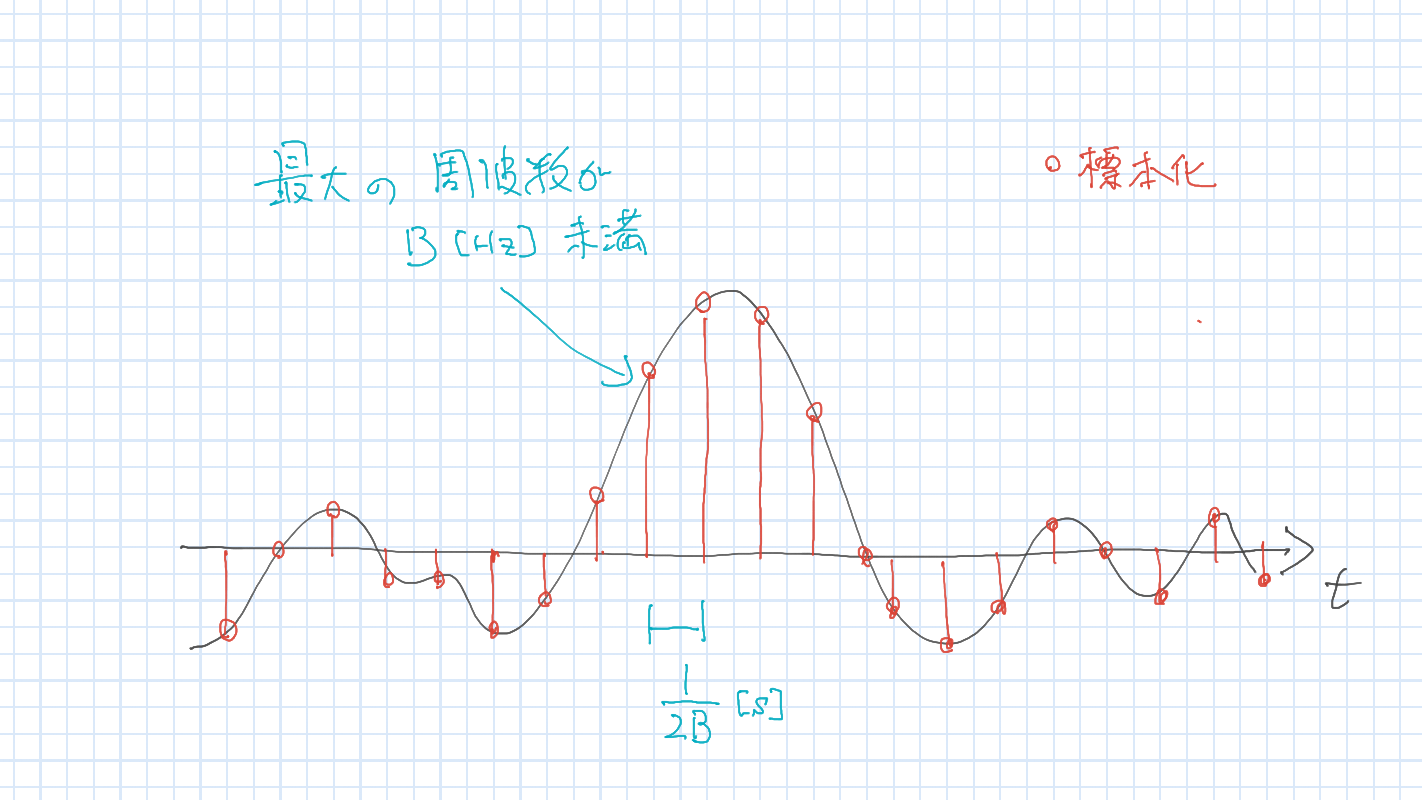
• 定理

  信号 \(f(t)\) が \(B\,[\mathrm{Hz}]\) 未満の周波数しか含んでいないなら， \(1/2B\,[s]\) ごとのサンプル点を用いて元の信号は完全に求められる．

• 定理の呼び名は色々ある (同時期に独立に発見)
  • Shannon の標本化定理
  • Nyquist-Shannon の標本化定理
  • Nyquist-Shannon-Kotelnikov の標本化定理
  • Whittaker-Shannon-Kotelnikov の標本化定理
  • Whittaker-Nyquist-Shannon-Kotelnikov の標本化定理
  • 染谷の標本化定理

• 用語
  • 1秒間に取るサンプル数 \(f_{s}\,[\mathrm{Hz}]\):
    サンプリング周波数 (sampling frequency)
  • 再構成に必要なサンプリング周波数の下限 \(2B\,[\mathrm{Hz}]\):
    Nyquist レート (Nyquist rate)
  • 信号に含まれる周波数の上限 \(B\,[\mathrm{Hz}]\):
    Nyquist 周波数 (Nyquist frequency)

演習

練習問題

• 以下の積分

  \begin{equation} \frac{1}{2\pi\cdot 2B}\int_{-2\pi B}^{2\pi B} e^{i\left(t+\frac{n}{2B}\right)\omega}d\omega \end{equation}

  を計算しなさい．

定理の証明と注意

標本化定理の証明

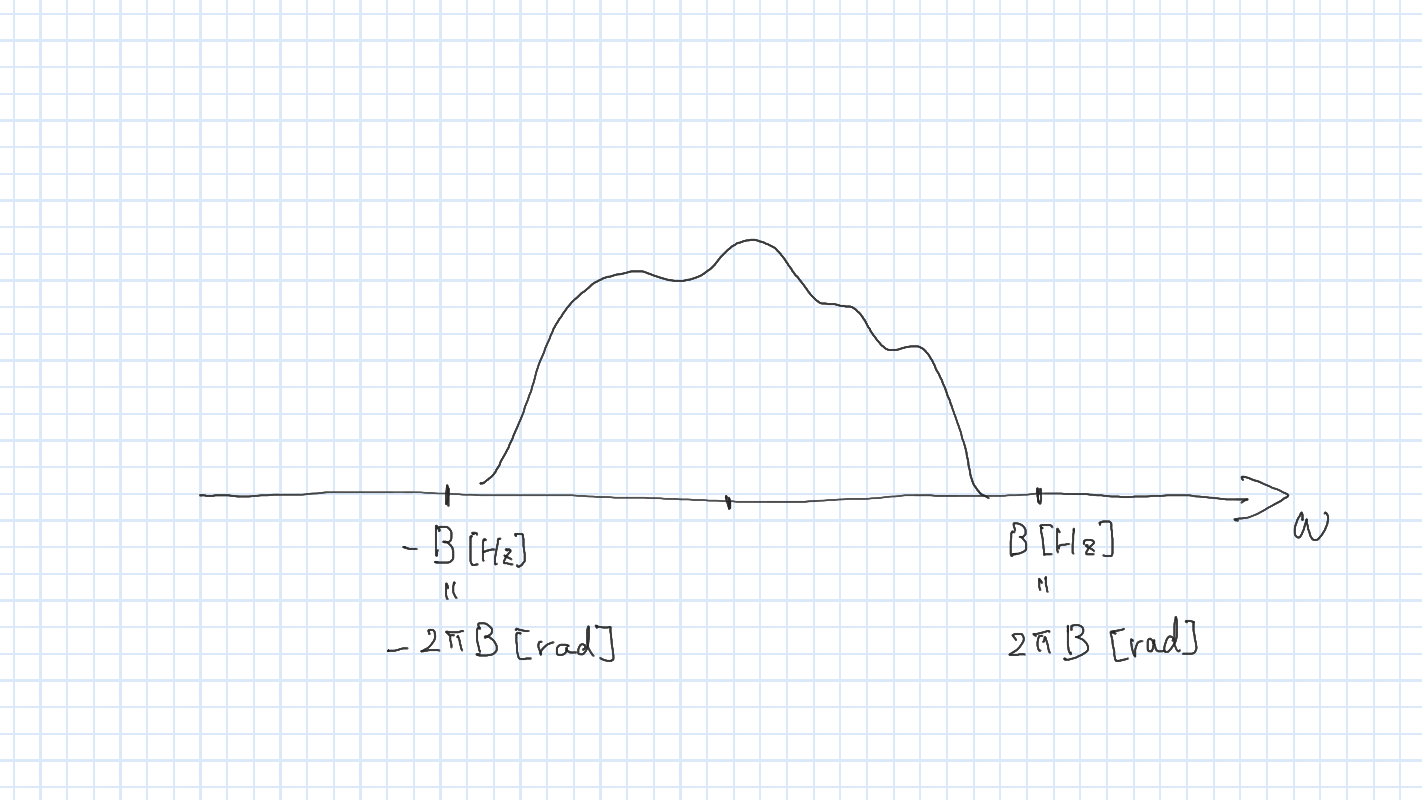
• step 1

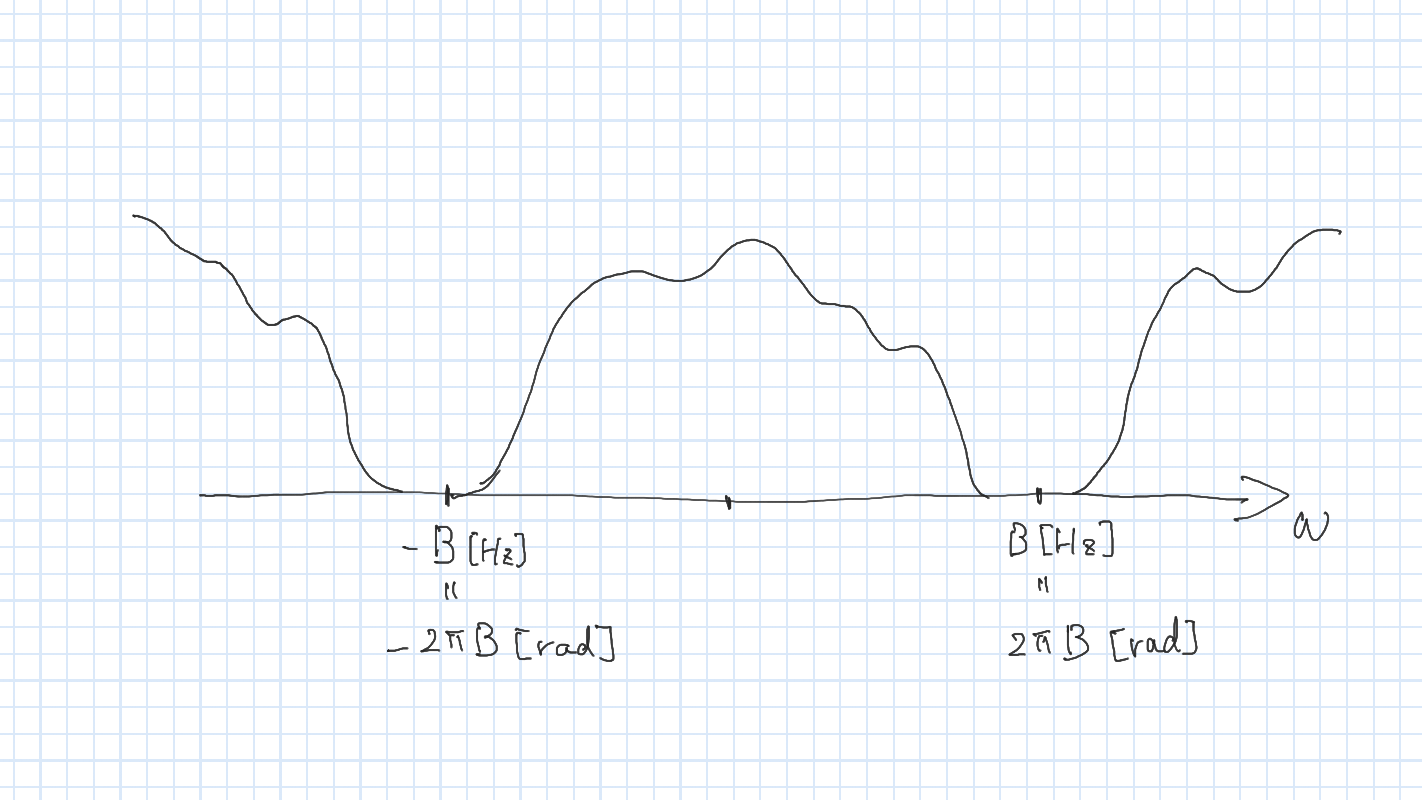
  定理の仮定より \(f(t)\) の Fourier 変換を \(\hat{f}(\omega)\) の台 (0でない \(\omega\) の領域) は \((-2\pi B, 2\pi B)\) である．

  (\(B\,[\mathrm{Hz}]=2\pi B\,[\mathrm{rad}]\))

• step 2

  \(\hat{f}\) を \(2\pi\cdot 2B\) ごとに繰り返したものを \(\tilde{f}\) とする．

  これは周期 \(2\pi\cdot 2B\) を持つ周期関数なので Fourier 級数展開が存在する．

• step 3

  周期 \(2\pi\) の Fourier 級数展開の基底を

  \begin{equation} \phi_{n}(\omega)=\frac{1}{\sqrt{2\pi}}e^{in\omega} \end{equation}

  とすると， 周期 \(2\pi\cdot 2B\) の基底は

  \begin{equation} \psi_{n}(\omega)=\phi_{n}\left(\frac{\omega}{2B}\right)\frac{1}{\sqrt{2B}} \end{equation}

  となる．

• step 4

  \(\tilde{f}\) の Fourier 級数展開は

  \begin{equation} \tilde{f}(\omega) = \sum_{n=-\infty}^{\infty} \left\langle \tilde{f}, \psi_{n} \right\rangle \psi_{n}(\omega) \end{equation}

  で与えられる．

• step 5

  \begin{align} \tilde{f}(\omega) &=\frac{1}{2\pi\cdot 2B} \sum_{n=-\infty}^{\infty} e^{i\left(\frac{n}{2B}\right)\omega} \int_{-2\pi B}^{2\pi B}\tilde{f}(\xi) e^{-i\left(\frac{n}{2B}\right)\xi}d\xi\\ &=\frac{1}{2\pi\cdot 2B} \sum_{n=-\infty}^{\infty} e^{i\left(\frac{n}{2B}\right)\omega} \int_{-2\pi B}^{2\pi B}\hat{f}(\xi) e^{-i\left(\frac{n}{2B}\right)\xi}d\xi \end{align}

  • 1周期分の積分範囲に注意して \(\tilde{f}\) をもとの \(\hat{f}\) で置き換える

• step 6

  \begin{align} \tilde{f}(\omega) &=\frac{1}{2\pi\cdot 2B} \sum_{n=-\infty}^{\infty} e^{i\left(\frac{n}{2B}\right)\omega} \int_{-2\pi B}^{2\pi B}\hat{f}(\xi) e^{-i\left(\frac{n}{2B}\right)\xi}d\xi\\ &=\frac{1}{2\pi\cdot 2B} \sum_{n=-\infty}^{\infty} e^{i\left(\frac{n}{2B}\right)\omega} \int_{-\infty}^{\infty}\hat{f}(\xi) e^{-i\left(\frac{n}{2B}\right)\xi}d\xi \end{align}

  • \(\hat{f}\) は区間 \((-2\pi B, 2\pi B)\) の外では0

• step 7

  \begin{align} \tilde{f}(\omega) &=\frac{1}{2\pi\cdot 2B} \sum_{n=-\infty}^{\infty} e^{i\left(\frac{n}{2B}\right)\omega} \int_{-\infty}^{\infty}\hat{f}(\xi) e^{-i\left(\frac{n}{2B}\right)\xi}d\xi\\ &=\frac{1}{\sqrt{2\pi}\cdot 2B} \sum_{n=-\infty}^{\infty} e^{i\left(\frac{n}{2B}\right)\omega} f\left(-\frac{n}{2B}\right) \end{align}

  • \(x=-n/2B\) における \(\hat{f}\) の Fourier 逆変換

    \begin{equation} f\left(-\frac{n}{2B}\right) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}\hat{f}(\xi) e^{i\left(-\frac{n}{2B}\right)\xi}d\xi \end{equation}

• step 8

  \begin{equation} \hat{h}_{B}(\omega) = \Xi_{(-2\pi B,2\pi B)}(\omega) = \begin{cases} 1,&|\omega|<2\pi B\\ 0,&\text{otherwise} \end{cases} \end{equation}

  とすると

  \begin{align} f(t) &=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\hat{f}(\omega) e^{i\omega t}d\omega\\ &=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\hat{h}_{B}(\omega)\tilde{f}(\omega) e^{i\omega t}d\omega \end{align}

  • \(\hat{h}_{B}\) は \(\tilde{f}\) から \(\hat{f}\) を取り出す周波数フィルタ

• step 9

  \begin{align} f(t) &=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\hat{h}_{B}(\omega) \frac{1}{\sqrt{2\pi}\cdot 2B} \sum_{n=-\infty}^{\infty} e^{i\left(\frac{n}{2B}\right)\omega} f\left(-\frac{n}{2B}\right) e^{i\omega t}d\omega\\ &=\frac{1}{2\pi\cdot 2B} \sum_{n=-\infty}^{\infty} f\left(-\frac{n}{2B}\right) \int_{-2\pi B}^{2\pi B} e^{i\left(t+\frac{n}{2B}\right)\omega}d\omega \end{align}

  • \(\hat{h}_{B}\) の定義に従って積分領域を書き換える

• step 10

  \begin{align} f(t) &=\frac{1}{2\pi\cdot 2B} \sum_{n=-\infty}^{\infty} f\left(-\frac{n}{2B}\right) \int_{-2\pi B}^{2\pi B} e^{i\left(t+\frac{n}{2B}\right)\omega}d\omega\\ &=\sum_{n=-\infty}^{\infty} \frac{\sin 2\pi B\left(t+\frac{n}{2B}\right)}{2\pi B\left(t+\frac{n}{2B}\right)} f\left(-\frac{n}{2B}\right)\\ &=\sum_{n=-\infty}^{\infty} \frac{\sin 2\pi B\left(t-\frac{n}{2B}\right)}{2\pi B\left(t-\frac{n}{2B}\right)} f\left(\frac{n}{2B}\right) \end{align}

• step 11

  以上から， \(f(t)\) は \(1/2B\) ごとのサンプル点 \(f(n/2B)\) を用いて完全に再構成できる．

定理に関する注意

• 直感的な意味

  正弦波は山と谷の値が与えられれば補間できるので， 一番高い周波数でも1周期の間に2点の標本があれば良い．

• Nyquist 周波数での挙動

  周波数 \(B\) で \(\theta\) の値によって位相と振幅が異なる 次の波形を考える．

  \begin{equation*} f(t) = \frac{\cos(2\pi Bt+\theta)}{\cos\theta} =\cos(2\pi Bt)-\sin(2\pi Bt)\tan\theta \end{equation*}

  標本点を \({n}/{2B}\) とすると

  \begin{align*} f\left(\frac{n}{2B}\right) &=(-1)^{n}-0\cdot\tan\theta =(-1)^{n} \end{align*}

  \(\theta\) によらないため， サンプリングンレート \(2B\) の標本点からは \(\theta\) の値を推定することはできない．

エイリアシング

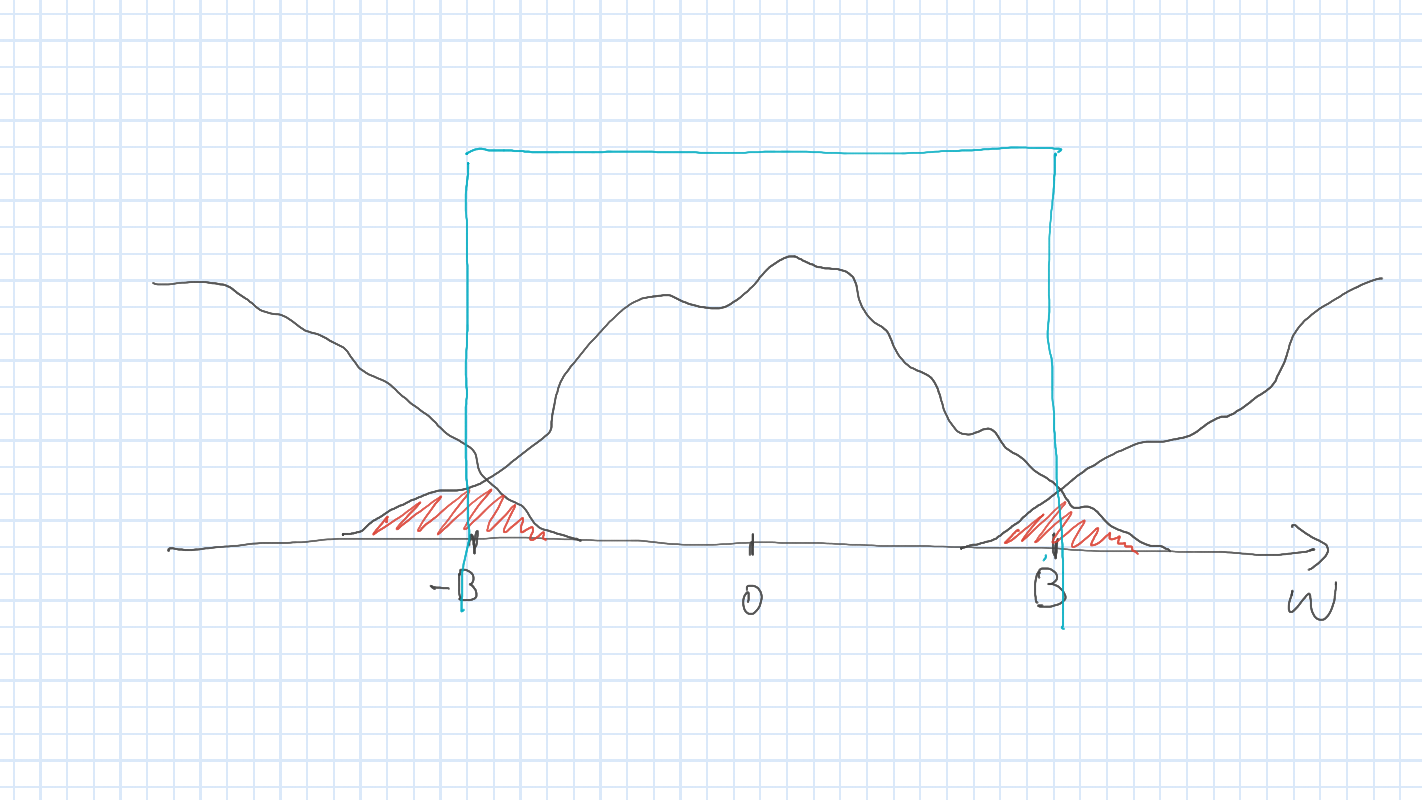
• 定理の前提

  信号の Fourier 変換が \((-2\pi B,2\pi B)\) 以外で0である．

• 成立しない場合に生じる雑音
  • エイリアシング (aliasing)
  • 折り返し雑音 (folding noise)

• 雑音の原因

  \(4\pi B\) 周期の関数 \(\tilde{f}\) を構成する際に重なりが生じ， \((-2\pi B,2\pi B)\) 領域を切り出しても 元に戻すことができない．

演習

練習問題

• サンプリング周波数

  CD (コンパクトディスク) のサンプリング周波数は 44.1 [kHz] である． CD で完全に再現される周波数はどのような範囲にあると考えられるか?

今回のまとめ

• デジタル信号処理
  • アナログとデジタル
  • 標本化と量子化
• 標本化定理
  • Nyquist 周波数
  • サンプリング周波数
  • エイリアシング