線形フィルタ回路

信号処理 - 第9講

(Press ? for help, n and p for next and previous slide)

村田 昇

前回のおさらい

フィルタ

  • 定義

    入力 \(f(t)\) を変換して出力 \(g(t)\) を生成する機構

filter1.png


線形性

  • 定義

    2つの入出力関係を考えたとき， 入力の線形結合がそのまま出力に反映される性質

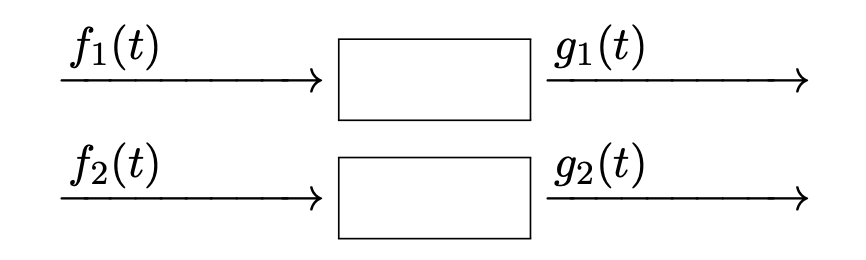
filter2.png

filter3.png


時不変性

  • 定義

    入力の時刻が \(s\) ずれた場合，出力も \(s\) だけずれる性質

    • 時間が経過してもフィルタの性質は変わらない

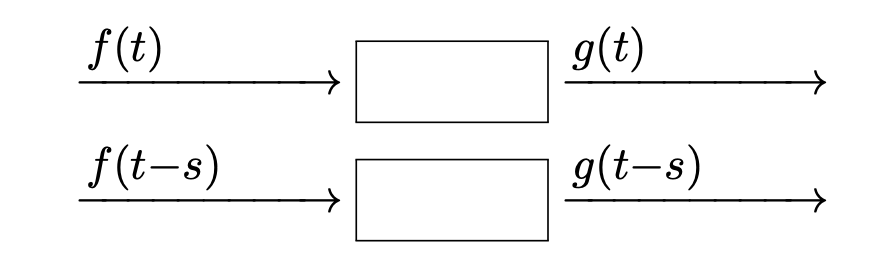
filter5.png


線形時不変フィルタの数学的表現

  • フィルタの積分表現

    \begin{equation} g(t)=\int_{-\infty}^{\infty} f(s)h(t{-}s)ds \end{equation}

  • インパルス応答

    \begin{equation} h(t) =\int_{-\infty}^{\infty}\delta(s)h(t-s)ds =\int_{-\infty}^{\infty}h(s)\delta(t-s)ds \end{equation}
    • \(h(t)\) はフィルタに \(\delta(t)\) を入力した時の出力でもある

Fourier変換による表現

  • 時間領域では畳み込み積分

    \begin{equation} g(t) =\int_{-\infty}^{\infty}h(t-s)f(s)ds = h{*}f(t) \end{equation}

    • 周波数領域では関数の積

      \begin{equation} \hat{g}(\omega) = \sqrt{2\pi}\cdot\hat{h}(\omega)\cdot\hat{f}(\omega) \end{equation}
    • フィルタの機能は周波数毎の振幅と位相の変換

因果的フィルタ

  • 定義

    \begin{equation} h(t)=0\;(t<0) \end{equation}
    • 時刻0にインパルスが入力される前には何も出力がされない

  • 因果的フィルタの畳み込み

    時刻 \(t\) での出力は 時刻 \(t\) 以前での入力のみにより定まる

    \begin{equation} g(t)=\int_{-\infty}^{t}f(s)h(t-s)ds \end{equation}

演習


練習問題

  • 以下の問に答えよ
    • 関数 \(t e^{-\frac{t^2}{2}}\) を Fourier 変換せよ
    • 関数 \(\Xi_{(-1,1)}(t)\) を Fourier 変換せよ
    • 関数 \((\sin(\omega)/\omega)^{2}\) を 逆 Fourier 変換せよ

フィルタ回路

インパルス応答とは

  • \(\delta(t)\) を入力した時のフィルタ出力

    \begin{equation} h(t) =\int_{-\infty}^{\infty}\delta(s)h(t-s)ds \end{equation}
  • 物理的には 面積1 (\(\Delta \times 1/\Delta\)) の矩形波に対する出力を 時間幅 \(\Delta\to0\) としたときの波形

2端子対回路

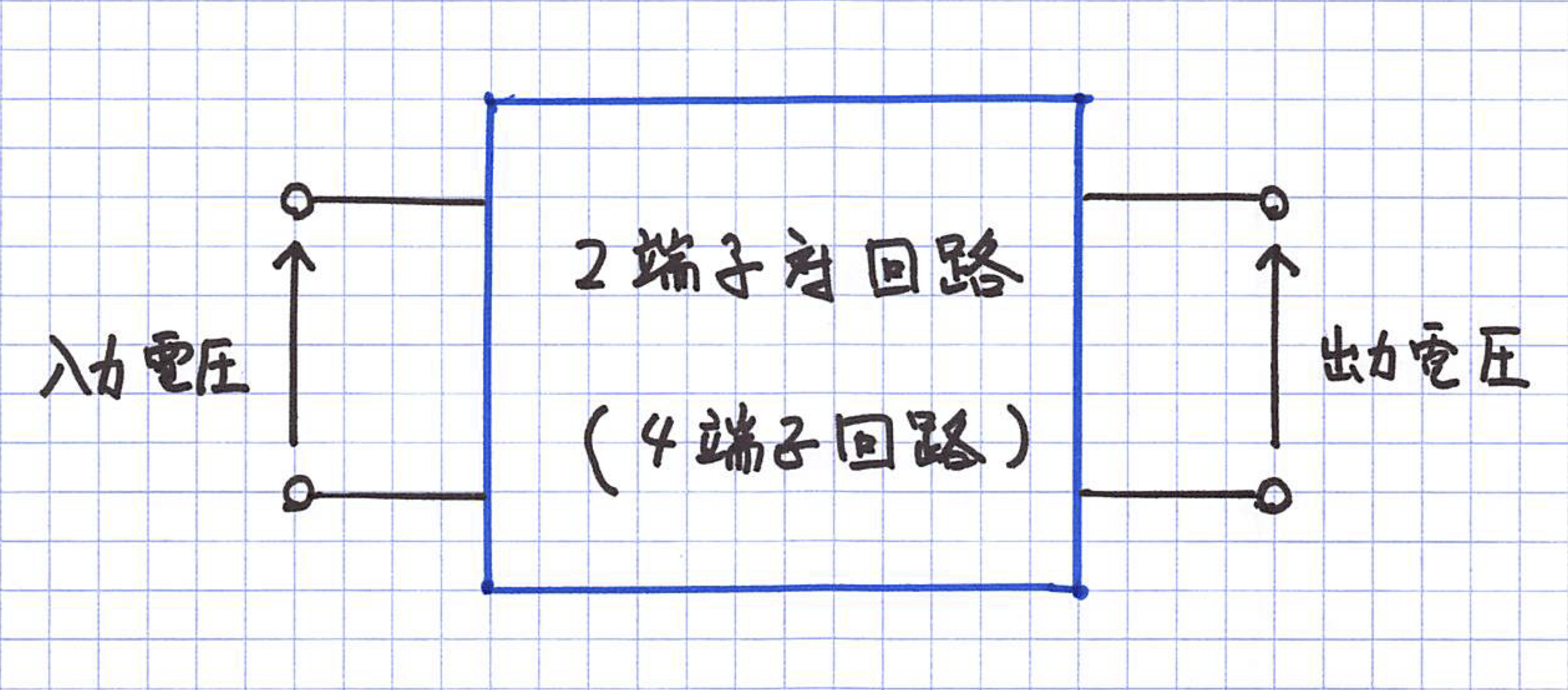
信号処理 1.png


例題

  • 以下の回路の時間領域での入出力関係を求めよ．
  • 同じく周波数領域での入出力関係を求めよ．

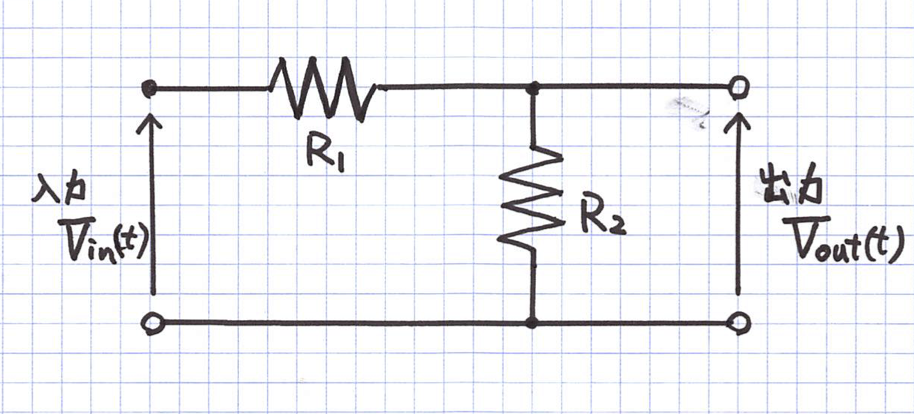
信号処理 2.png


解答

  • 時間領域

    \begin{equation} V_{out}(t) =\frac{R_{2}}{R_{1}+R_{2}}V_{in}(t) \end{equation}

  • 周波数領域

    \begin{equation} \hat{V}_{out}(\omega) =\frac{R_{2}}{R_{1}+R_{2}}\hat{V}_{in}(\omega) \end{equation}
  • 同じ形になることに注意

演習


練習問題

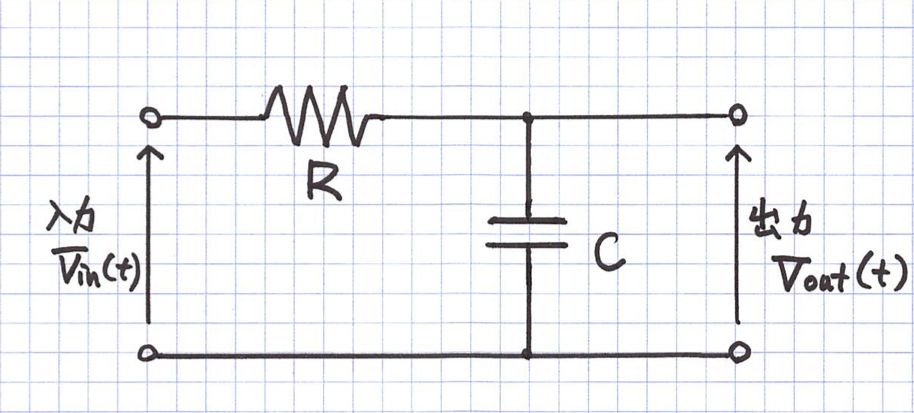
  • 以下の回路の時間領域での入出力関係を求めよ．
  • 同じく周波数領域での入出力関係を求めよ．

信号処理 3.png


逆 Fourier 変換を用いた解析

インパルス応答

  • 逆 Fourier 変換

    式を見易くするため \(a=1/CR\) とおく

    \begin{align} h(t) &=\mathcal{F}^{-1}[\hat{h}](t)\\ &=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \hat{h}(\omega)e^{i\omega t}d\omega\\ &=\frac{a}{2\pi i}\int_{-\infty}^{\infty} \frac{e^{i\omega t}}{\omega-ia}d\omega \end{align}

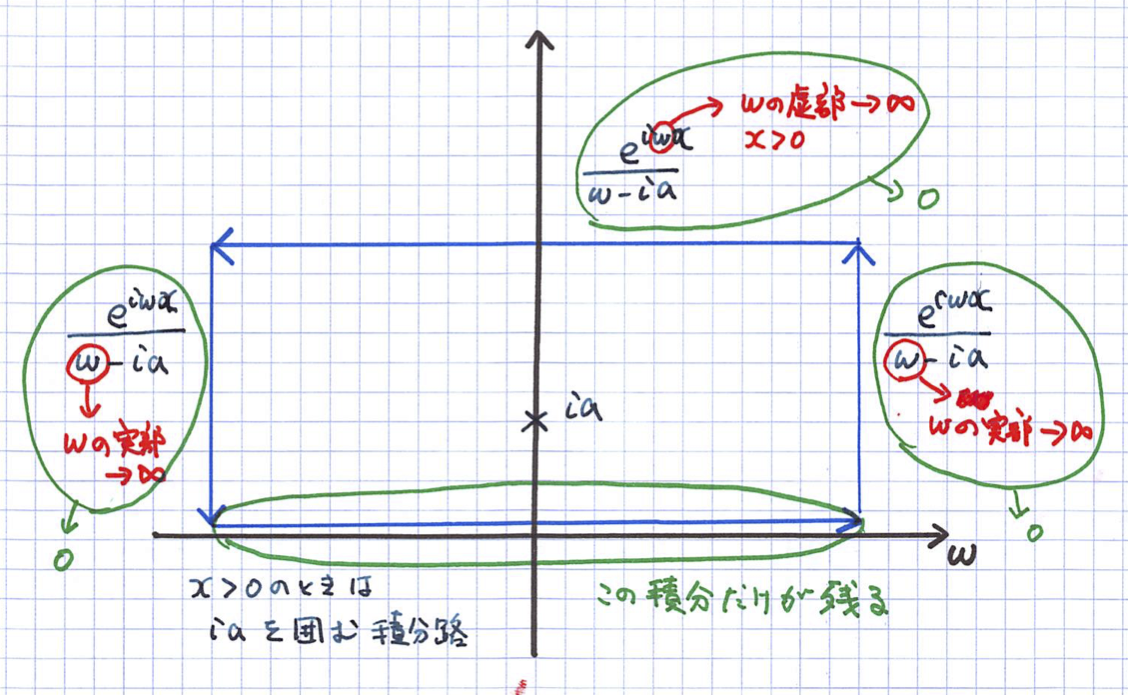
  • 複素積分の積分路
    • \(t>0\) のとき， \(ia\) を囲む上半平面
    • \(t<0\) のとき， 下半平面

信号処理 4.png


  • 留数定理

    積分路が孤立特異点 \(c\) を含むとき以下が成り立つ

    \begin{equation} \frac{1}{2\pi i}\oint f(z)dz =\mathrm{Res}_{z=c}f(z) =\lim_{z\to c}(z-c)f(z) \end{equation}

  • 計算結果

    \begin{equation} h(t) = \begin{cases} a e^{-at}=\frac{1}{CR}e^{-\frac{t}{CR}},&t>0\\ 0,&t<0 \end{cases} \end{equation}

演習


練習問題

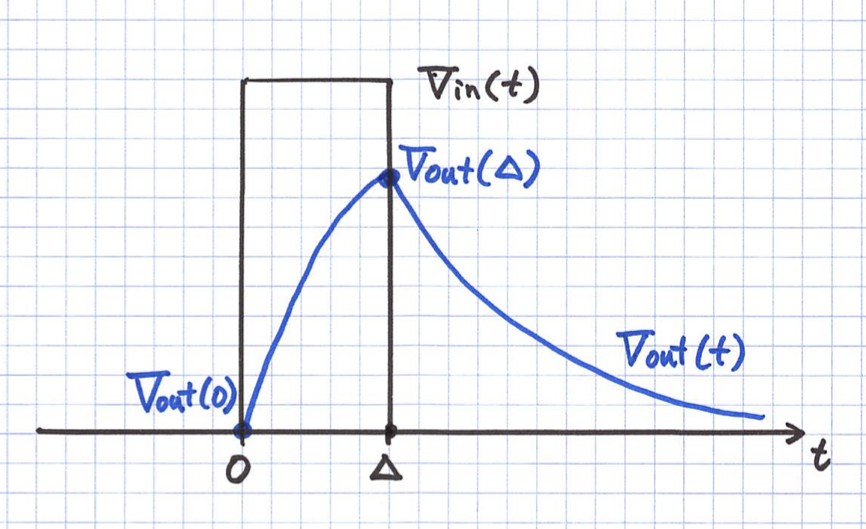
  • 矩形波の入力に対して微分方程式を直接解き， その極限からインパルス応答を求めよ．

信号処理 5.png


今回のまとめ

  • 線形フィルタ回路
    • 時間領域での表現(微分方程式)
    • 周波数領域での表現(関数の積)
    • フィルタの周波数特性
    • インパルス応答の求め方