主成分分析 - 考え方
数理科学続論J
(Press ? for help, n and p for next and previous slide)
村田 昇
2019.11.08
講義の予定
- 第1日: 主成分分析の考え方
- 第2日: 分析の評価と視覚化
主成分分析の考え方
主成分分析 (principal component analysis)
- 多数の変量のもつ情報の分析・視覚化
- 変量を効率的に縮約して少数の特徴量を構成する
- 変量の間の関係を明らかにする
記号の準備
- 変数: \(X_1,\dotsc,X_p\)
- 特徴量: \(Z_1,\dotsc,Z_d\) ( \(d\leq p\) )
変数と特徴量の関係 (線形結合):
\begin{equation} Z_k=a_{1k}X_1+\cdots+a_{pk}X_p\quad(k=1,\dotsc,d) \end{equation}特徴量は定数倍の任意性があるので以下を仮定:
\begin{equation} \|\boldsymbol{a}_k\|^2:=\sum_{j=1}^pa_{jk}^2=1 \end{equation}
主成分分析の用語
- 特徴量 \(Z_k\): 第 \(k\) 主成分(得点)
(principal component score) - 係数ベクトル \(\boldsymbol{a}_k\):
第 \(k\) 主成分方向
(principal component direction)
または第 \(k\) 主成分負荷量
(principal component loading)
主成分分析の目的
- 目的: 主成分得点 \(Z_1,\dots,Z_d\) が変数 \(X_1,\dotsc,X_p\) の情報を 効率よく反映するように 主成分方向 \(\boldsymbol{a}_1,\dotsc,\boldsymbol{a}_d\) を 観測データから うまく 決定する
- 分析の方針: (以下は同値)
- データの情報を最大限保持する変量の線形結合を構成
- データの情報を最大限反映する座標(方向)を探索
- 教師なし学習 の代表的手法の1つ
- 次元縮約: 入力をできるだけ少ない変数で表現
- 特徴抽出: 情報処理に重要な特性を変数に凝集
R: 主成分分析を実行する関数
- Rの標準的な関数:
prcomp()およびprincomp() - 計算法に若干の違いがある
- 数値計算の観点からみると
prcomp()が優位 princomp()はS言語(商用)との互換性を重視した実装
- 数値計算の観点からみると
- 本講義では
prcomp()を利用
R: 関数 prcomp() の使い方
- 基本的にデータフレームを用いる:
- データフレーム
mydata: 必要な変数を含むデータフレーム - 列名: x1の変数名, …, xpの変数名
- データフレーム
## データフレームを全て用いる場合 prcomp(mydata) ## 列名を指定する(formulaを用いる)場合 prcomp( ~ x1の変数名 + ... + xpの変数名, data = mydata)
演習: 2次元人工データの主成分分析
- 07-toy.r の前半を確認してみよう
第1主成分の計算
記号の準備
- \(\{(x_{i1},\dots,x_{ip})\}_{i=1}^n\): \(n\) 個の \(p\) 次元観測データ
- \(\boldsymbol{x}_i=(x_{i1},\dots,x_{ip})^\top\): \(i\) 番目の観測データ
(\(p\) 次元空間内の1点) - \(\boldsymbol{a}=(a_1,\dots,a_p)^\top\): 長さ1の \(p\) 次元ベクトル
- \(\boldsymbol{a}\cdot\boldsymbol{x}_i\): データ \(\boldsymbol{x}_i\) の \(\boldsymbol{a}\) 方向成分の長さ(スカラー)
- \((\boldsymbol{a}\cdot\boldsymbol{x}_i)\,\boldsymbol{a}\):
(スカラー \(\times\) ベクトル)
方向ベクトル \(\boldsymbol{a}\) をもつ直線上への点 \(\boldsymbol{x}_i\) の直交射影
幾何学的描像
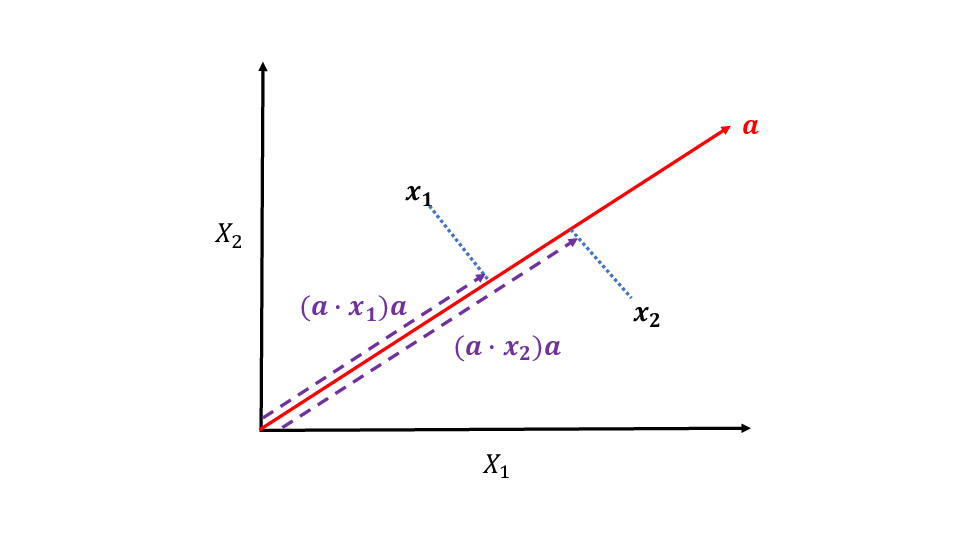
Figure 1: 観測データの直交射影 (\(p=2,n=2\) の場合)
ベクトル \(\boldsymbol{a}\) の選択の指針
- ベクトル \(\boldsymbol{a}\) を うまく 選んで 観測データ \(\boldsymbol{x}_1,\dots,\boldsymbol{x}_n\) の情報を最大限保持する 1変量データ \(\boldsymbol{a}\cdot\boldsymbol{x}_1,\dotsc,\boldsymbol{a}\cdot\boldsymbol{x}_n\) を構成する
観測データ \(\boldsymbol{x}_1,\dotsc,\boldsymbol{x}_n\) のばらつきを最も反映する方向を最適なベクトル \(\boldsymbol{a}\) とする
\begin{equation} \arg\max_{\boldsymbol{a}} \sum_{i=1}^n(\boldsymbol{a}\cdot\boldsymbol{x}_i -\boldsymbol{a}\cdot\bar{\boldsymbol{x}})^2, \quad \bar{\boldsymbol{x}} = \frac{1}{n}\sum_{i=1}^n\boldsymbol{x}_i, \end{equation}
ベクトル \(\boldsymbol{a}\) の最適化問題
制約条件 \(\|\boldsymbol{a}\|=1\) の下で関数
\begin{equation} f(\boldsymbol{a}) = \sum_{i=1}^n(\boldsymbol{a}\cdot\boldsymbol{x}_i -\boldsymbol{a}\cdot\bar{\boldsymbol{x}})^2 \end{equation}を最大化せよ
- この最大化問題は必ず解をもつ:
- \(f(\boldsymbol{a})\) は連続関数
- 集合 \(\{\boldsymbol{a}\in\mathbb{R}^p:\|\boldsymbol{a}\|=1\}\) はコンパクト(有界閉集合)
ベクトル \(\boldsymbol{a}\) の性質
\(f(\boldsymbol{a})\) の極大値を与える \(\boldsymbol{a}\) は 以下で定義される行列 \(\boldsymbol{X}^\top\boldsymbol{X}\) の 固有ベクトル:
\begin{equation} \boldsymbol{X} = \begin{pmatrix} \boldsymbol{x}_{1}^\top-\bar{\boldsymbol{x}}^\top \\ \vdots \\ \boldsymbol{x}_{n}^\top-\bar{\boldsymbol{x}}^\top \end{pmatrix} = \begin{pmatrix} x_{11}-\bar{x}_1 & \cdots & x_{1p}-\bar{x}_p\\ \vdots & & \vdots \\ x_{n1}-\bar{x}_1 & \cdots & x_{np}-\bar{x}_p \end{pmatrix} \end{equation}(回帰分析のデザイン行列,Gram 行列を参照)
- 関数値 \(f(\boldsymbol{a})\) はこの固有ベクトルに対する固有値
第1主成分
- 求める \(\boldsymbol{a}\) は 行列 \(\boldsymbol{X}^\top\boldsymbol{X}\) の最大固有ベクトル (長さ1)
- \(f(\boldsymbol{a})\) は 行列 \(\boldsymbol{X}^\top\boldsymbol{X}\) の最大固有値
- 第1主成分方向: ベクトル \(\boldsymbol{a}\)
第1主成分得点:
\begin{equation} z_{i1}=a_1x_{i1}+\cdots+a_px_{ip}\quad(i=1,\dots,n) \end{equation}
演習: 第1主成分の計算
- 07-eigen.r を確認してみよう
第2主成分以降の計算
Gram行列の性質
- \(\boldsymbol{X}^\top\boldsymbol{X}\) は非負定値対称行列
- \(\boldsymbol{X}^\top\boldsymbol{X}\) の固有値は0以上の実数
固有値を重複を許して降順に並べる
\begin{equation} \lambda_1\geq\dotsb\geq\lambda_p\quad(\geq0) \end{equation}固有値 \(\lambda_j\) に対する固有ベクトルを \(\boldsymbol{a}_j\)(長さ1)とする
\begin{equation} \|\boldsymbol{a}_j\|=1\quad (j=1,\dotsc,p) \end{equation}
\(\boldsymbol{a}_1,\dotsc,\boldsymbol{a}_p\) は 互いに直交 するようとることができる
\begin{equation} j\neq k \quad\Rightarrow\quad \boldsymbol{a}_j\cdot\boldsymbol{a}_k=0 \end{equation}
第2主成分の考え方
- 第1主成分:
- 主成分方向: ベクトル \(\boldsymbol{a}_1\)
- 主成分得点: \(\boldsymbol{a}_1\cdot\boldsymbol{x}_i\) (\(i=1,\dotsc,n\))
第1主成分方向に関してデータが有する情報:
\begin{equation} (\boldsymbol{a}_1\cdot\boldsymbol{x}_i)\,\boldsymbol{a}_1 \quad(i=1,\dotsc,n) \end{equation}第1主成分方向の成分を取り除いた観測データ:
\begin{equation} \tilde{\boldsymbol{x}}_i := \boldsymbol{x}_i -(\boldsymbol{a}_1\cdot\boldsymbol{x}_i)\,\boldsymbol{a}_1 \quad(i=1,\dotsc,n) \end{equation}- これに対してばらつきを最も反映する方向を求める
第2主成分の最適化問題
制約条件 \(\|\boldsymbol{a}\|=1\) の下で関数
\begin{equation} \tilde{f}(\boldsymbol{a}) = \sum_{i=1}^n(\boldsymbol{a}\cdot\tilde{\boldsymbol{x}}_i -\boldsymbol{a}\cdot\bar{\tilde{\boldsymbol{x}}})^2 \quad\text{ただし}\quad \bar{\tilde{\boldsymbol{x}}} = \frac{1}{n}\sum_{i=1}^n\tilde{\boldsymbol{x}}_i \end{equation}を最大化せよ
- 解は第2固有値 \(\lambda_2\) に対応する固有ベクトル \(\boldsymbol{a}_2\)
- 以下同様に 第 \(k\) 主成分方向は \(\boldsymbol{X}^\top\boldsymbol{X}\) の第 \(k\) 固有値 \(\lambda_k\) に対応する固有ベクトル \(\boldsymbol{a}_k\)
演習: 実データによる主成分分析
- 07-pca.r を確認してみよう
演習
- 以下のデータを用いて主成分分析を行ってみよう
- datasets::USArrests
- MASS::Cars93
- MASS::UScereal