確率密度

確率・統計 - 第3講

(Press ? for help, n and p for next and previous slide)

村田 昇

前回のおさらい

  • 一般の確率空間
    • 有限集合と無限集合
    • 集合の濃度 (無限集合は更に分類される)
      • 可算集合: 自然数，整数，有理数
      • 連続集合: 無理数，実数
    • 一般の確率測度と \(\sigma\)-加法性の関係
    • Lebesgue 測度と Borel 集合族 (応用上重要な概念)
    • “ほとんど確実に成り立つ”

確率測度と確率密度


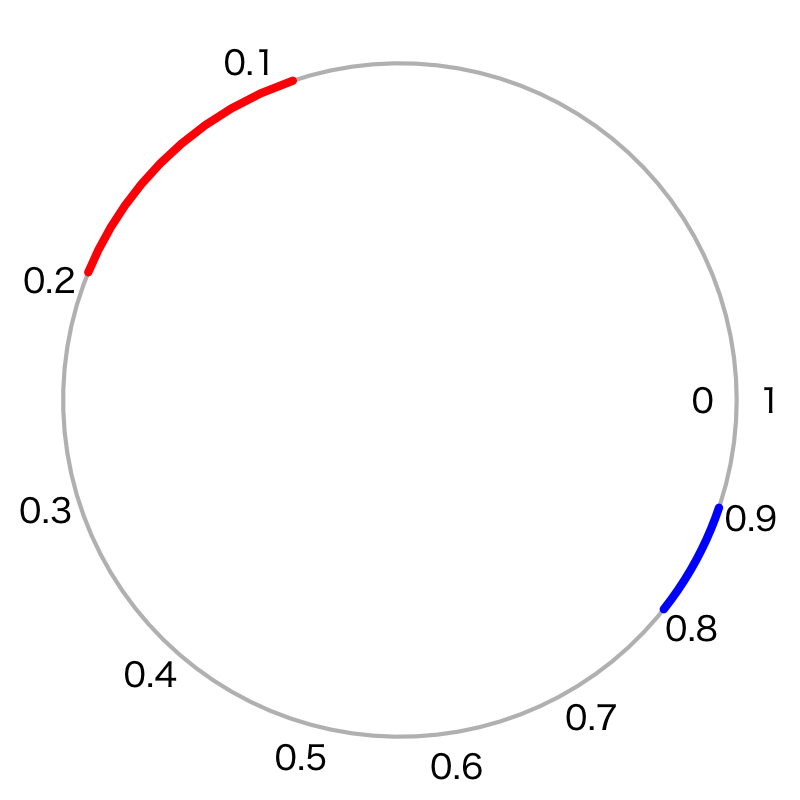
歪んだ目盛りのルーレットの例

  • 問題

    起点 \(0\) から周に沿った長さ \(l\) の位置の目盛りの値を

    \begin{equation} x=l^{2} \end{equation}

    として周長1のルーレットを作る．

    事象として同じ長さの区間 \([0.1,0.2]\), \([0.8,0.9]\) を考えたとき， その確率

    \begin{equation} P([0.1,0.2]),\quad P([0.8,0.9]) \end{equation}

    の大小関係はどのような関係になるか?


  • 解答

    \begin{equation} P([0.1,0.2]) > P([0.8,0.9]) \end{equation}

roulette.png


  • 考え方

    これまで扱ってきた単純なルーレットに対応づけて考えればよい．

    • 歪んだ目盛りの指す区間: \([a,b]\)
    • これまでのルーレットでの区間: \([\sqrt{a},\sqrt{b}]\)

    したがって確率測度は以下で計算される．

    \begin{equation} P([a,b]) = \sqrt{b}-\sqrt{a} \end{equation}

一様でない抜き出しの例

  • 問題

    “\(\Omega=[0,1]\) の点を異なる確率で抜き出す” という試行において， 区間 \([0,0.5)\) から点が抜き出される事象と， 区間 \([0.5,1]\) から点が抜き出される事象を比較すると， 前者より後者が3倍起こりやすい状況を考える．

    このとき確率測度をどのように定義すれば良いか?


  • 解答

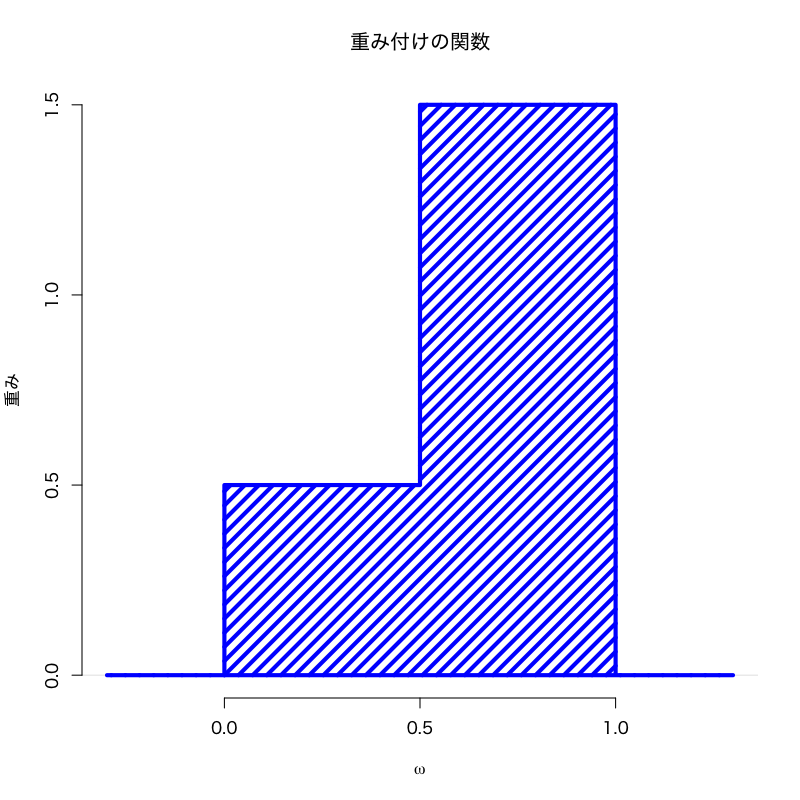
density.png

\begin{equation} f(x)= \begin{cases} 0.5, & (0\le x< 0.5)\\ 1.5, & (0.5\le x\le 1) \end{cases} \end{equation}

として， 確率測度を

\begin{equation} P(A)=\int_{A}f(\omega)d\omega \end{equation}

で定義する．


  • 確率の偏りの確認

    例えば区間 \([0.1,0.2]\) と \([0.8,0.9]\) を比べてみる

    \begin{align} P([0.1,0.2])&=\int_{0.1}^{0.2}f(\omega)d\omega =\left[0.5\omega\right]_{0.1}^{0.2}=0.05\\ P([0.8,0.9])&=\int_{0.8}^{0.9}f(\omega)d\omega =\left[1.5\omega\right]_{0.8}^{0.9}=0.15 \end{align}

確率測度の条件 (再掲)

  • 以下の3つの条件が成立する

    \begin{align} (P.1)\quad &P(A)\ge 0,\; A\in\mathcal{F}\\ (P.2)\quad &P\biggl(\sum_{n=1}^\infty A_n\biggr) =\sum_{n=1}^\infty P(A_n),\; A_n\in\mathcal{F}\\ (P.3)\quad &P(\Omega)=1 \end{align}

積分による表現の正当性

  • (P.1) \(f(x)\) の正値性から明らか
  • (P.2) 積分区間を分割しても積分値が変わらないという積分の性質から明らか

  • (P.3) 区間 \([0,1]\) 上の積分

    \begin{equation} P([0,1])=\int_{0}^{1}f(\omega)d\omega =0.5\times0.5+0.5\times1.5=1 \end{equation}

    より全確率が \(1\) となっている


確率密度

  • 定義

    確率測度がある関数の積分

    \begin{equation} P(A)=\int_{A}f(\omega)d\omega \end{equation}

    で書かれているとき， その被積分関数を 確率密度(関数) (probability density function) という．

    また確率密度を持つ確率測度を 絶対連続 (absolutely continuous) な分布と呼ぶ．

    • 標本空間上で積分が定義できる場合であることに注意

確率密度の例

  • 歪んだ目盛りのルーレット

    歪んだ目盛をもつルーレットの確率密度は， 任意の \(a,b\;(0 < a < b\le1)\) に対して

    \begin{equation} P([a,b]) = \int_{a}^{b}f(\omega)d\omega = \sqrt{b}-\sqrt{a} \end{equation}

    となる 以下の関数 \(f\) である．

    \begin{equation} f(\omega)= \begin{cases} \frac{1}{2\sqrt{\omega}},&(0<\omega\le1)\\ 0,&(\text{それ以外}) \end{cases} \end{equation}

演習


練習問題

  • 起点 \(0\) から周に沿った長さ \(l\) の位置に対して， 以下のような歪んだ目盛り \(x\) を付けた 周長1のルーレットの確率密度を求めよ．
    1. \(x=\sqrt{l}\)
    2. \(x=-\log(l)\)
    3. \(x=\sin^{-1}(l)\;(0 < x\le\pi/2)\)

異なる2つの積分

積分の考え方

  • Riemann 積分 (区分求積法に基づく)
  • Lebesgue 積分 (確率測度に基づく)

Riemann 積分

  • 定義

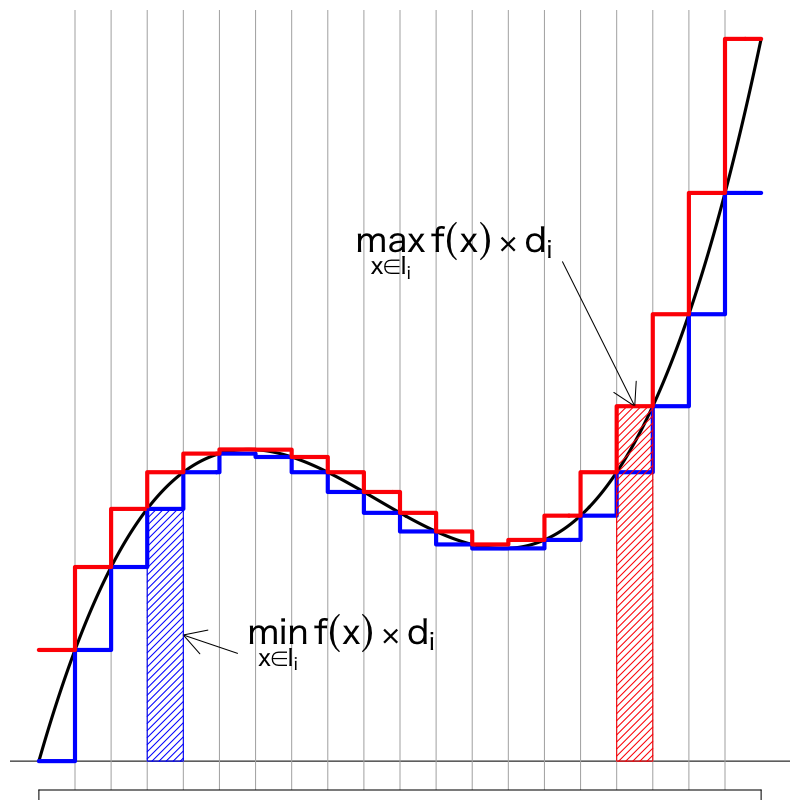
riemann.png

有界な積分領域 \(K\) を \(n\) 個の区間 \(I_i\) (幅は \(d_i\)) に分割する． 各区間における関数 \(f(x)\) の最小値と最大値を用いて 有限和 \(s_n\),\(S_n\) を次のように定義する．

\begin{align} s_n &=\sum_{i=1}^n\min_{x\in I_i}f(x)\times d_i\\ S_n &=\sum_{i=1}^n\max_{x\in I_i}f(x)\times d_i \end{align}

  • 定義(つづき)

    各区間の大小関係から

    \begin{equation} s_n\le S_n \end{equation}

    が成り立っているが，分割を細かくしたとき， それぞれの極限が存在して， なおかつ一致するならば， これを \(f(x)\) の Riemann 積分 (Riemann integral) という．

    \begin{equation} \lim_{n\to\infty}s_n =\lim_{n\to\infty}S_n =\int_K f(x)dx \end{equation}

Lebesgue 積分

  • 定義

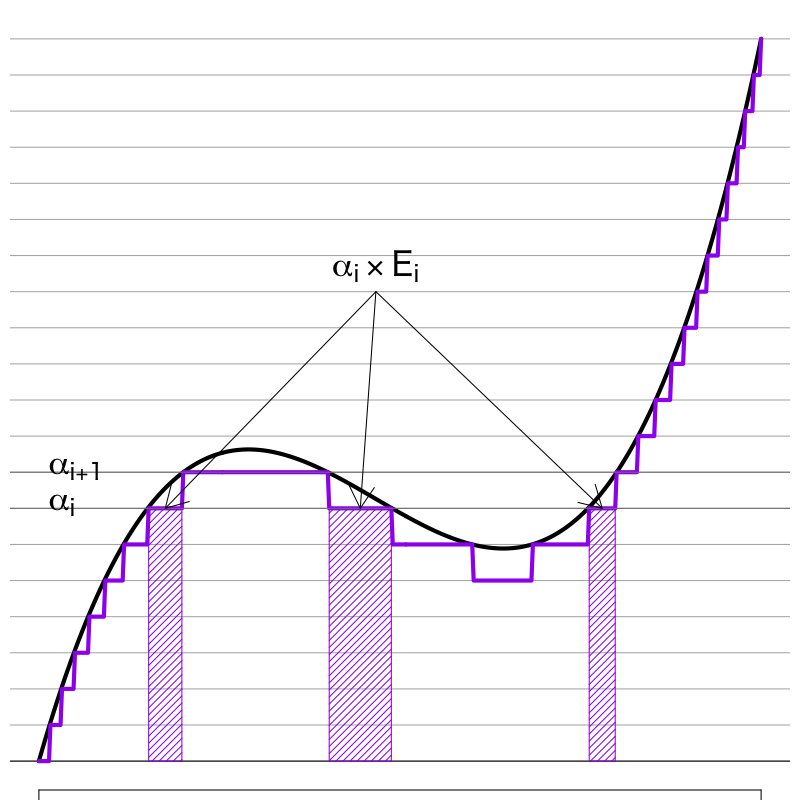
lebesgue.png

区間 \(K\) 上で定義された 関数 \(f(x)\) の値域を \(n\) 個の区間に分割する． 区間の端点を \(\alpha_i\) とし， \(f(x)\) が区間 \([\alpha_i,\alpha_{i+1})\) で値を取る \(x\) の領域を \(E_i\subset K\) で表し， \(E_i\) 上で値が \(\alpha_i\) となる 階段関数 \(f_n(x)\) (単関数)を考える．


  • 定義(つづき)

    このとき \(\mu\) を Lebesgue 測度とし， 単関数 \(f_n(x)\) の Lebesgue 積分 を

    \begin{equation} \int_K f_n(x)dx =\sum_{i=1}^n\alpha_i\mu(E_i) \end{equation}

    で定義する． 分割を細かくしたとき \(f_n(x)\) は \(f(x)\) に近づいていくが， この極限が存在するならば， これを \(f(x)\) の Lebesgue 積分 (Lebesgue integral) という．

    \begin{equation} \lim_{n\to\infty}\int_K f_n(x)dx =\int_K f(x)dx \end{equation}

表記に関する注意

  • Lebesgue 積分特有の記法

    2つの積分を明示的に区別するために， Lebesgue 積分を

    \begin{equation} \int_K f(x)\mu(dx), \quad\text{(\(\mu\)は Lebesgue 測度)} \end{equation}

    と書くことがある．

    • この講義での以降の積分は， 特に断わらないかぎり Lebesgue 積分を考える

2つの積分の違い

  • 特異な例

    \([0,1]\) 上で次のような関数

    \begin{equation} f(x)= \begin{cases} 1, & \text{\(x\)が有理数}\\ 0, & \text{\(x\)が無理数} \end{cases} \label{eq:dirichlet_fn} \end{equation}

    を考える．

    • この関数は Dirichlet の関数と呼ばれ

      \begin{equation} f(x)= \lim_{n\to\infty}\lim_{k\to\infty}\cos^{2k}(n!\pi x) \end{equation}

      と書けることが知られている


  • Riemann 積分の場合

    どんな短い区間 \(I_i\) にも有理数と無理数は混在するので

    \begin{equation} \min_{x\in I_i}f(x)=0,\quad \max_{x\in I_i}f(x)=1 \end{equation}
    \begin{align} s_n&=\sum_{i=0}^{n}0\times d_{i}=0\\ S_n&=\sum_{i=0}^{n}1\times d_{i}=1 \end{align}

    であり， \(n\) をいくら大きくしても極限は一致しない． したがってこの関数の Riemann 積分は存在しない．


  • Lebesgue 積分の場合

    適当な値域の分割において

    \begin{equation} \alpha_{i}\le 0<\alpha_{i+1},\quad \alpha_{j}\le 1<\alpha_{j+1} \end{equation}

    となるのであれば，Lebesgue 測度の性質より

    \begin{equation} \int f_{n}(x)dx = \alpha_{i}\times\mu(\text{無理数})+\alpha_{j}\times\mu(\text{有理数}) % = \alpha_{i}\cdot1+\alpha_{j}\cdot0 =\alpha_{i} \end{equation}

    となるが， \(n\to\infty\) のとき \(\alpha_{i}\to0,\;\alpha_{j}\to1\) となるので

    \begin{equation} \int f(x)dx = 0\times\mu(\text{無理数})+1\times\mu(\text{有理数}) = 0 \end{equation}

    となり Lebesgue 積分可能である．


積分の一致する条件

  • 定理

    有界閉区間 \(K\) で \(f\) が連続なら， \(K\) 上の \(f\) の Lebesgue 積分の値は Riemann 積分の値と一致する．

    • 応用上重要な問題に現れる 「あまり特殊でない関数」では ほとんど一致すると考えてよい

演習


練習問題

  • 以下の関数が \(\mathbb{R}\) 上の確率密度関数となるように \(a\) の値を定めよ．
    1. \begin{equation} f(x)= \begin{cases} 0& (x < 0)\\ \exp(ax) & (x\geq0) \end{cases} \end{equation}
    2. \begin{equation} g(x)= \begin{cases} 0& (|x|>1)\\ a \cos(\pi x/2) & (|x|\leq1) \end{cases} \end{equation}

確率密度関数の例

正規分布 (normal/Gaussian distribution)

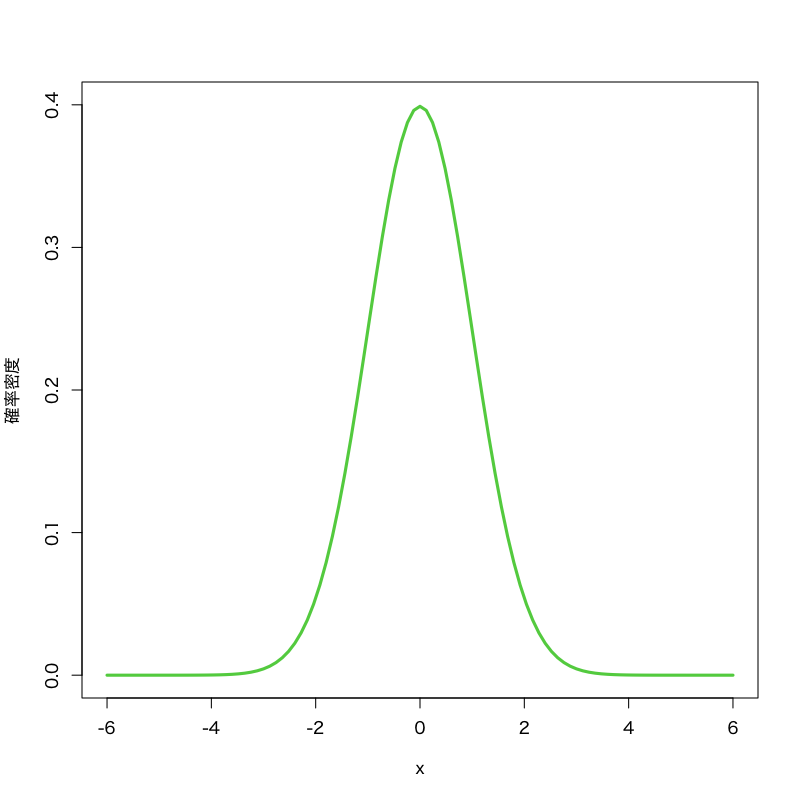
pdf_norm.png

Figure 1: 正規分布 (平均\(0\),分散\(1\))

  • 標本空間: \((-\infty,\infty)\)
  • 母数: 平均 \(\mu\), 分散 \(\sigma^{2}\)

  • 密度関数:

    \begin{equation} f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} \end{equation}
  • 備考: \(\mu=0,\sigma=1\) のとき 標準正規分布 と呼ぶ．

一様分布 (uniform distribution)

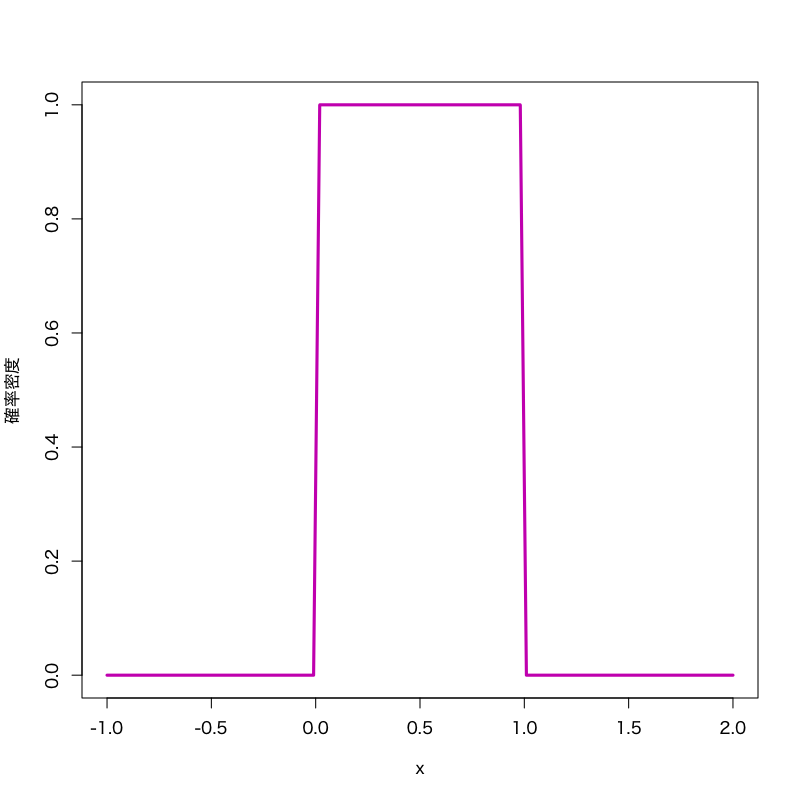
pdf_unif.png

Figure 2: 一様分布 (区間\([0,1]\))

  • 標本空間: 区間 \([a,b]\)
  • 母数: 区間の端点 \(a,b\)

  • 密度関数:

    \begin{equation} \frac{1}{b-a} \quad(b\le x\le a) \end{equation}
  • 備考: ルーレット回しの 確率密度関数に相当する．

Cauchy分布 (Cauchy distribution)

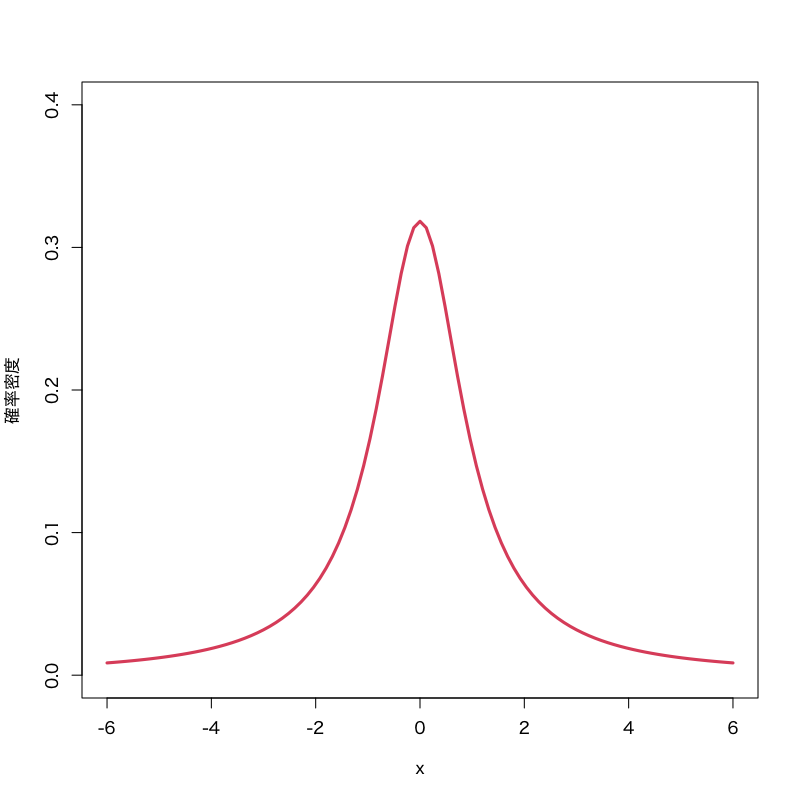
pdf_cauchy.png

Figure 3: Cauchy分布 (位置\(0\),尺度\(1\))

  • 標本空間: \((-\infty,\infty)\)
  • 母数: 位置 (location) \(\mu\) ， 尺度 (scale) \(\sigma\)

  • 密度関数:

    \begin{equation} f(x)= \frac{1}{\pi\sigma}\left(1+\frac{(x-\mu)^{2}}{\sigma^{2}}\right)^{-1} \end{equation}
  • 備考: 裾の重い分布の典型として用いられる． 正規分布の比から導かれる．

\(\chi^{2}\)-分布 (\(\chi^{2}\)-distribution)

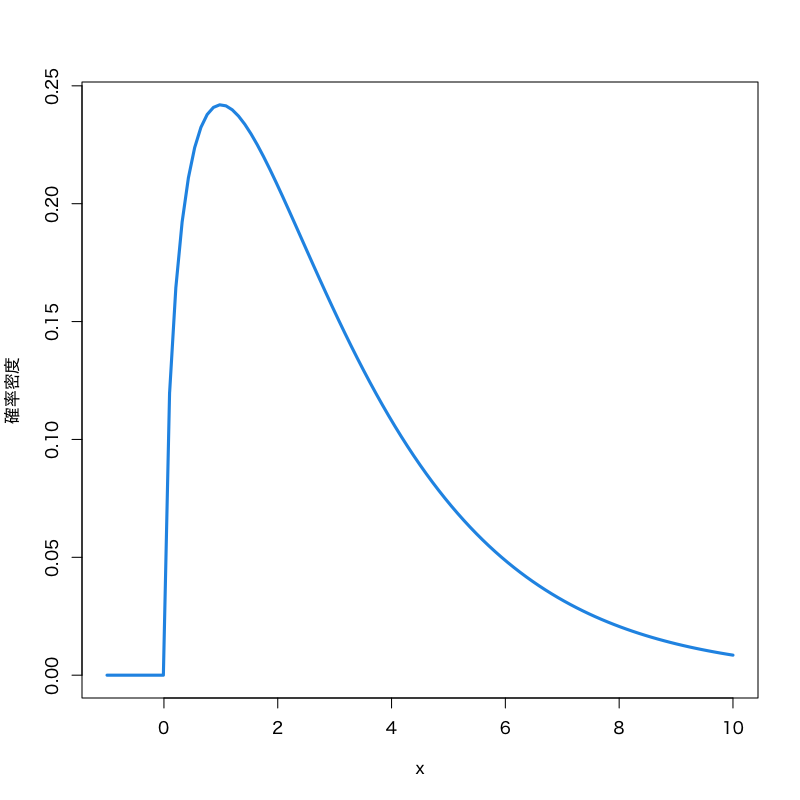
pdf_chisq.png

Figure 4: \(\chi^{2}\)-分布 (自由度\(3\))

  • 標本空間: \([0,\infty)\)
  • 母数: 自由度 \(\nu\)

  • 密度関数:

    \begin{multline} f(x)= \frac{1}{2^{\nu/2}\Gamma(\frac{\nu}{2})}x^{\nu/2-1}e^{-x/2}\\ \Gamma(z)=\int_0^\infty e^{-t}t^{z-1}dt \end{multline}
  • 備考: \(\nu\) 個の標準正規分布の2乗和の分布で， 検定に利用される．

\(t\)-分布 (Student’s \(t\)-distribution)

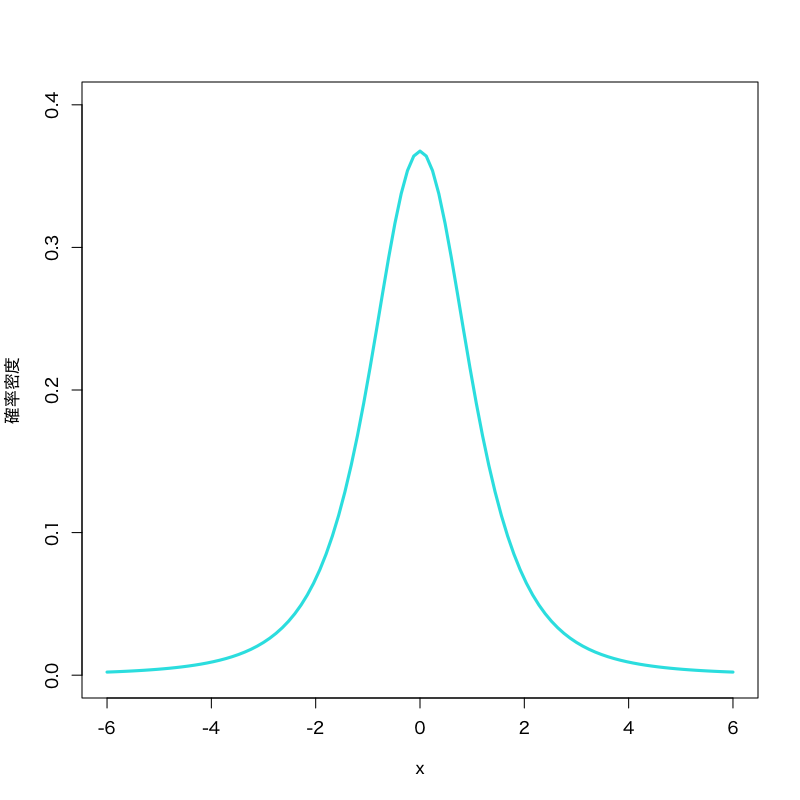
pdf_t.png

Figure 5: \(t\)-分布 (自由度\(3\))

  • 標本空間: \((-\infty,\infty)\)
  • 母数: 自由度 \(\nu\)

  • 密度関数:

    \begin{equation} f(x)= \frac{\Gamma\left(\frac{\nu+1}{2}\right)} {\sqrt{\nu\pi}\Gamma\left(\frac{\nu}{2}\right)} \left(1+\frac{x^{2}}{\nu}\right)^{-\frac{1}{2}(\nu+1)} \end{equation}
  • 備考: 標準正規分布と 自由度 \(\nu\) の \(\chi^{2}\)-分布の比の分布で， 検定に利用される．

指数分布 (exponential distribution)

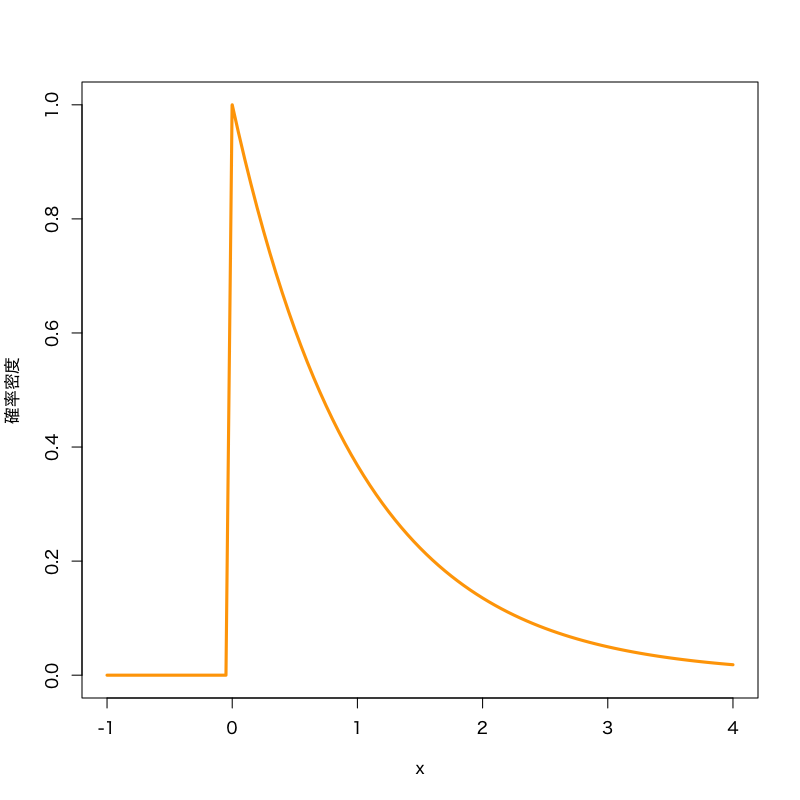
pdf_exp.png

Figure 6: 指数分布(比率\(1\))

  • 標本空間: \([0,\infty)\)
  • 母数: 比率 (rate) \(\lambda>0\)

  • 密度関数:

    \begin{equation} f(x)= \frac{1}{\lambda}e^{-\frac{x}{\lambda}} \end{equation}
  • 備考: タクシーなどの待ち時間のモデル として利用される．

確率密度がない分布

確率密度が定義されない例 (その1)

  • \(\delta\) 分布

    確率測度を

    \begin{equation} P(A)=\delta_a(A)= \begin{cases} 1, & a\in A\\ 0, & a\not\in A \end{cases} \end{equation}

    で定義する． これは

    \begin{align} &(\text{\(a\)が抜き出される確率})=1\\ &(\text{\(\Omega-{a}\)の点が抜き出される確率})=0 \end{align}

    であるから，\(\Omega\) から1点抜き出すと それは ほとんど確実に \(a\) であるような 抜き出しを考えていることになる．


確率密度が定義されない例 (その2)

  • 有理数の抜き出し

    有理数 \(\mathbb{Q}_{[0,1]}\) 全体に番号をふり， これを \(q_{1},q_{2},\dotsc\) で表す．

    \begin{equation} P(A)=\sum_{i:q_i\in A}2^{-i} \end{equation}

    という確率測度を考える． 例えば

    \begin{equation} P(\mathbb{Q}_{[0,1]})=1,\quad P(\Omega-\mathbb{Q}_{[0,1]})=0 \end{equation}

    である．


この確率測度においては確率密度を考えることができない． なぜなら1点 \(q_i\) の起こる確率は

\begin{equation} P\{q_i\}=2^{-i} \end{equation}

であるので， 密度関数 \(f\) は

\begin{equation} P\{q_i\}=\int_{\{q_i\}}f(x)\mu(dx) =f(q_i)\times\mu(q_i)=2^{-i} \end{equation}

とならなくてはいけないが， 1点の Lebesgue 測度は0なので

\begin{equation} f(q_i)\times\mu(q_i) =f(q_i)\times0=0 \end{equation}

となり， \(f\) を構成することは不可能である．


演習


練習問題

  • 正規分布の確率密度関数

    \begin{equation} f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} \end{equation}

    が \((-\infty,\infty)\) で積分すると1となることを確かめよ.

  • 次の関数が確率密度となるように \(a\) を定めよ．

    \begin{equation} h(x)=a\exp(-4x^{2})\quad(-\infty < x < \infty) \end{equation}

今回のまとめ

  • 確率密度
    • 確率密度の積分による確率測度の表現
    • 確率密度の満たすべき条件
    • Riemann 積分と Lebesgue 積分
    • いろいろな確率分布