一般の確率空間
確率・統計 - 第2講
(Press ? for help, n and p for next and previous slide)
村田 昇
前回のおさらい
- 有限試行の確率空間
- 確率論の基本用語 : 試行,標本点,標本空間,事象
- 事象は標本空間の部分集合
- 事象の演算は集合の演算と等価
- 確率測度の基本的な性質(正値性,加法性,全確率)
- 確率空間は標本空間,事象の集合,確率測度の3つ組
有理数の可算性
可算集合
定義
集合の全ての要素に自然数で順番に番号が与えられることを 可算 (可付番) (enumerable, countable) という.
- 自明な可算集合の例
- 要素が有限個の集合
- 自然数
有理数の可算性
区間 \((0,1)\) に含まれる全ての有理数は可算
- 有理数と自然数に1対1の対応があることを示せばよい
分子\分母 2 3 4 5 6 \(\cdots\) 1 1/2 1/3 1/4 1/5 1/6 \(\cdots\) 2 2/3 2/42/5 2/6\(\cdots\) 3 3/4 3/5 3/6\(\cdots\) 4 4/5 4/6\(\cdots\) 5 5/6 \(\cdots\) \(\vdots\) \(\cdots\) - 対応づけ出来そうだが規則の記述は難しそう
Bernsteinの定理
- 1対1の対応が存在することを示す代わりに, \(A\)と\(B\)の部分集合, および \(A\)の部分集合と\(B\)の間に それぞれ1対1の対応が存在することを示せばよい.
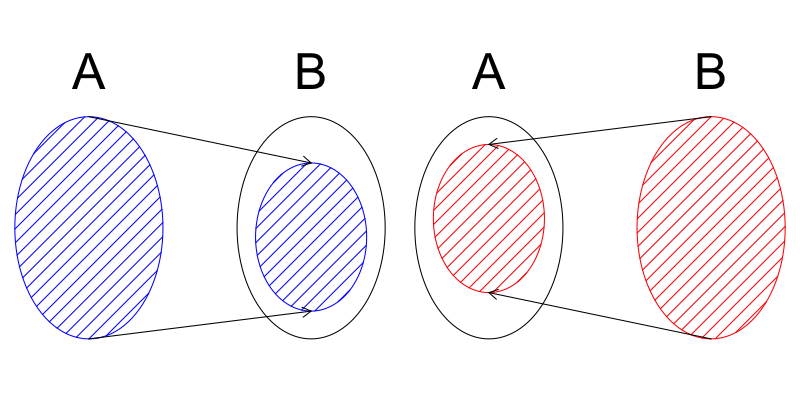
Figure 1: Bernsteinの定理
有理数の可算性 (再考)
- Bernstein の定理を用いた場合
全ての自然数 \(n\) から有理数の部分集合 \(1/q\) への1対1対応
\begin{equation} n\mapsto \frac{1}{q}=\frac{1}{n+1} \end{equation}(有理数としては \(1/q\) の形しか用いない)
全ての有理数 \(p/q\) から自然数 \(n\) の部分集合への1対1対応
\begin{equation} \frac{p}{q} \mapsto n=2^{p}\times 3^{q} \end{equation}(自然数としては2と3の倍数しか用いない)
演習
練習問題
- 整数が可算であることを示せ.
- 自然数の組 \((m,n)\) が可算であるかどうか論じよ.
- 1以上の有理数が可算であるかどうか論じよ.
無理数の非可算性
非可算集合
定義
可算でないことを 非可算 (unenumerable, uncountable) という.(不可算と書かれている場合もある)
- 非可算集合の例
- 区間 \((0,1)\) に含まれる無理数
- 実数全体
Cantorの対角線論法
- 無理数の非可算性の証明 (背理法)
- 証明の概要 (詳しくは講義資料)
その1
区間 \((0,1)\) に含まれる 無理数の集合は可算 と仮定する.
その2
有理数の集合は可算なので, 仮定より無理数と有理数の和である実数も可算となる.
- 証明 (つづき)
その3
自然数との対応付けを行い,番号順に並べる.
\begin{equation} \begin{array}{cc@{\,}c@{\,}c@{\,}c@{\,}c@{\,}c} 1:&0.&d^{1}_{1}&d^{1}_{2}&d^{1}_{3}&d^{1}_{4}&\dotsm\\ 2:&0.&d^{2}_{1}&d^{2}_{2}&d^{2}_{3}&d^{2}_{4}&\dotsm\\ 3:&0.&d^{3}_{1}&d^{3}_{2}&d^{3}_{3}&d^{3}_{4}&\dotsm\\ 4:&0.&d^{4}_{1}&d^{4}_{2}&d^{4}_{3}&d^{4}_{4}&\dotsm\\ \vdots&&&\vdots \end{array} \end{equation}ただし,有限桁の小数の場合は \(0\) で埋める.
- 証明 (つづき)
その4
第n番の数の第n桁目 \(d^{n}_{n}\) とは 異なる数 \(\tilde{d}^{n}_{n}\not=d^{n}_{n}\) を選び,これらを並べた次の数を考える.
\begin{equation} \begin{array}{c@{\,}c@{\,}c@{\,}c@{\,}c@{\,}c} 0.&\tilde{d}^{1}_{1}&\tilde{d}^{2}_{2}&\tilde{d}^{3}_{3}&\tilde{d}^{4}_{4} &\dotsm \end{array} \end{equation}その5
区間 \((0,1)\) に含まれるこの数の番号を探す.
その6
第n番の数とは第n桁目が 違っている ので, この数は区間 \((0,1)\) の 全ての実数を並べたはずの表にはない .
- 証明 (つづき)
その7
番号が振られていない数が存在するので 区間 \((0,1)\) の実数が可算である (並べて番号が付けられる)ことに矛盾する.
その8
つまり最初の仮定 “無理数の集合は可算” が間違っていたということ.
集合の分類
- 無限集合を更に分類(可算と非可算)する必要がある
- 集合の濃度
- この講義で必要な概念は以下の3つ
- 有限の濃度
- 有限個の要素からなる集合
- 可算の濃度
- 自然数,有理数など
- 連続の濃度
- 無理数,実数など
- この講義で必要な概念は以下の3つ
- より詳しくは位相と集合の本を参照
演習
練習問題
- 以下の集合の濃度を答えなさい.
- 区間 \((0,1)\) に含まれる有理数
- 区間 \((0,1)\) に含まれる無理数
- 実数 \(\mathbb{R}\) (区間 \((-\infty,\infty)\))
- 2つの実数の組 \((x,y)\in\mathbb{R}^{2}\)
- 2次元空間で \(xy\) 座標がともに整数となる点の集合
- 表が出るまでコインを投げ続ける試行の標本空間
一般の確率測度
可測集合
- 可測集合 (measurable set)
- 確率測度 \(P\) で確率の値を測ることができる集合
(標本点の集合の中で事象として考えてよいもの) - 可測 (measurable)
- “集合 \(A\) が可測”とは 集合 \(A\) を確率測度 \(P\) で測ることができること
集合族
- 確率測度 \(P\) で確率の値を測ることができる 対象全体 (関数 \(P\) の 定義域) を \(\mathcal{F}\) と書く
- 定義域 \(\mathcal{F}\) は 可測な事象(標本空間の部分集合) \(A\subset\Omega\) の集まり
- このような“集合の集合”を 集合族 (family of sets) という
\(\sigma\)-加法族
定義
以下の (\(\sigma.1\))-(\(\sigma.3\)) の3つの条件を満たす集合族を \(\sigma\)-加法族 (\(\sigma\)-algebra) と呼ぶ.
\begin{align} (\sigma.1)\quad &\Omega\in\mathcal{F}\\ (\sigma.2)\quad &A\in\mathcal{F} \Rightarrow A^c\in\mathcal{F}\\ (\sigma.3)\quad &A_n\in\mathcal{F},\; (n=1,2,\dotsc) \Rightarrow \bigcup_{n=1}^\infty A_n\in\mathcal{F} \end{align}- (\(\sigma.1\))-(\(\sigma.3\)) は 定義域 \(\mathcal{F}\) の満たすべき条件でもある
条件の意味
- (\(\sigma.1\))
- 標本空間(全事象)は可測である( \(P\) で測ることができる)
- (\(\sigma.2\))
- ある事象が可測なら,その余事象も可測である
- (\(\sigma.3\))
- 可測集合の可算(自然数で番号付けできる)無限和も可測である
確率測度
定義
集合関数 \(P\) は条件(P.1), (P.2)を満たすとき 測度 (measure) と呼ばれ, さらに(P.3)まで満たすとき 確率測度 (probability measure) と呼ばれる. また \(P(A)\) を \(A\) の 測度 という.
\begin{align} (P.1)\quad &P(A)\ge 0,\; A\in\mathcal{F}\\ (P.2)\quad &P\biggl(\sum_{n=1}^\infty A_n\biggr) =\sum_{n=1}^\infty P(A_n),\; A_n\in\mathcal{F}\\ (P.3)\quad &P(\Omega)=1 \end{align}- (P.2)を \(\sigma\)-加法性 (\(\sigma\)-additivity) という
確率空間
定義
標本空間 \(\Omega\) と確率測度 \(P\) , および \(P\) の定義域である \(\sigma\)-加法族 \(\mathcal{F}\) の組 \((\Omega,\mathcal{F},P)\) を 確率空間 (probability spcae) という.
Lebesgue 測度
ルーレット回しの確率測度
区間 \((0,1]\) からの無作為抽出
試行 \(T\) を “区間 \((0,1]\) から無作為に一点抜き出すこと” とする. このとき標本空間は
\begin{equation} \Omega=(0,1] \end{equation}であり無限試行となる. 確率測度は事象 \(A\) が 区間 \([a,b]\), \((a,b)\), \([a,b)\) または \((a,b]\) といった簡単な集合であれば
\begin{equation} P(A)=|A|=b-a,\;\text{(\(|A|\)は区間の長さを表す)} \end{equation}とすればよい.
確率測度の定義域
- 確率測度 \(P\) の定義域 \(\mathcal{F}\) は 集合演算で作られる
可算個 の区間を組み合わせてつくられる集合
\begin{align} \mathcal{F} &=\{\text{可算個の任意の区間の和,差,交,}\\ &\qquad\qquad\qquad\text{余集合から作られる集合}\} \end{align}- 集合の測度(確率)は (P.2) の性質より 排反な区間の長さの和から計算できる
Lebesgue 測度
定義
“区間 \((0,1]\) から無作為に一点抜き出す”試行 \(T\) によって考えられる確率測度 \(P\) を \((0,1]\) 上の Lebesgue 測度 (Lebesgue measure) という. また Lebesgue 測度の定義域となる \(\sigma\)-加法族を \(\mathbb{R}\) の Borel 集合族 (Borel field) という.
- Lebesgue 測度は \(\mu\) で表されることが多い
- 厳密な定義については Lebesgue 積分の本を参照
Lebesgue 測度の計算
一点が抜き出される確率
Lebesgue 測度において, \(P\{a\}\) (一点 \(a\) が抜き出される確率)は \(0\) となる.
例えば \(\{1,1/2,1/3,\dotsc\}\) という可算集合を考えると,
\begin{equation} P\left\{\frac{1}{n}\right\}\ge\varepsilon>0 \Rightarrow P\left(\left\{1,\frac{1}{2},\frac{1}{3},\dotsc\right\}\right) =\sum_{n=1}^\infty P\left\{\frac{1}{n}\right\} % \ge\sum_{n=1}^\infty\varepsilon \to\infty \end{equation}となり矛盾が生じる.
抜き出した点が有理数である確率
\begin{align} \mathbb{R}_{(0,1]}&=\{\text{区間\((0,1]\)上の実数全体}\}(=\Omega)\\ \mathbb{Q}_{(0,1]}&=\{\text{区間\((0,1]\)上の有理数全体}\} \end{align}と書くことにする. 有理数は 可算 であるからその要素に番号が付けられ,
\begin{equation} \mathbb{Q}_{(0,1]}=\{q_1,q_2,q_3,\dotsc,q_n,\dotsc\} \end{equation}と書けるので,(P.2)の性質により計算できる.
\begin{align} P(\mathbb{Q}_{(0,1]}) &=P\left(\{q_1,q_2,q_3,\dotsc,q_n,\dotsc\}\right)\\ &=P\{q_1\}+P\{q_2\}+P\{q_3\}+\dotsb+P\{q_n\}+\dotsb\\ &=0+0+0+\dotsb+0+\dotsb =0 \end{align}
抜き出した点が無理数である確率
\begin{equation} \text{(区間\((0,1]\)上の無理数全体)}=\mathbb{R}_{(0,1]}-\mathbb{Q}_{(0,1]} \end{equation}を用いて求められる.
\begin{equation} P(\mathbb{R}_{(0,1]}-\mathbb{Q}_{(0,1]}) =P(\mathbb{R}_{(0,1]})-P(\mathbb{Q}_{(0,1]})=1-0=1 \end{equation}無理数全体は 可算でない ため有理数のように成分毎の可算無限和では書けず, したがって(P.2)の性質を使って計算することはできない.
異なる区間の場合
“区間 \((0,5]\) から無作為に一点抜き出す”試行を考えたとき, その標本空間は \(\Omega=(0,5]\) となる. この試行の確率測度は Lebesgue 測度 \(\mu\) を定数倍(正規化)し,
\begin{equation} P(A)=\frac{\mu(A)}{\mu(\Omega)}=\frac{\mu(A)}{5},\;A\in\mathcal{F} \end{equation}とすることによって構成できる.
零集合
定義
空集合でない集合 \(A\) で その事象が起こる確率が \(P(A)=0\) となるものがある. こうした集合を 零集合 (null set) と呼ぶ.
- 以下は等しくないことに注意 (有理数と無理数の例)
- 事象 \(A\) の確率が \(0\) である
- 事象 \(A\) に含まれる標本点が全く起こらない
“ほとんど確実”
確率での特殊な言い回し
事象 \(A=\{\omega|\alpha(\omega)\}\) の確率が1であるとき, “ほとんど確実に (almost surely)” あるいは “条件 \(\alpha(\omega)\) が確率1で成り立つ” といい, 以下のように書く.
\begin{equation} \alpha(\omega)\;\text{a.s.} \end{equation}- 別の表現
- 事象 \(A\) の余事象 \(A^c\) は零集合
- 条件 \(\alpha\) は成り立たないこともあるが,その確率は0
演習
練習問題
- Buffonの針 (Buffon’s needle) の問題を考えよ
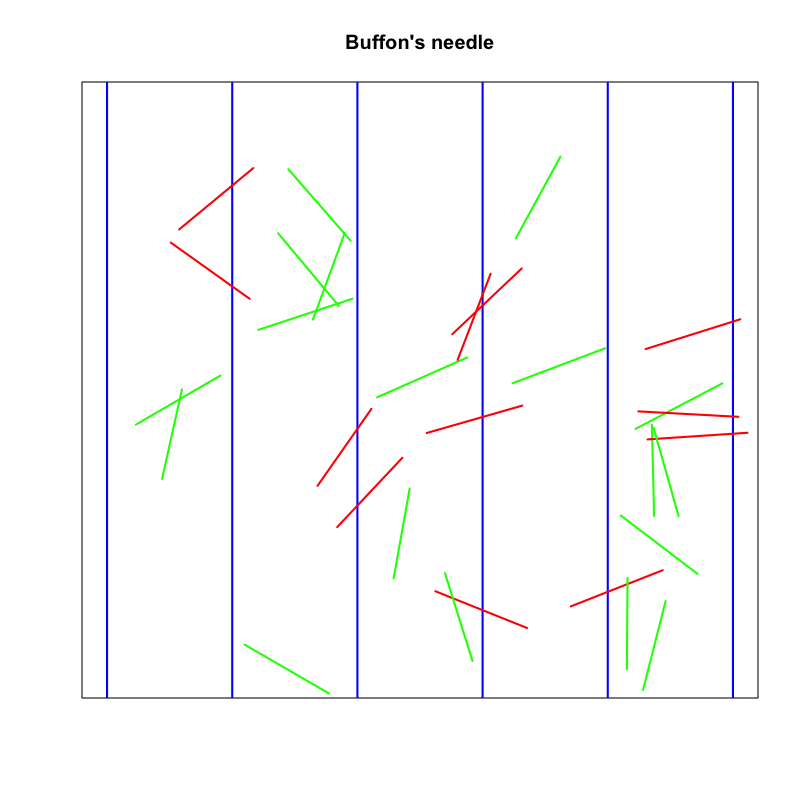
Figure 2: Buffonの針
2次元平面上に等間隔 \(d\) で平行線が引いてある. 長さ \(l\) の針をこの平面上にランダムに落としたとき, 平行線と交わる確率を求めよ.ただし \(l< d\) とする.
今回のまとめ
- 一般の確率空間
- 有限集合と無限集合
- 集合の濃度 (無限集合は更に分類される)
- 可算集合 : 自然数,整数,有理数
- 連続集合 : 無理数,実数
- 一般の確率測度と \(\sigma\)-加法性の関係
- Lebesgue 測度と Borel 集合族 (応用上重要な概念)
- “ほとんど確実に成り立つ”