統計的有意性とp値

検定の基本的な考え方

(Press ? for help, n and p for next and previous slide)

村田 昇

検定の考え方

統計的仮説検定

  • ある現象・母集団に対して仮定された仮説の真偽を データに基づいて統計的に検証する方法
  • 検定の基本的手続き
    1. 帰無仮説(および対立仮説)を立てる
    2. データから計算できる統計量を設定する
      • 検定統計量 という
    3. 帰無仮説のもとで検定統計量が従う標本分布を求める
      • 帰無分布 という
    4. 実際のデータから検定統計量の値を計算する
    5. 計算された検定統計量の値が 仮説が正しいときに十分高い確率で 得られるかどうかを判断する
      • この閾値を 有意水準 という

例題

  • 表の出る確率が高くなるよう細工したコインを見つける問題を考える
    • 何回か投げてみる
    • 表が裏より出やすければ「いかさま」と判断する
    • どのくらい表が出たら怪しいと考えられるだろうか?

問題

  • いかさまのないコイン(表の出る確率が0.5)を20回投げたとき， 表が \(k\) 回出る確率を求めなさい

解答

  • 以下の式で計算される

    \begin{equation} P(\text{表の回数}=k) = \left(20\atop k\right) 0.5^{k} (1-0.5)^{20-k} \end{equation}

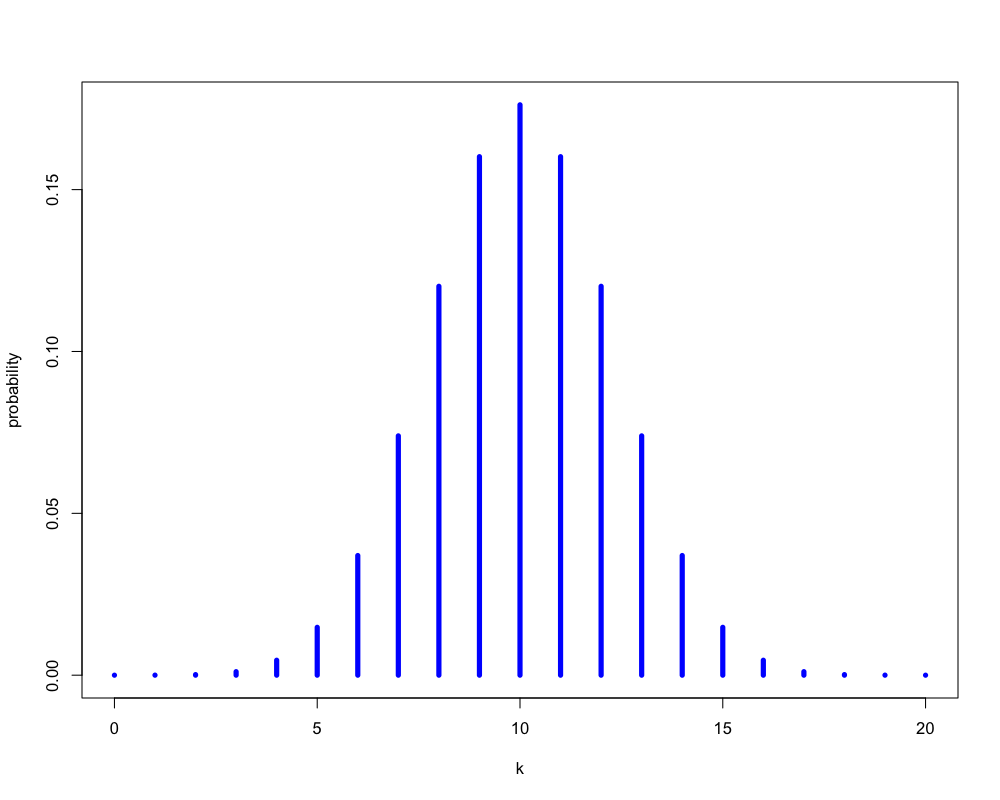
pval_null_n_20.png

Figure 1: いかさまのないコインの場合


問題

  • いかさまのあるコイン(表の出る確率が0.6)を20回投げたとき， 表が \(k\) 回出る確率を求めなさい

解答

  • 以下の式で計算される

    \begin{equation} P(\text{表の回数}=k) = \left(20\atop k\right) 0.6^{k} (1-0.6)^{20-k} \end{equation}

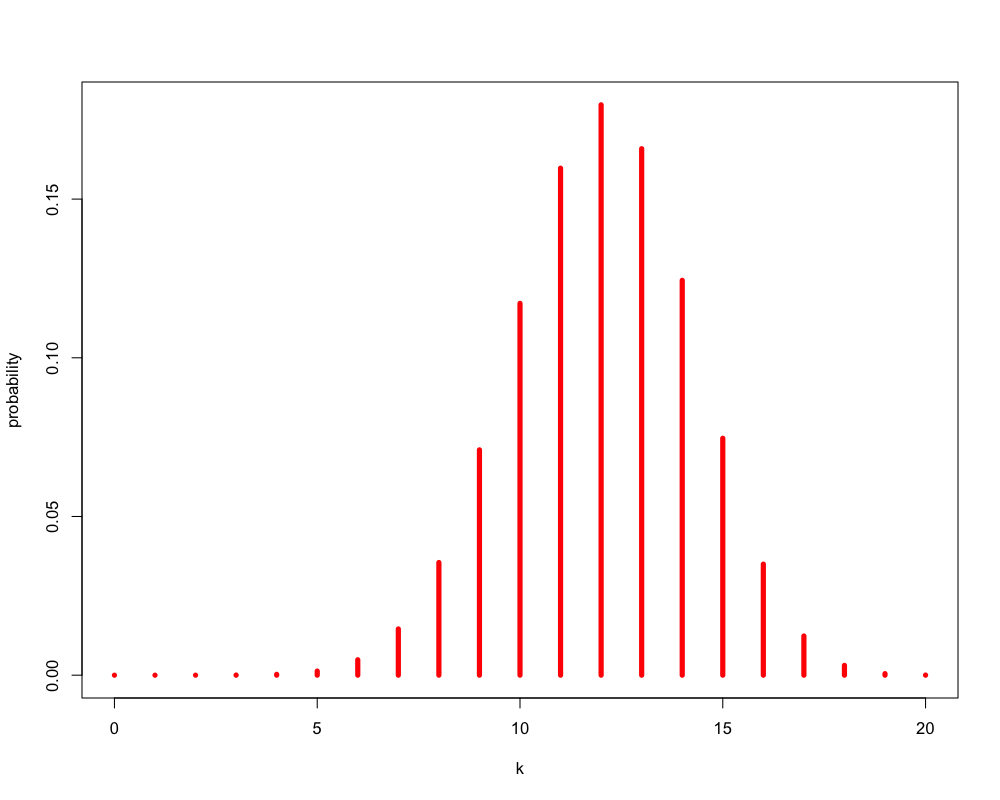
pval_alt_n_20.png

Figure 2: いかさまのあるコインの場合


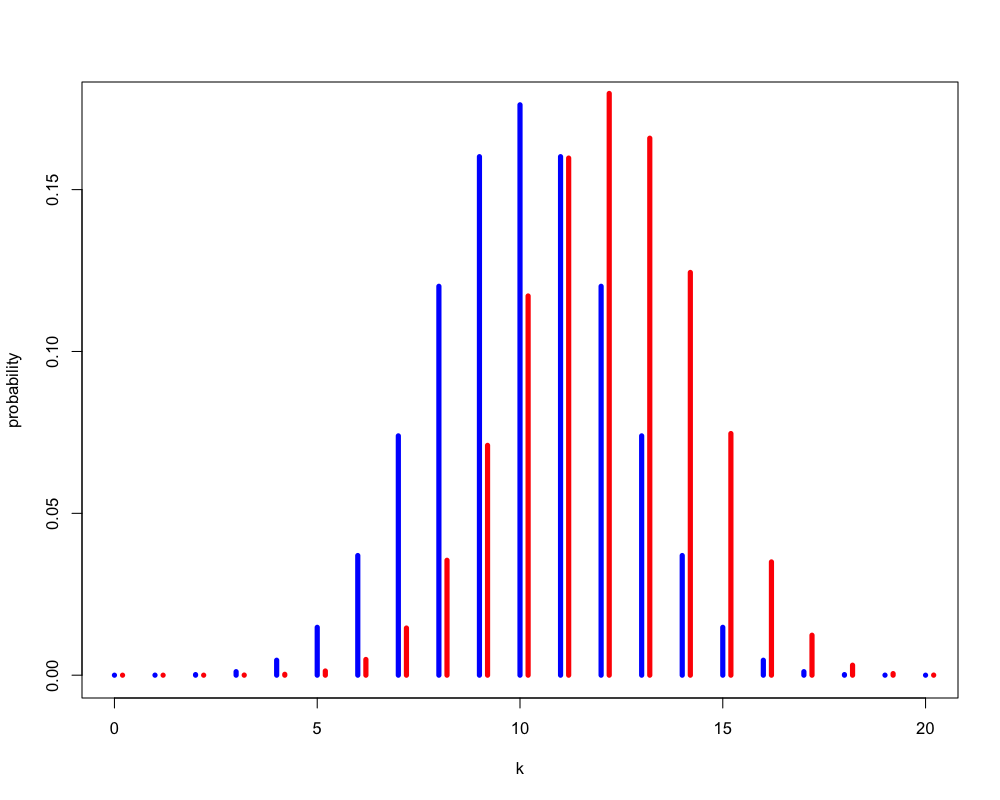
pval_both_n_20.png

Figure 1: いかさまの有無による違い


問題

  • いかさまのないコインを20回投げたとき， 15回以上表が出る確率はいくつか

解答

  • 以下の式で計算される

    \begin{equation} P(\text{表の回数}\ge 15) = \sum_{k=15}^{20}\left(20\atop k\right) 0.5^{k} (1-0.5)^{20-k} = 0.02 \end{equation}
  • 「20回投げて表が出た回数」を検定統計量と考える
  • 「20回投げて15回以上表が出たら怪しい」と考える
    • 怪しいと考える検定統計量の領域を 棄却域 という
  • この方策で「いかさまのないコイン」を間違えて怪しいとしてしまう確率は0.02である
    • 第一種の過誤 (type-I error) という

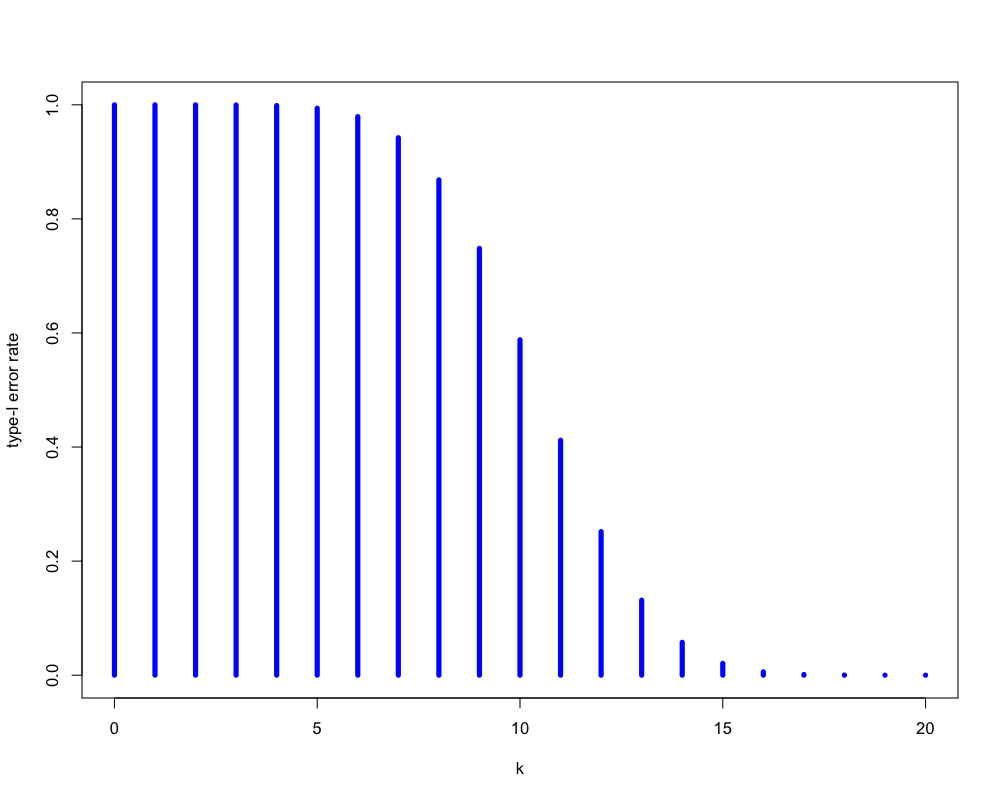
pval_null_cum_n_20.png

Figure 1: いかさまのないコインの場合


問題

  • いかさまのあるコインを20回投げたとき， 15回以上表が出る確率はいくつか

解答

  • 以下の式で計算される

    \begin{equation} P(\text{表の回数}\ge 15) = \sum_{k=15}^{20}\left(20\atop k\right) 0.6^{k} (1-0.6)^{20-k} = 0.13 \end{equation}
    • この方法で「いかさまのあるコイン」を見分けられる確率は13%程度となる
    • これを検出力 (power) という

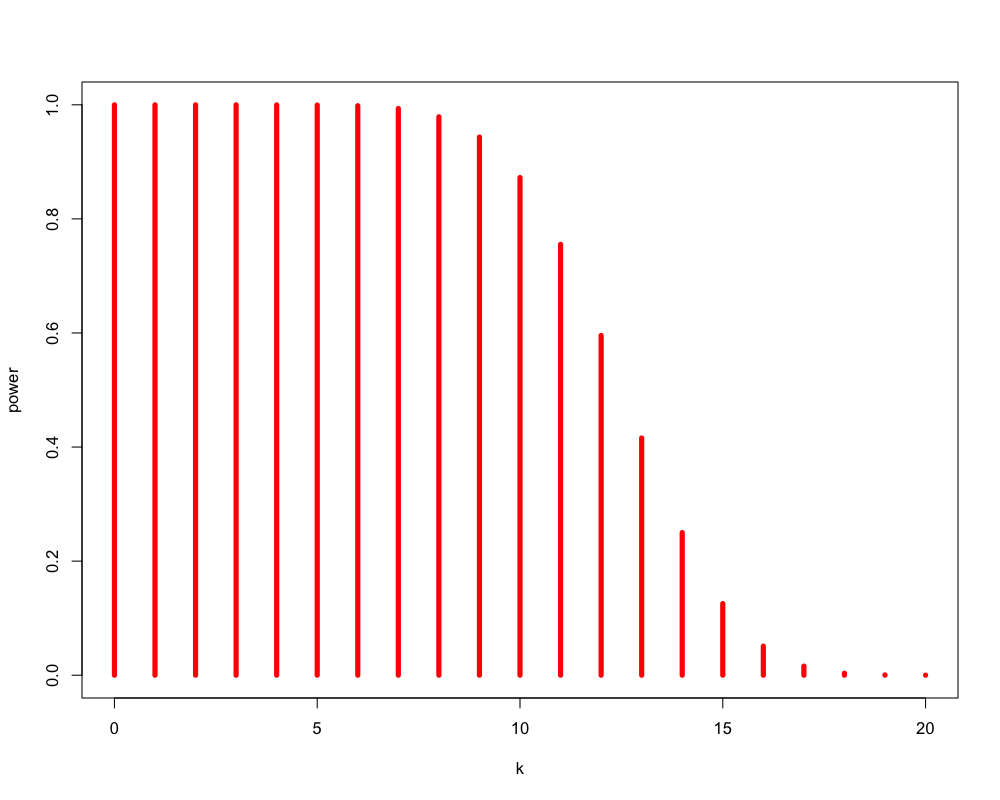
pval_alt_cum_n_20.png

Figure 1: いかさまのあるコインの場合


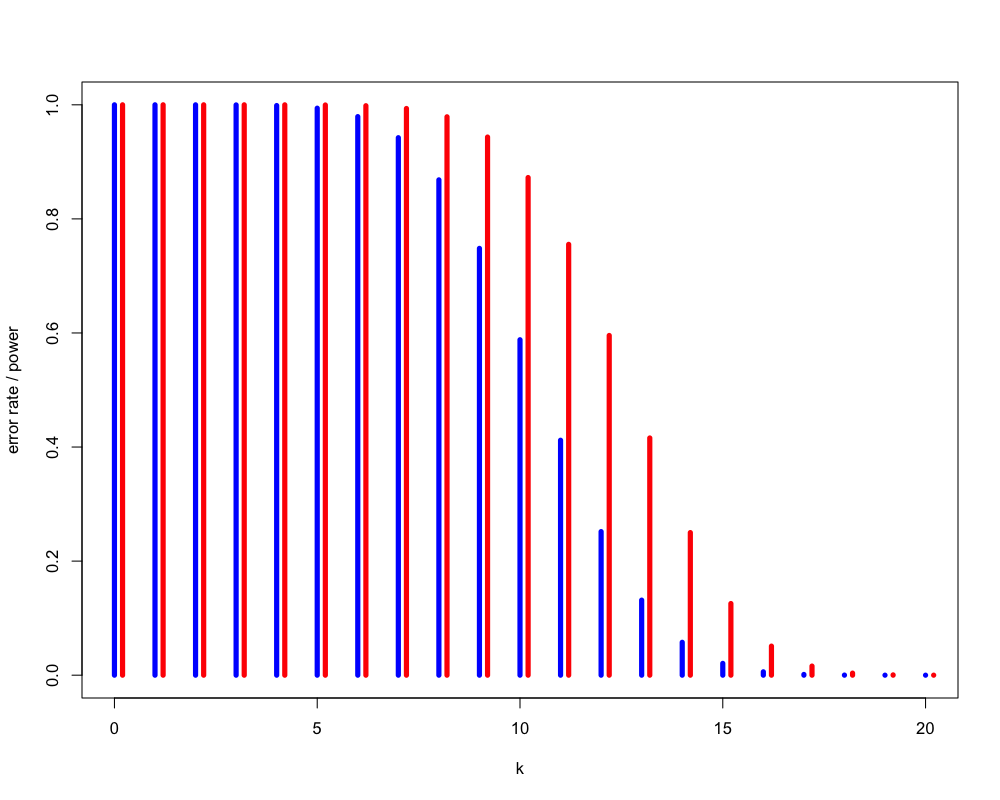
pval_both_cum_n_20.png

Figure 1: いかさまの有無による違い


問題

  • もっとあからさまにいかさまのあるコイン(表の出る確率が0.9)を20回投げたとき， 15回以上表が出る確率はいくつか

解答

  • 以下の式で計算される

    \begin{equation} P(\text{表の回数}\ge 15) = \sum_{k=15}^{20}\left(20\atop k\right) 0.9^{k} (1-0.9)^{20-k} = 0.98 \end{equation}
    • この方法で「あからさまにいかさまのあるコイン」を見分けられる確率は98%程度となる
    • 対立仮説によって検出力は異なる

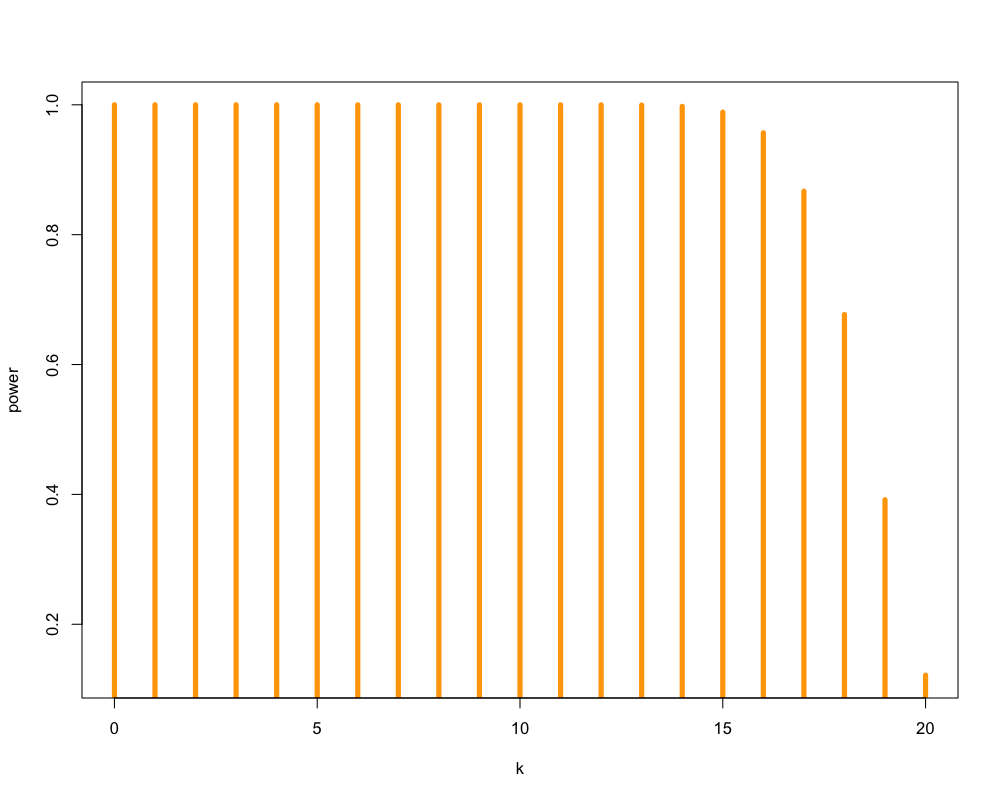
pval_alt2_cum_n_20.png

Figure 1: いかさまのあるコインの場合


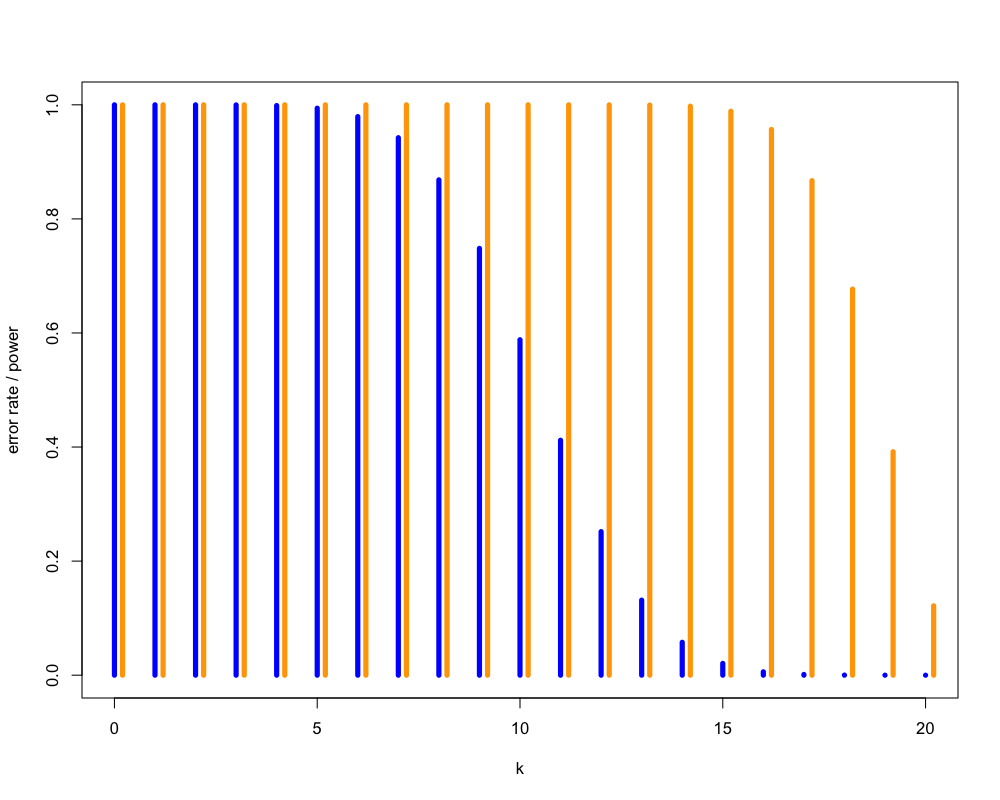
pval_both2_cum_n_20.png

Figure 1: いかさまの有無による違い


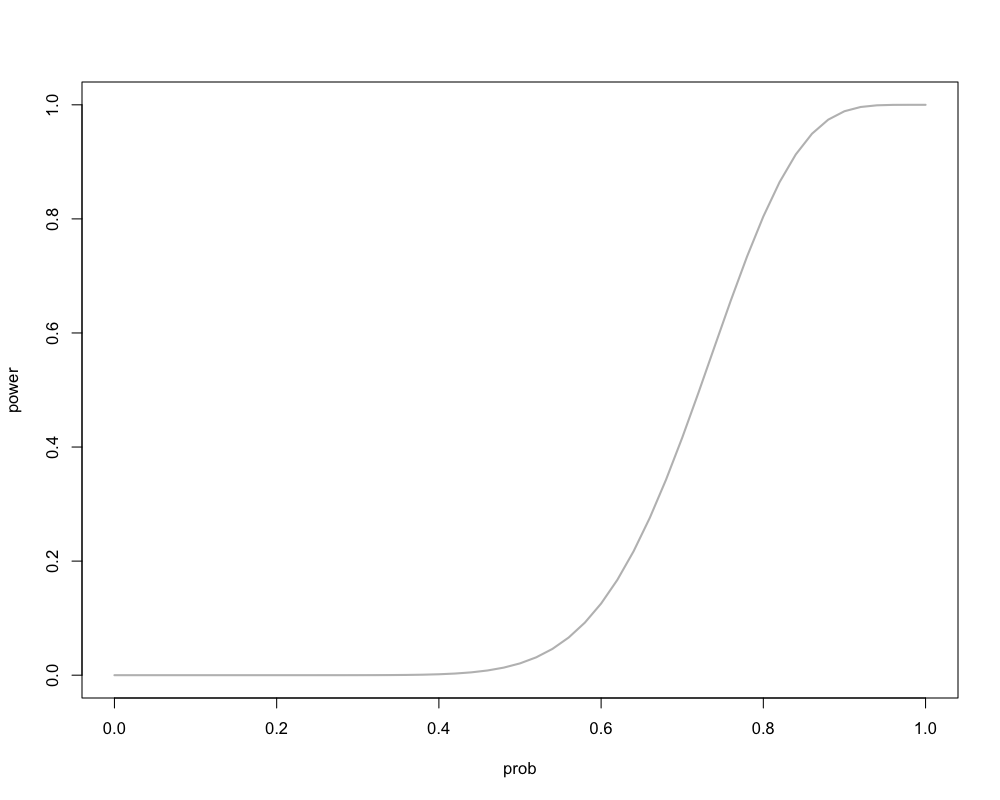
pval_power_n_20.png

Figure 1: 対立仮説による検出力の違い (15回以上をいかさまとする場合)


問題

  • いかさまのないコインを100回投げたとき， 60回以上表が出る確率はいくつか

解答

  • 以下の式で計算される

    \begin{equation} P(\text{表の回数}\ge 60) = \sum_{k=60}^{100}\left(100\atop k\right) 0.5^{k} (1-0.5)^{100-k} = 0.028 \end{equation}
  • 異なる検定統計量「100回投げて表が出た回数」を考えている

問題

  • いかさまのあるコインを100回投げたとき， 60回以上表が出る確率はいくつか

解答

  • 以下の式で計算される

    \begin{equation} P(\text{表の回数}\ge 60) = \sum_{k=60}^{100}\left(100\atop k\right) 0.6^{k} (1-0.6)^{100-k} = 0.543 \end{equation}
    • 同じ仮説だとしても検定統計量によって検出力は異なる．

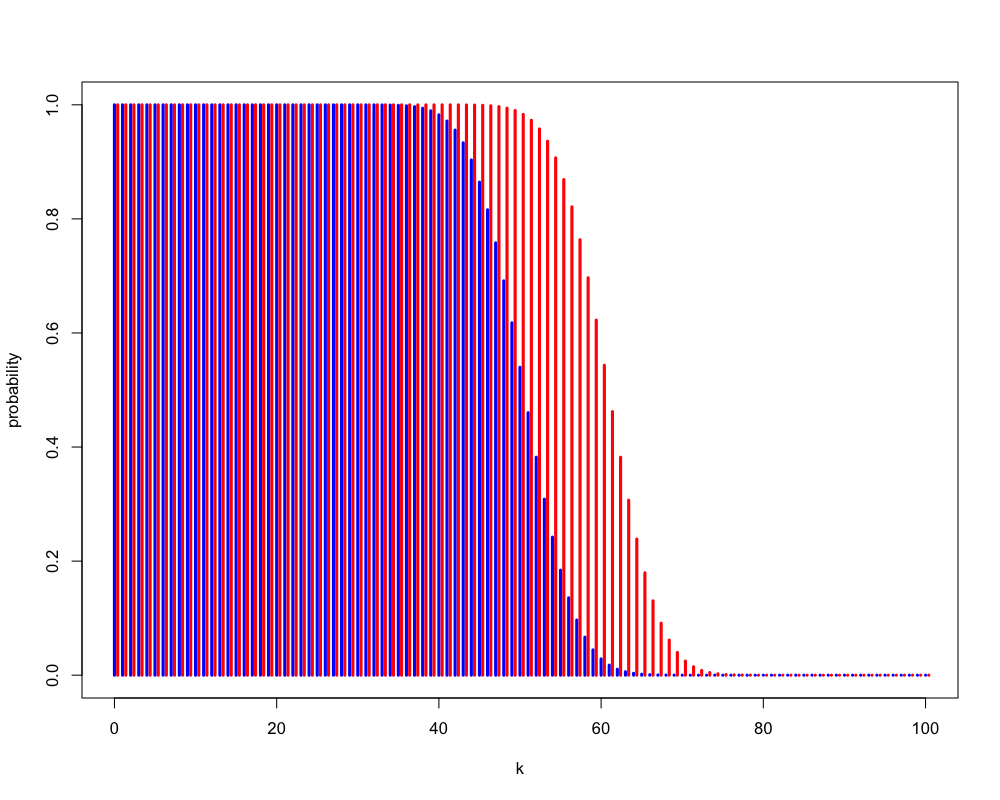
pval_both_cum_n_100.png

Figure 1: いかさまの有無による違い


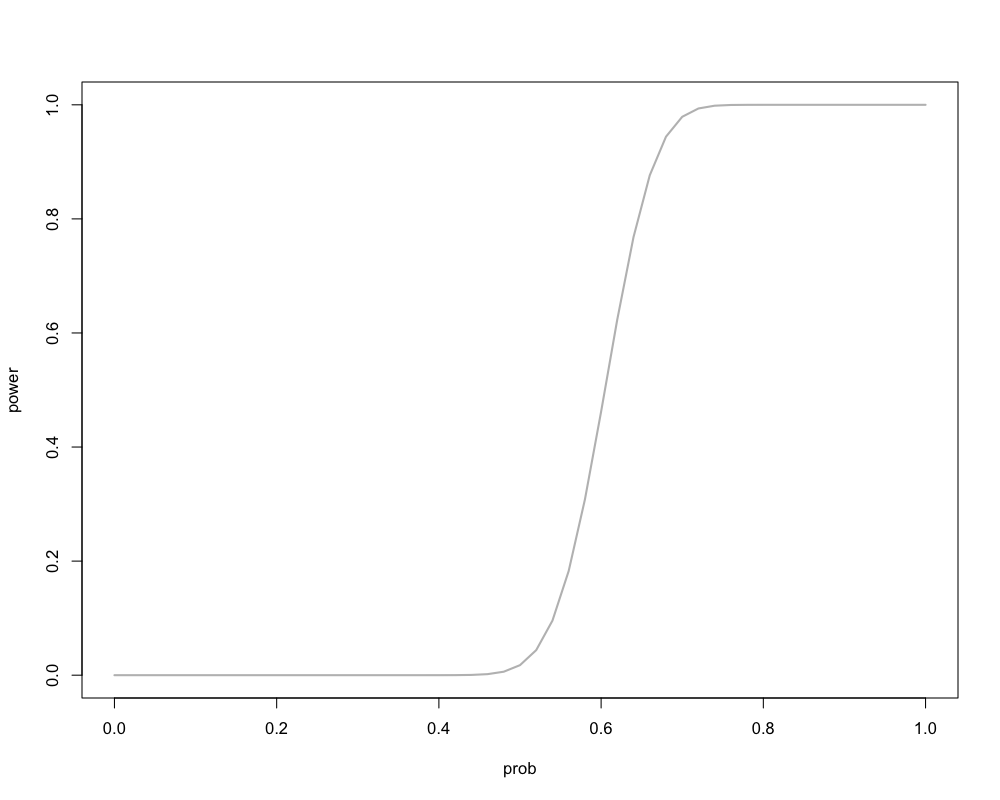
pval_power_n_100.png

Figure 1: 対立仮説による検出力の違い (15回以上をいかさまとする場合)


問題

  • 以下の問に答えなさい
    • 100個のコインがある
    • このうち10個には“あるいかさま”が施されている
    • ある検定統計量を用いて有意水準0.05の検定を考える
    • 設定した検定統計量の検出力は0.8であることがわかっている
    • このときどの程度のいかさまを見破ることができるだろうか?

解答例

  • 以下おおざっぱな考え方を示す
    • いかさまを検出できる確率は0.8なので， 平均的には\(10\times0.8=8\)個の いかさまコインを見付けられる
    • 有意水準0.05なので， 平均的には\(90\times0.05=4.5\)個 誤っていかさまコインだと判定してしまう
    • 見破ったと考える12.5個のうち， 本当にいかさまをしているのは8個なので， 64%しか当たらないことになる
  • 実際の状況に合わせて検定の意味を考える必要がある

p値とその誤解

p値とは

おおざっぱにいうと， p値とは特定の統計モデルのもとで， データの統計的要約 (たとえば，2グループ比較での標本平均の差) が観察された値と等しいか，それよりも極端な値をとる確率である．

  • p値 は観測された値を使った検定の第一種の過誤の確率として定義される

良くある正しくない記述

  • p値は帰無仮説が正しい確率である
  • p値はそのデータが偶然で得られた確率である
  • 検定結果が有意であるので帰無仮説は必ず棄却すべきである
  • 検定結果が有意でないので帰無仮説を必ず採択すべきである
  • 2つのp値を比べてp値が小さい方の効果が大きいと判断する

ASAの提言


提言の要旨

  • その1

    p値はデータと特定の統計モデルが矛盾する程度をしめす指標のひとつである

    • 統計モデルはいくつもの仮定を含む
    • 帰無仮説は仮定の1つにすぎない
    • p値が小さければ
      単に データと帰無仮説の矛盾の程度が大きい ではなく
      統計モデルの仮定のどれかが間違っている

  • その2

    p値は，調べている仮説が正しい確率や，データが偶然のみで得られた確率を測るものではない

    • 誤差をともなってばらつくのはデータである
    • 仮説や真の値は確率的でない
    • p値は仮説やその計算の背後にある仮定に基づいたデータについての一つの記述である

  • その3

    科学的な結論や，ビジネス，政策における決定は，p値がある値を超えたかどうかにのみ基づくべきではない

    • データ解析や科学的推論を機械的で明白なルールに貶めるようなやり方は 誤った思い込みや貧弱な意思決定につながる
    • 科学的推論には研究デザイン，測定の室，外部のエビデンス，データ解析の背後にある 仮定の妥当性が重要である

  • その4

    適正な推測のためには，すべてを報告する透明性が必要である

    • p値や関連する解析は選択して報告してはいけない
    • 研究の中で調べる仮説の数，データの選択基準，実行したすべての統計解析，計算したすべてのp値を開示すべきである

  • その5

    p値や統計的有意性は，効果の大きさや結果の重要性を意味しない

    • 統計的に有意であることは科学的に意味にあることと同じではない
    • どんなに小さな効果でもサンプルサイズが大きかったり測定精度が十分高ければ小さなp値になるし，その逆もある
    • 効果の推定値が同じ大きさでも，推定の精度が異なれば異なったp値となる

  • その6

    p値は，それだけでは統計モデルや仮説に関するエビデンスの，よい指標とはならない

    • 背景情報や外部のエビデンスがなければ，p値は限られた情報しか提供しない
    • p値が大きくても帰無仮説を好む証拠とはならない
    • p値を計算したらデータ解析は終わりではない