時系列解析

モデルの推定と予測

(Press ? for help, n and p for next and previous slide)

村田 昇

講義の内容

  • 第1回 : 時系列の基本モデル
  • 第2回 : モデルの推定と予測

時系列解析の復習

時系列解析とは

  • 時系列データ
    • 時間軸に沿って観測されたデータ
    • 観測の順序に意味がある
    • 異なる時点間での観測データの従属関係が重要
    • 独立性にもとづく解析は行えない
      • そのままでは大数の法則や中心極限定理は使えない
  • 時系列解析の目的
    • 時系列データの特徴を効果的に記述すること
    • 時系列モデルの推定と評価

時系列モデルと定常性

  • 確率過程

    時間を添え字として持つ確率変数列

    \begin{equation} X_{t},\;t=1,\dotsc,T \end{equation}
  • 弱定常過程 : 以下の性質をもつ確率過程 \(X_t\)
    • \(X_{t}\)の平均は時点\(t\)によらない
    • \(X_{t}\)と\(X_{t+h}\)の共分散は時点\(t\)によらず時差\(h\)のみで定まる
    • 特に\(X_{t}\)の分散は時点\(t\)によらない (\(h=0\)の場合)
  • 多くの場合，弱定常性を考えれば十分なので 単に 定常 ということが多い
  • 定常でない確率過程は 非定常 であるという

ホワイトノイズ

  • 定義

    平均\(0\)，分散\(\sigma^{2}\) である確率変数の 確率分布\(P\)からの 独立かつ同分布な確率変数列

    \begin{equation} X_{t} = \epsilon_{t}, \quad \epsilon_{t} \overset{i.i.d.}{\sim} P \end{equation}
    • 記号 \(\mathrm{WN}(0,\sigma^{2})\) で表記
    • 定常 な確率過程

トレンドのあるホワイトノイズ

  • 定義

    \(\mu,\alpha\) を定数として

    \begin{equation} X_{t}=\mu+\alpha t+\epsilon_{t}, \quad \epsilon_{t} \sim \mathrm{WN}(0,\sigma^2) \end{equation}

    で定義される確率過程

    • 非定常 な確率過程
    • トレンド項(平均値の変化)は現象に応じて一般化される

ランダムウォーク

  • 定義

    \(X_0\) を定数もしくは確率変数として

    \begin{equation} X_{t}=X_{t-1}+\epsilon_{t}, \quad \epsilon_{t} \sim \mathrm{WN}(0,\sigma^2) \end{equation}

    で帰納的に定義される確率過程

    • 分散が時間とともに増加・記憶のあるモデル
    • 非定常 な確率過程

自己回帰過程

  • 定義 (次数\(p\)のARモデル)

    \(a_1,\dotsc,a_p\)を定数とし， \(X_1,\dotsc,X_p\)が初期値として与えられたとき，

    \begin{equation} X_{t}=a_1X_{t-1}+\cdots+a_pX_{t-p}+\epsilon_{t}, \quad \epsilon_{t} \sim \mathrm{WN}(0,\sigma^2) \end{equation}

    で帰納的に定義される確率過程

    • ランダムウォークの一般化
    • 無限長の記憶のある(忘却しながら記憶する)モデル
    • 定常にも非定常にもなる

移動平均過程

  • 定義 (次数\(q\) のMAモデル)

    \(b_1,\dotsc,b_q\)を定数とし， \(X_1,\dotsc,X_q\)が初期値として与えられたとき

    \begin{equation} X_{t} = b_1\epsilon_{t-1}+\cdots+b_q\epsilon_{t-q}+\epsilon_{t}, \quad \epsilon_{t} \sim \mathrm{WN}(0,\sigma^2) \end{equation}

    で定義される確率過程

    • 有限長の記憶のあるモデル
    • 定常 な確率過程

自己回帰移動平均過程

  • 定義 (次数\((p,q)\)のARMAモデル)

    \(a_1,\dotsc,a_p,b_1,\dotsc,b_q\) を定数とし， \(X_1,\dotsc,X_{\max\{p,q\}}\) が初期値として与えられたとき

    \begin{align} X_{t} &= a_1X_{t-1}+\cdots+a_pX_{t-p}\\ &\quad+ b_1\epsilon_{t-1}+\cdots+b_q\epsilon_{t-q} +\epsilon_{t},\\ &\quad \epsilon_{t} \sim \mathrm{WN}(0,\sigma^2) \end{align}

    で帰納的に定まる確率過程

    • AR・MAモデルの一般化・基本的な時系列モデル
    • 定常にも非定常にもなる

自己共分散・自己相関

  • 弱定常な確率過程 : \(X_{t},\;t=1,\dotsc,T\)

    • \(X_{t}\) と \(X_{t+h}\) の共分散は時点\(t\)によらずラグ\(h\)のみで定まる

      自己共分散 (定常過程の性質よりラグは\(h\ge0\)を考えればよい)

      \begin{equation} \gamma(h) = \mathrm{Cov}(X_{t},X_{t+h}) \end{equation}

    • \(X_{t}\) と \(X_{t+h}\) の相関も\(t\)によらずラグ\(h\)のみで定まる

      自己相関

      \begin{equation} \rho(h) =\gamma(h)/\gamma(0) = \mathrm{Cov}(X_{t},X_{t+h})/\mathrm{Var}(X_{t}) \end{equation}
  • 異なる時点間での観測データの従属関係を要約するための最も基本的な統計量

標本自己共分散・標本自己相関

  • 観測データ \(X_1,\dotsc,X_{T}\) からの推定

    • ラグ\(h\)の自己共分散の推定 : 標本自己共分散

      \begin{equation} \hat\gamma(h) = \frac{1}{T}\sum_{t=1}^{T-h}(X_{t}-\bar{X})(X_{t+h}-\bar{X}) \end{equation}

      \(\bar{X}=\frac{1}{T}\sum_{t=1}^TX_{t}\) は標本平均

    • ラグ\(h\)での自己相関の推定 : 標本自己相関

      \begin{equation} \hat\gamma(h)/\hat\gamma(0) = \frac{\sum_{t=1}^{T-h}(X_{t}-\bar{X})(X_{t+h}-\bar{X})}{\sum_{t=1}^T(X_{t}-\bar{X})^2} \end{equation}

13_ar.png

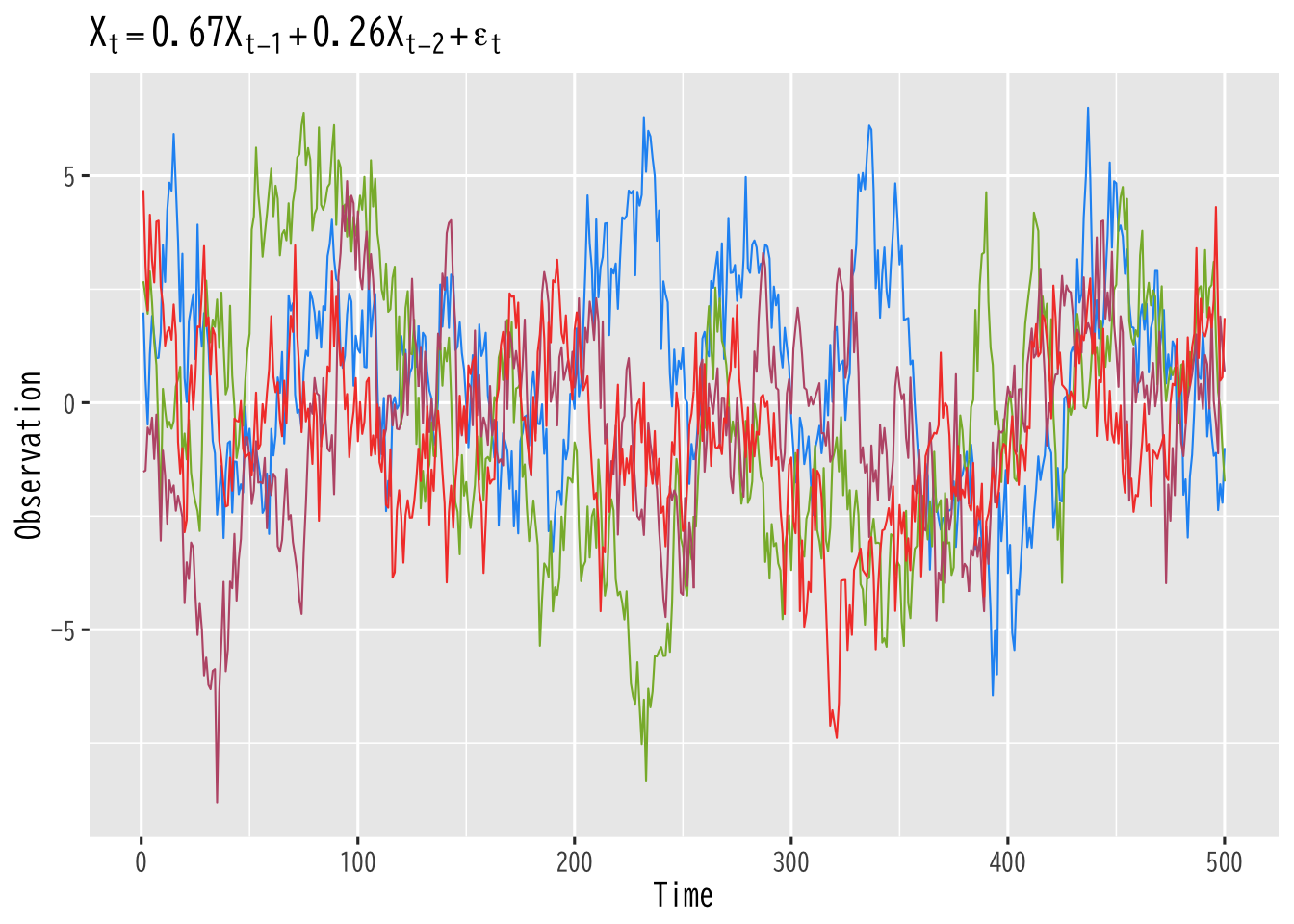
Figure 1: 同じモデルに従うAR過程の例

13_aracf.png

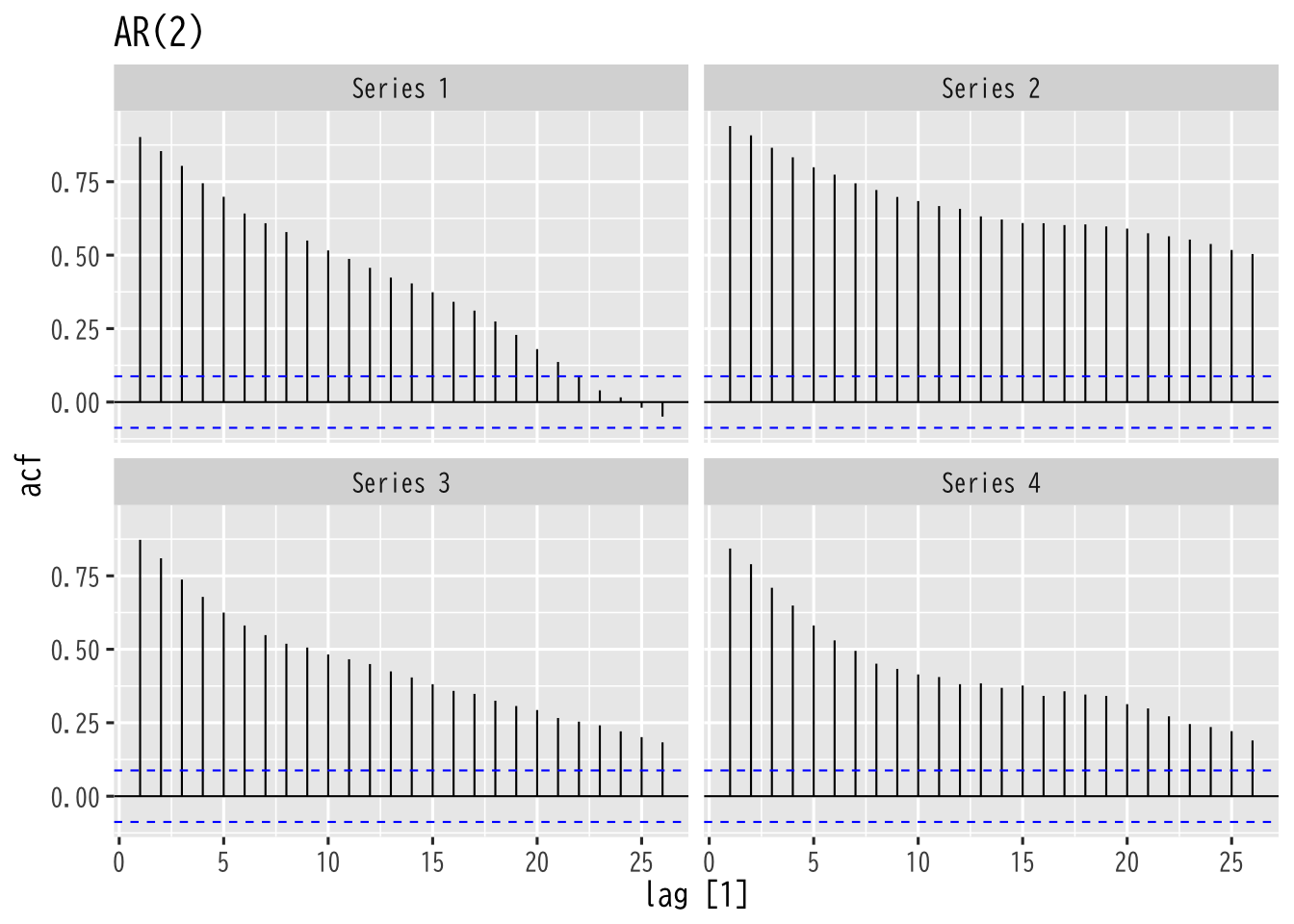
Figure 2: AR過程の自己相関

13_ma.png

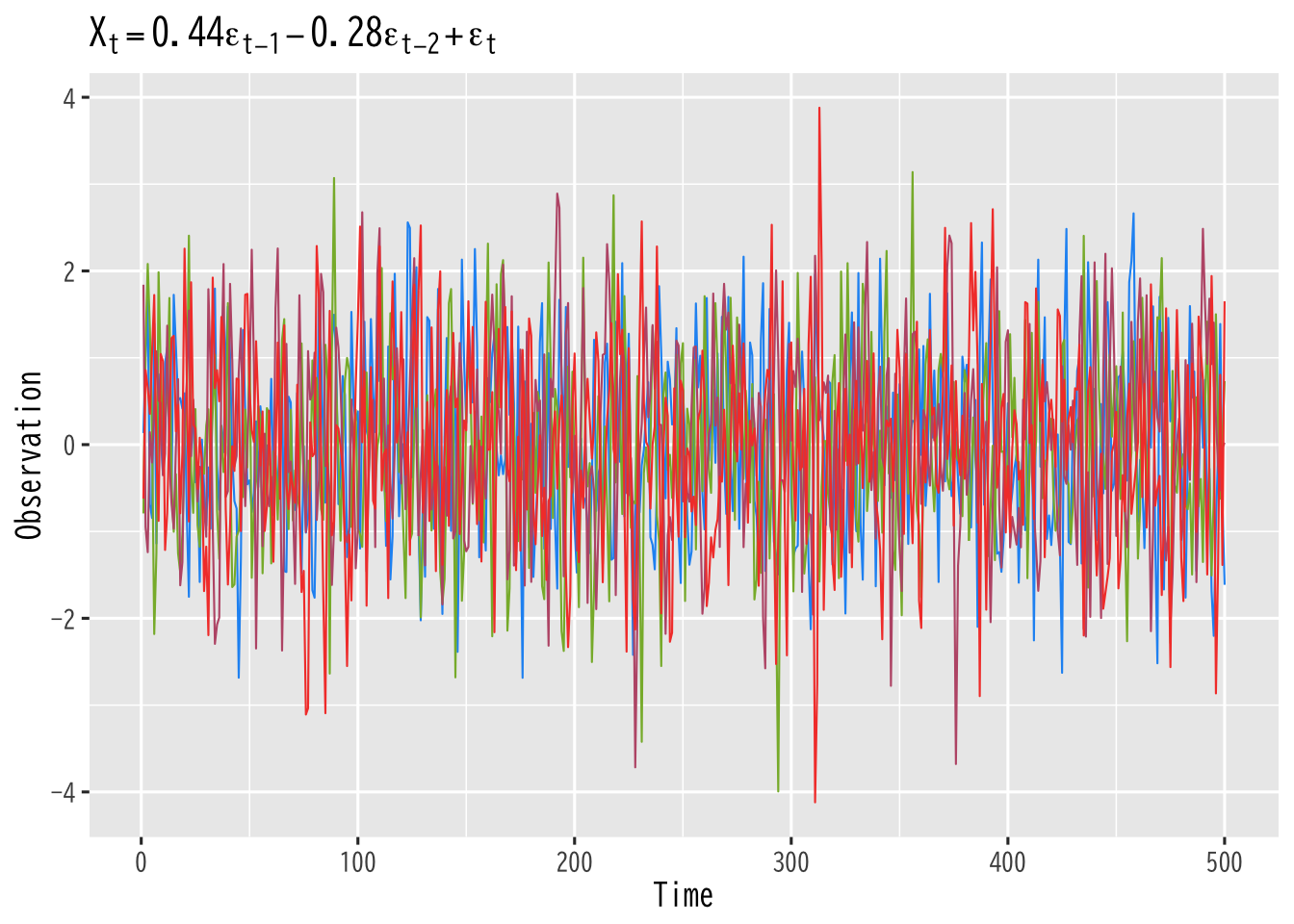
Figure 3: 同じモデルに従うMA過程の例

13_maacf.png

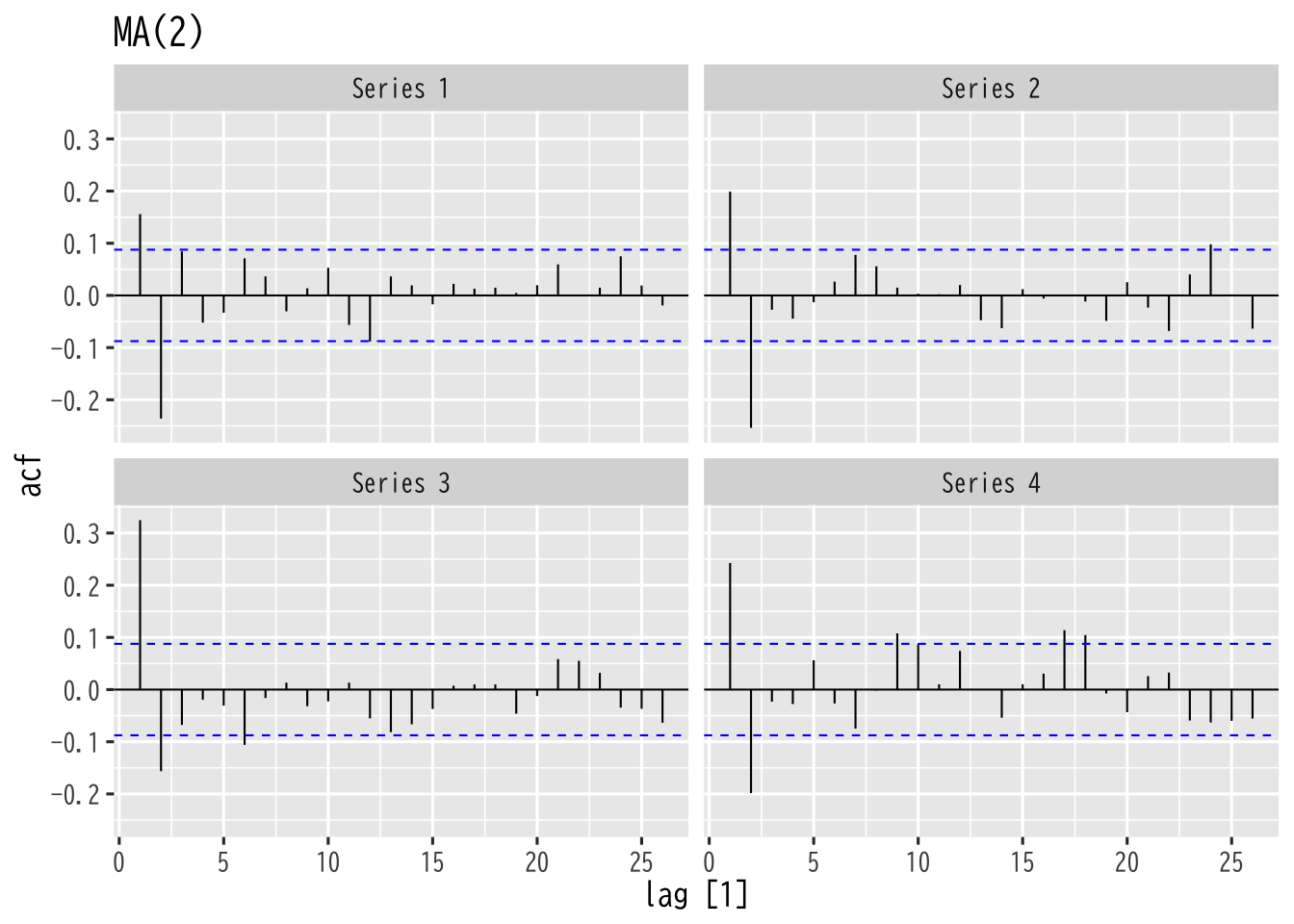
Figure 4: MA過程の自己相関

13_arma.png

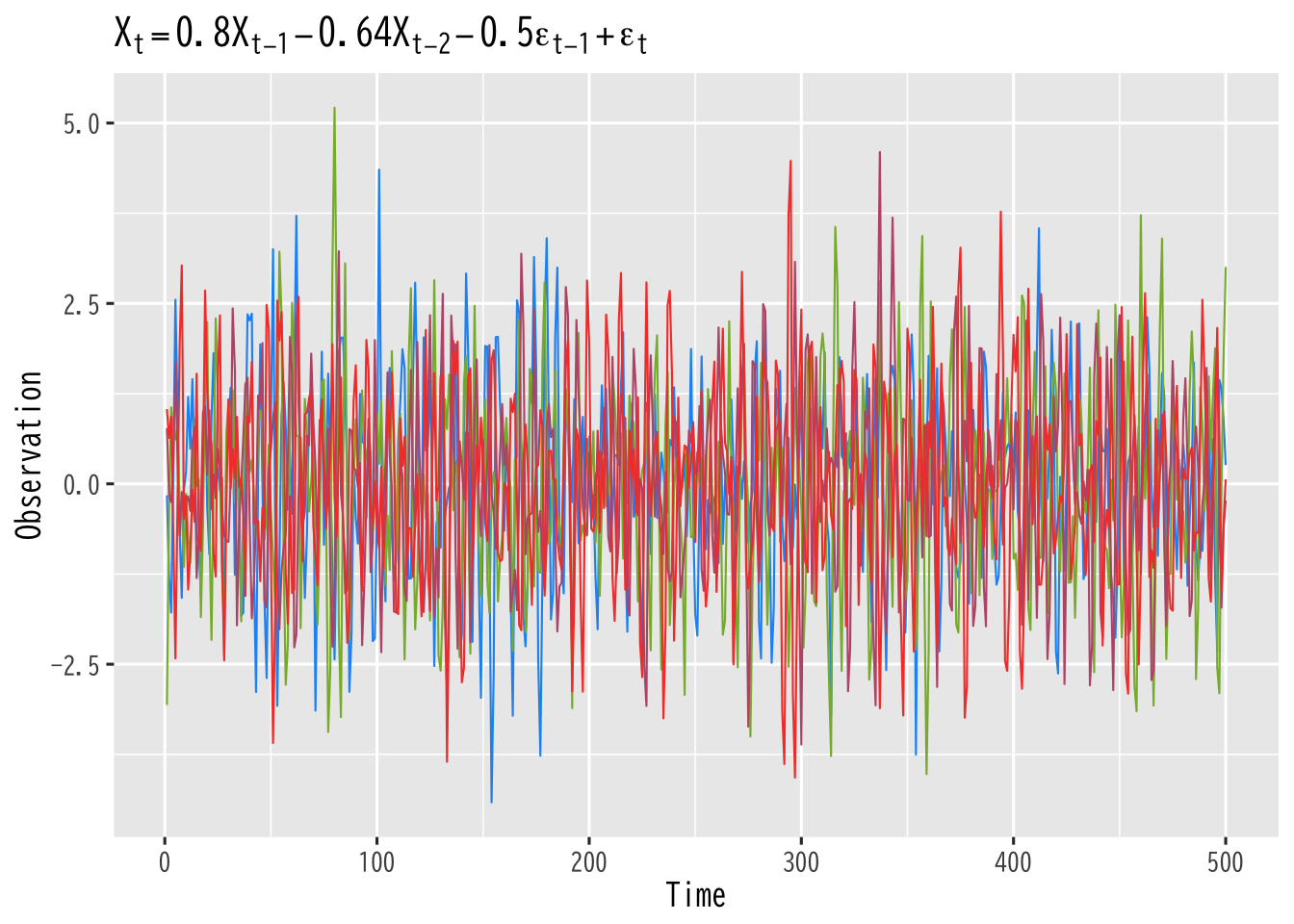
Figure 5: 同じモデルに従うARMA過程の例

13_armaacf.png

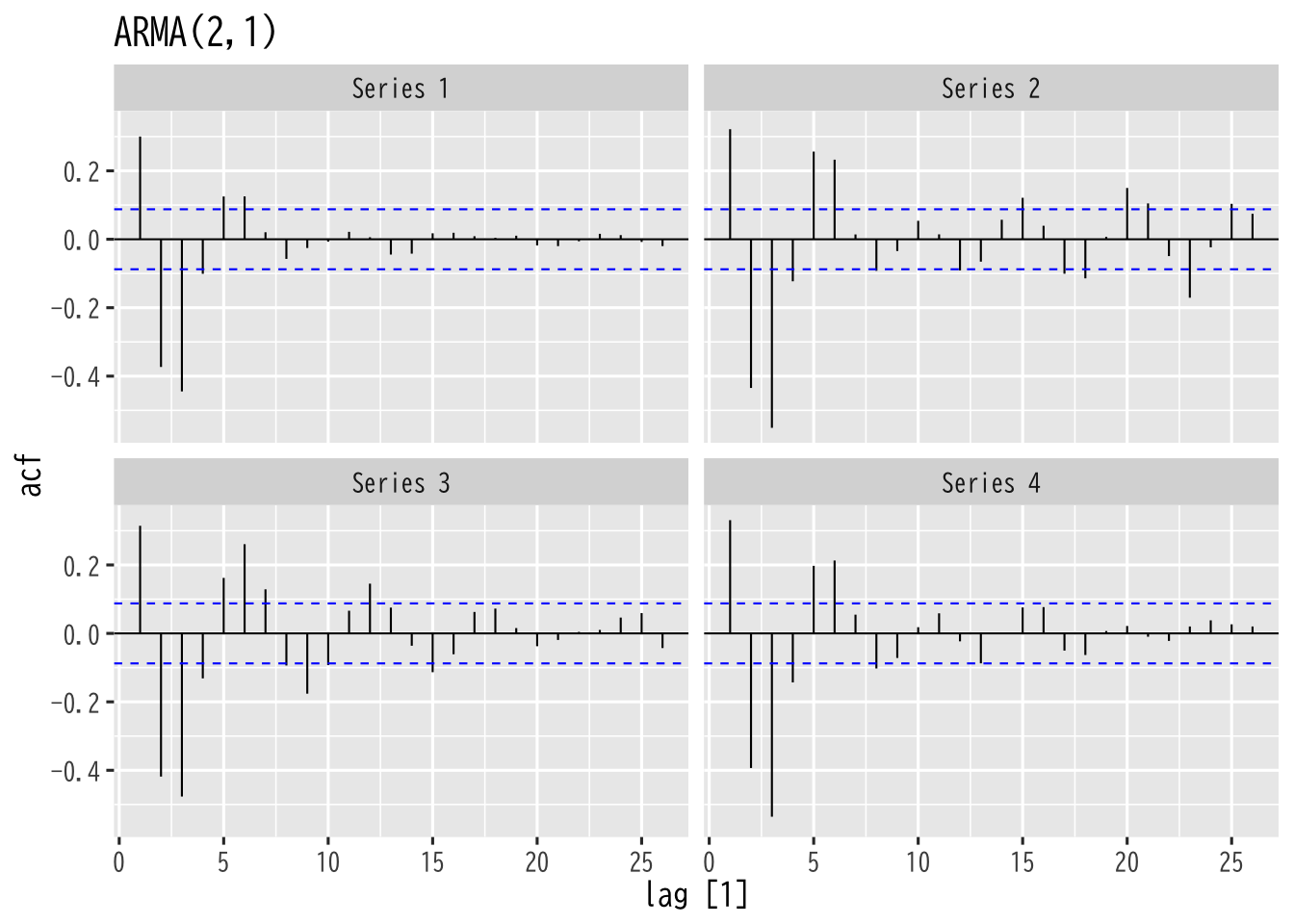
Figure 6: ARMA過程の自己相関

ARモデルの推定

自己共分散・自己相関

  • 平均\(0\)の弱定常な確率過程 : \(X_{t},\;t=1,\dotsc,T\)

    • \(X_{t}\) と \(X_{t+h}\) の共分散は時点\(t\)によらずラグ\(h\)のみで定まる

      自己共分散

      \begin{equation} \gamma(h) = \mathrm{Cov}(X_{t},X_{t+h}) = \mathbb{E}[X_{t}X_{t+h}] \end{equation}

    • \(X_{t}\)と\(X_{t+h}\)の相関も\(t\)によらずラグ\(h\)のみで定まる

      自己相関係数

      \begin{equation} \rho(h) =\mathrm{Cov}(X_{t},X_{t+h})/\mathrm{Var}(X_{t}) =\gamma(h)/\gamma(0) \end{equation}

自己共分散とARモデル

  • AR(p)モデル :

    \begin{equation} X_{t} = a_{1}X_{t-1}+a_{2}X_{t-2}+\dotsb+a_{p}X_{t-p}+\epsilon_{t} \end{equation}

  • 係数と自己共分散の関係

    \begin{align} \gamma(h) &= \mathbb{E}[X_{t}X_{t+h}]\\ &= \mathbb{E}[X_{t}(a_{1}X_{t+h-1}+\dotsb+a_{p}X_{t+h-p}+\epsilon_{t+h})]\\ &= a_{1}\mathbb{E}[X_{t}X_{t+h-1}] +\dotsb +a_{p}\mathbb{E}[X_{t}X_{t+h-p}] +\mathbb{E}[X_{t}\epsilon_{t+h}]\\ &= a_{1}\gamma(h-1) +\dotsb+ a_{p}\gamma(h-p) \end{align}

Yule-Walker方程式

  • \(1\le h\le p\) を考えると以下の関係が成り立つ

    \begin{equation} \begin{pmatrix} \gamma(1)\\ \gamma(2)\\ \vdots\\ \gamma(p) \end{pmatrix} = \begin{pmatrix} \gamma(0)&\gamma(-1)&\dots&\gamma(-p+1)\\ \gamma(1)&\gamma(0)&\dots&\gamma(-p+2)\\ \vdots&\vdots&\ddots&\vdots\\ \gamma(p-1)&\gamma(p-2)&\dots&\gamma(0) \end{pmatrix} \begin{pmatrix} a_{1}\\ a_{2}\\ \vdots\\ a_{p} \end{pmatrix} \end{equation}
    • 行列は Toeplitz 行列と呼ばれる
    • 行列が正則ならばARの係数は一意に求まる

偏自己相関

  • AR(p)モデル

    \begin{equation} X_{t} = a_{1}X_{t-1}+a_{2}X_{t-2}+\dotsb+a_{p}X_{t-p}+\epsilon_{t} \end{equation}

    • ラグ\(p\)の 偏自己相関係数

      AR(p)モデルを仮定したときの\(a_{p}\)の推定値 (Yule-Walker方程式の解)

    • ラグ\(p\)の特別な 自己相関係数

      \(a_{1}=a_{2}=\dotsb=a_{p-1}=0\)のときの\(\rho(p)\) (特殊なモデルにおける解釈)

      \begin{equation} \mathbb{E}[X_{t}X_{t+p}]=a_{p}\mathbb{E}[X_{t}X_{t}] \;\Rightarrow\; \gamma(p)=a_{p}\gamma(0) \;\Rightarrow\; \rho(p)=a_{p} \end{equation}

13_arpacf.png

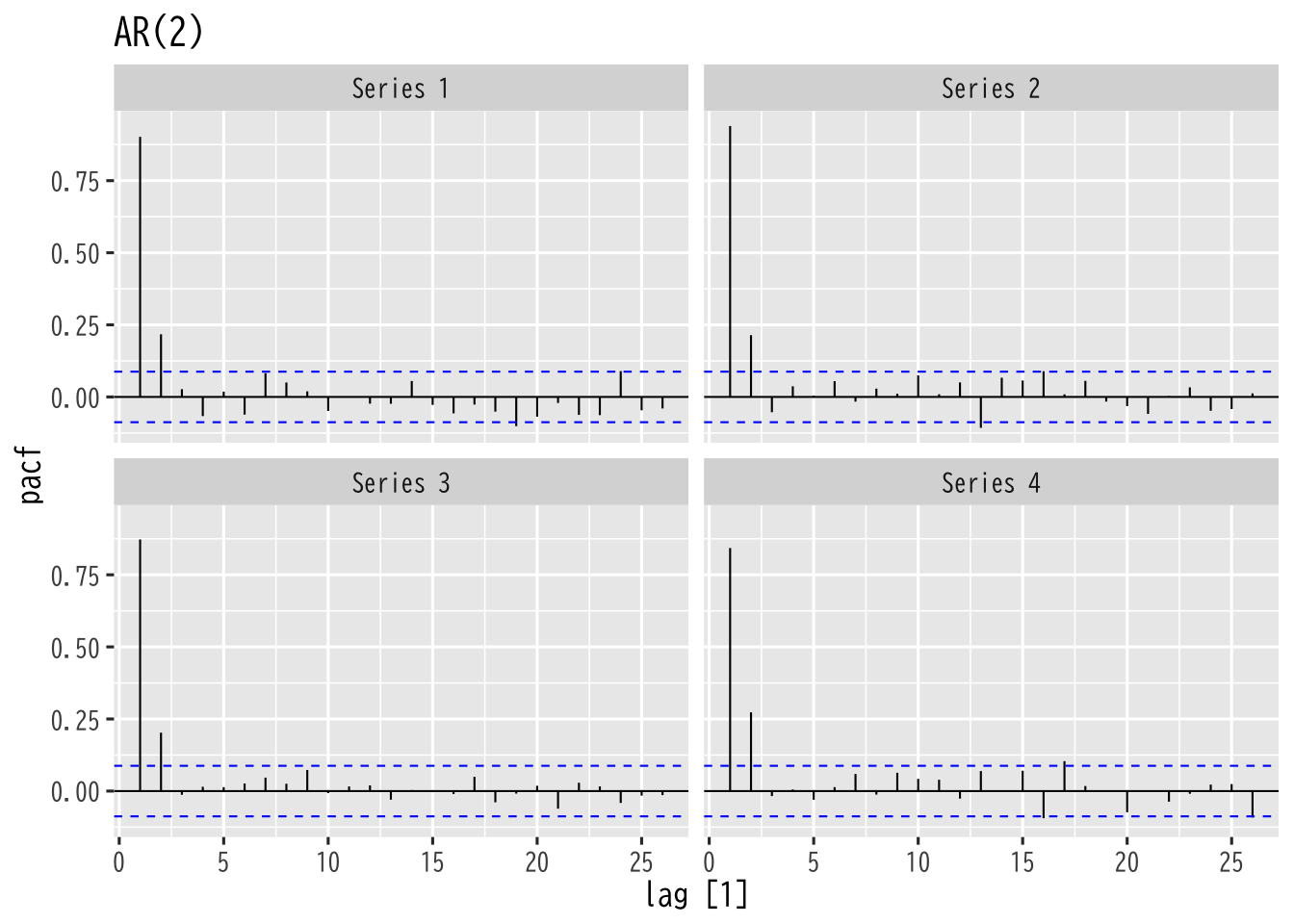
Figure 7: AR過程の偏自己相関

13_mapacf.png

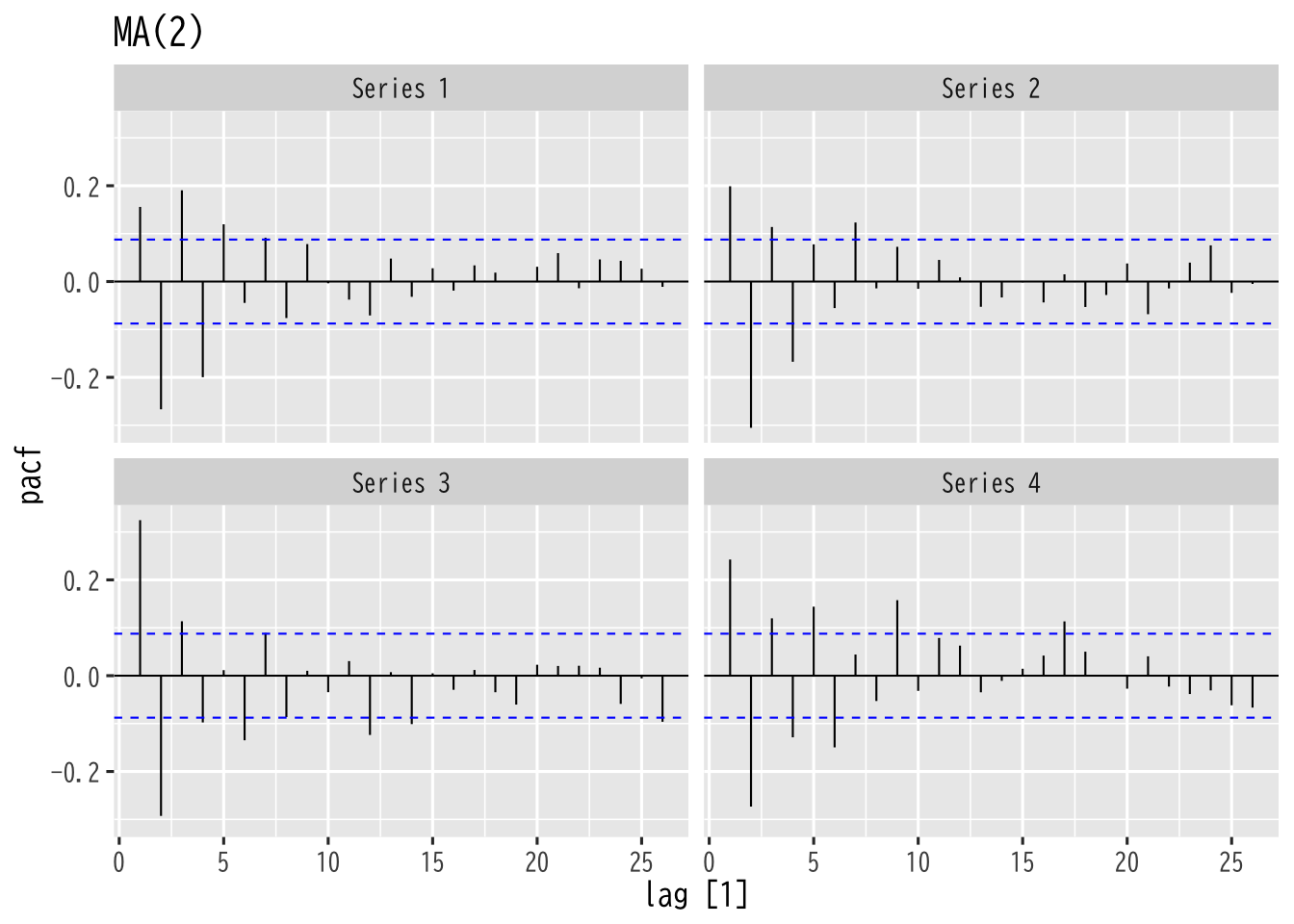
Figure 8: MA過程の偏自己相関

13_armapacf.png

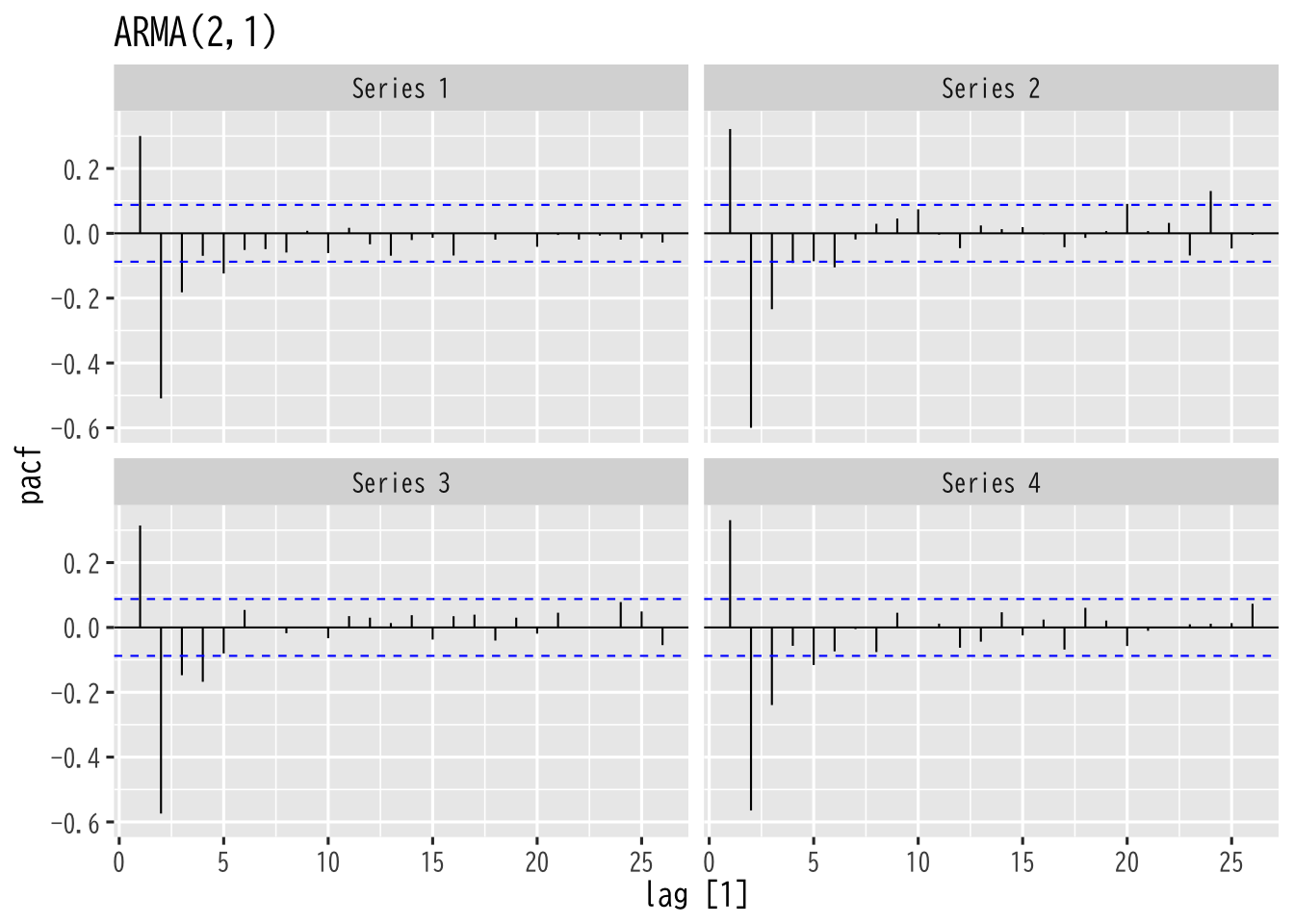
Figure 9: ARMA過程の偏自己相関

モデルの推定に関する補足

  • ARMAモデルの推定方法は主に以下の3つ
    • Yule-Walker方程式 (AR過程)
    • 最小二乗
      • 予測誤差の平方和の最小化
      • 回帰と同じだが，従属系列のため多重共線性に注意
    • 最尤推定
      • WNの分布を仮定して同時尤度関数を設定
      • 非線形最適化を行う
  • 一般にモデルは近似なので，どの推定が良いかは問題による

非定常過程の変換

  • 定常過程とみなせるように変換して分析

    • 階差の利用

      \begin{equation} X_{t}=X_{t-1}+\epsilon_{t} \quad\Rightarrow\quad Y_{t}=X_{t}-X_{t-1}=\epsilon_{t} \end{equation}
      • ランダムウォーク : 階差をとるとホワイトノイズ(定常過程)
      • ARIMA過程 : 階差をとるとARMA過程になる確率過程

    • 対数変換の利用

      \begin{equation} X_{t}=(1+\epsilon_{t})X_{t-1} \quad\Rightarrow\quad Y_{t}=\log(X_{t})-\log(X_{t-1}) =\log(1+\epsilon_{t}) \simeq\epsilon_{t} \end{equation}
      • 対数変換と階差で微小な比率の変動を抽出

演習

問題

  • 以下で定義されるMA(1)について問に答えなさい

    \begin{equation} X_{t} = b_{1}\epsilon_{t-1}+\epsilon_{t}, \quad \epsilon_{t} \sim \mathrm{WN}(0,\sigma^2) \end{equation}
    • ラグ2までの自己共分散係数を求めなさい
    • 自己相関係数とパラメタ\(b_{1}\)が満すべき方程式を求めなさい

解答例

  • 平均0であることに注意して定義通り計算する

    \begin{align} \gamma(0) &= \mathbb{E}[X_{t}X_{t}] = \mathbb{E}[(b_{1}\epsilon_{t-1}+\epsilon_{t})^{2}]\\ &= b_{1}^{2}\mathbb{E}[\epsilon_{t-1}^{2}] +2b_{1}\mathbb{E}[\epsilon_{t-1}\epsilon_{t}] +\mathbb{E}[\epsilon_{t}^{2}]\\ &= (b_{1}^{2}+1)\sigma^{2}\\ \gamma(1) &= \mathbb{E}[X_{t}X_{t+1}] = \mathbb{E}[(b_{1}\epsilon_{t-1}+\epsilon_{t})(b_{1}\epsilon_{t}+\epsilon_{t+1})]\\ &= b_{1}^{2}\mathbb{E}[\epsilon_{t-1}\epsilon_{t}] +b_{1}\mathbb{E}[\epsilon_{t-1}\epsilon_{t+1}] +b_{1}\mathbb{E}[\epsilon_{t}\epsilon_{t}] +\mathbb{E}[\epsilon_{t}\epsilon_{t+1}]\\ &= b_{1}\sigma^{2}\\ \gamma(2) &= \mathbb{E}[X_{t}X_{t+2}] = \mathbb{E}[(b_{1}\epsilon_{t-1}+\epsilon_{t})(b_{1}\epsilon_{t+1}+\epsilon_{t+2})]\\ &= b_{1}^{2}\mathbb{E}[\epsilon_{t-1}\epsilon_{t+1}] +b_{1}\mathbb{E}[\epsilon_{t-1}\epsilon_{t+2}] +b_{1}\mathbb{E}[\epsilon_{t}\epsilon_{t+1}] +\mathbb{E}[\epsilon_{t}\epsilon_{t+2}]\\ &= 0 \end{align}

  • ラグ3以降も自己共分散は0となることに注意する

    \begin{align} \gamma(0) &= (b_{1}^{2}+1)\sigma^{2}\\ \gamma(1) &= b_{1}\sigma^{2} \end{align}

    \(\sigma^{2}\)を消去して以下が得られる

    \begin{equation} \gamma(1)/\gamma(0) =\frac{b_{1}}{b_{1}^{2}+1} =\rho(1) \end{equation}
    \begin{equation} \rho(1)b_{1}^{2}-b_{1}+\rho(1)=0 \end{equation}

    \(\rho(1)\)の値によっては解が求められない場合もある

モデルによる予測

ARMAモデルによる予測

  • 推定したモデルを用いて\(n\)期先を予測
    • ARモデル : 観測時点までの観測値を用いて回帰
    • MAモデル : 観測時点までのホワイトノイズで回帰
    • ARMAモデル : 上記の複合
  • いずれも \(n\)が大きいと不確定性が増大
  • 階差による変換は累積(階差の逆変換)により推定

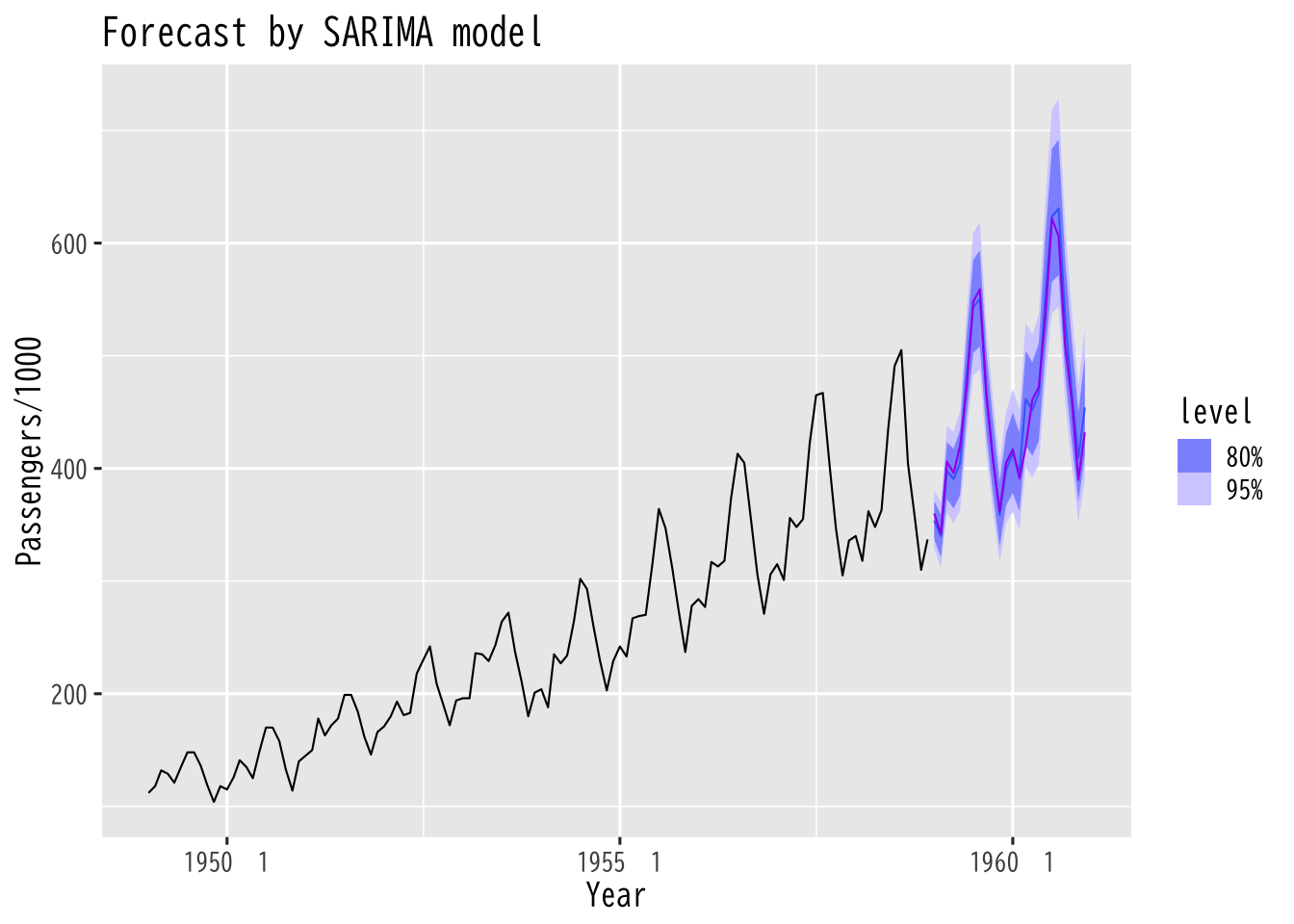
13_ap_arima.png

Figure 10: ARIMAモデル(階差ありARMA)による予測

分解モデルによる予測

  • トレンド成分+季節成分+ランダム成分への分解

    \begin{equation} X_{t}=T_{t}+S_{t}+R_{t} \end{equation}

    あるいは

    \begin{equation} X_{t}=T_{t}\times S_{t}\times R_{t}\qquad (\log X_{t}=\log T_{t} + \log S_{t} + \log R_{t}) \end{equation}
    • トレンド成分 : 時間の関数やランダムウォークなどを想定
    • 季節成分 : 周期的な関数を想定
    • ランダム成分 : ARMAモデルなどを想定
  • 分解の考え方
    • ランダム成分 : 適切な幅の移動平均が0
    • 季節成分 : 1周期の平均が0

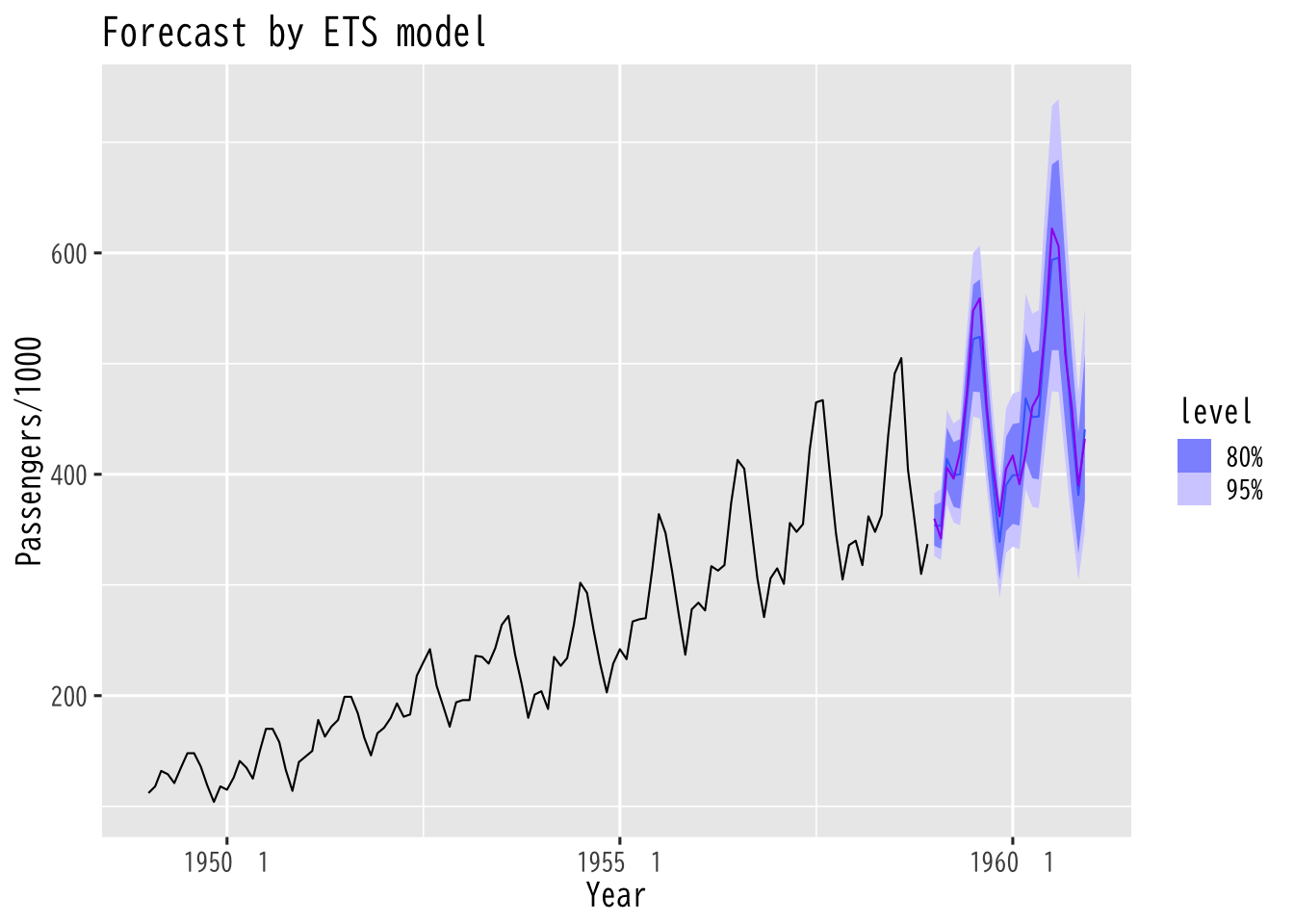
13_ap_ets.png

Figure 11: ETSモデル(expornential smoothing)による予測

解析事例

COVID-19 の感染者数の分析

  • 厚生労働省の COVID-19 のデータ
    • 陽性者数 (新規・累積)
    • 重症者数 (推移・性別・年齢別)
    • 死者数 (推移・性別・年齢別・累積)
    • 入院治療等を要する者等推移
    • 集団感染等発生状況
  • 以下の解析で用いるデータ

感染者数の推移

13_patients.png

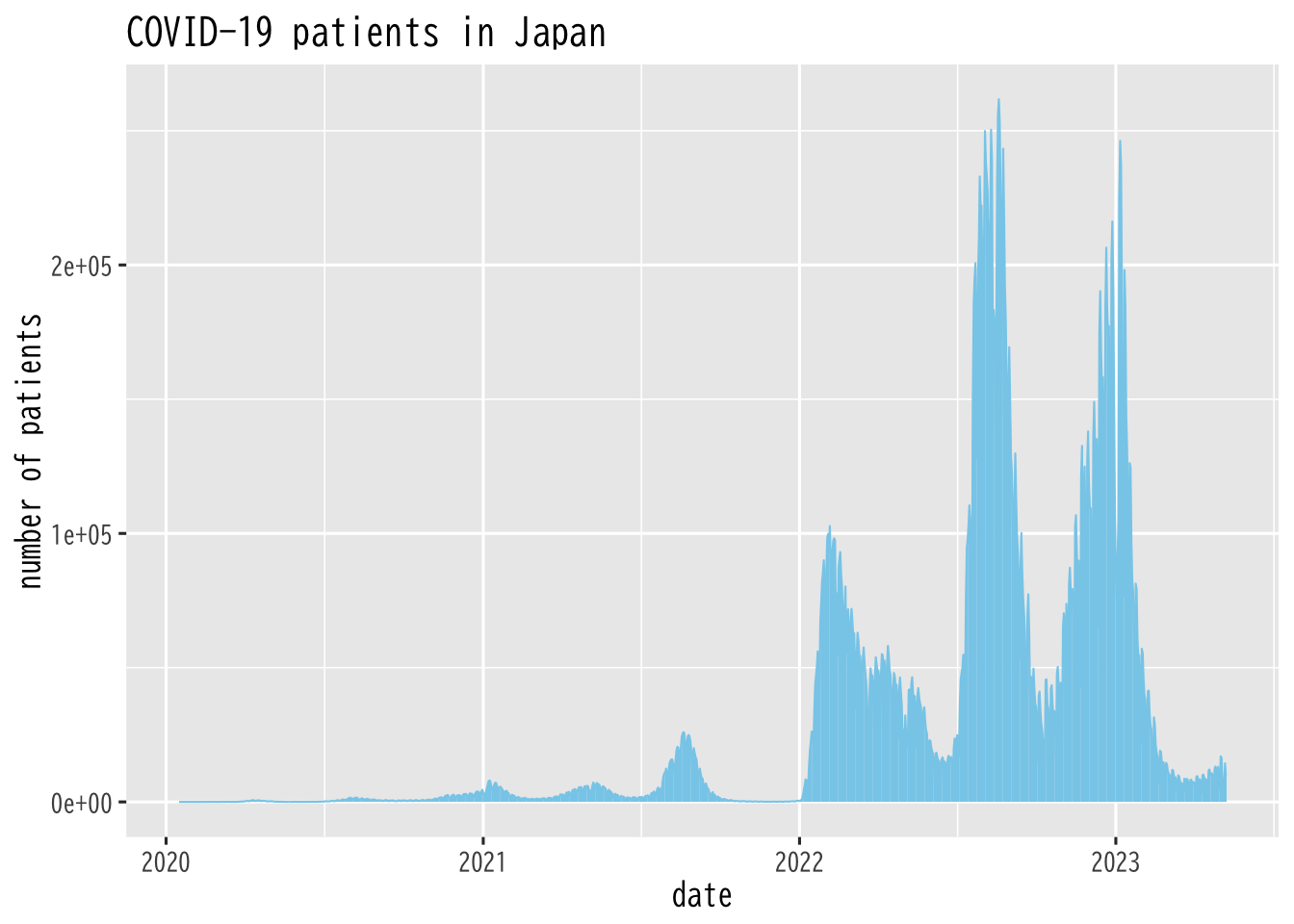
Figure 12: 全国の感染者数

第3波における感染者数の推移

13_3wave_patients.png

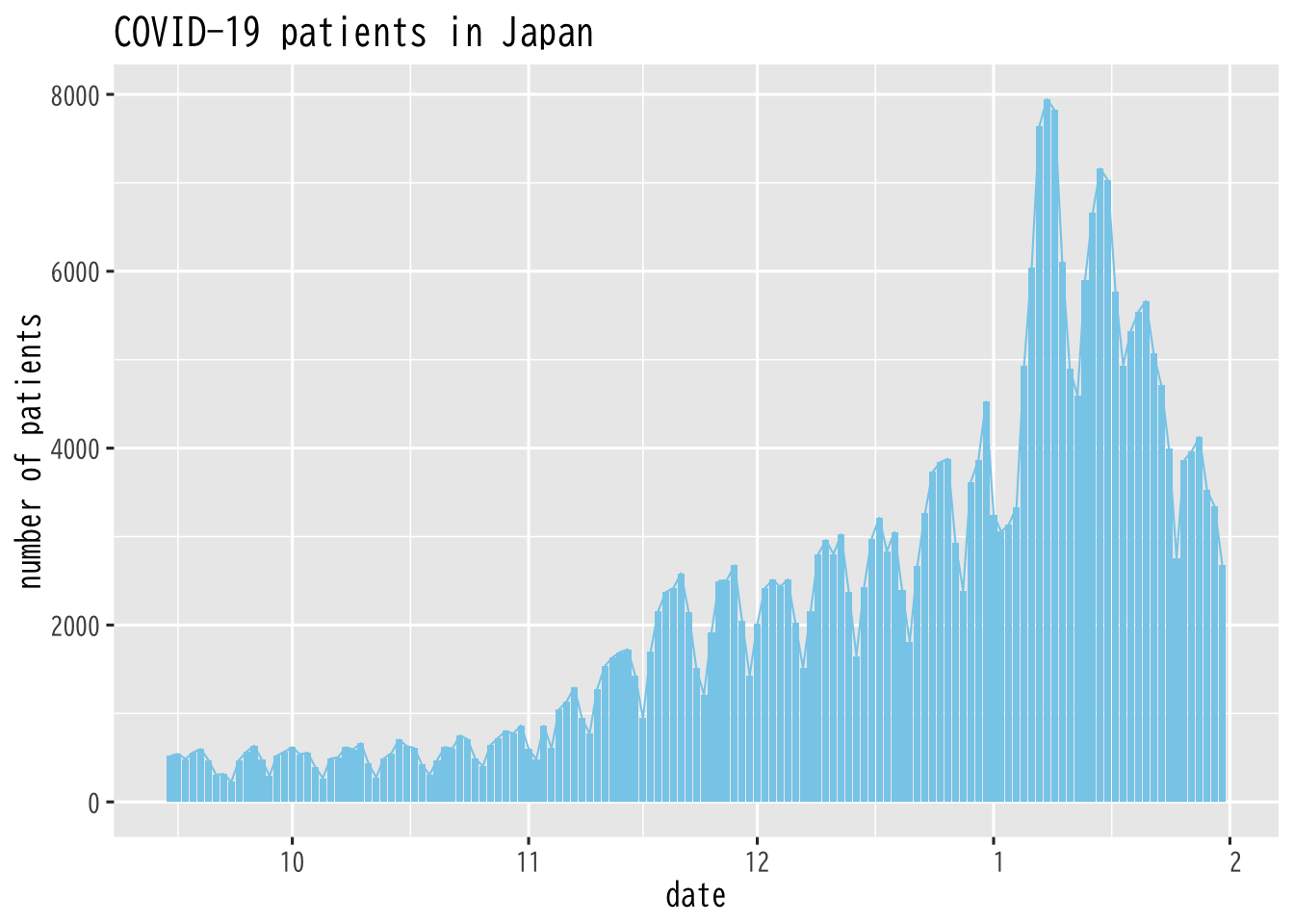
Figure 13: 第3波の感染者数

基礎分析 (分析対象 : 2020/9/15-11/30)

13_3wave.png

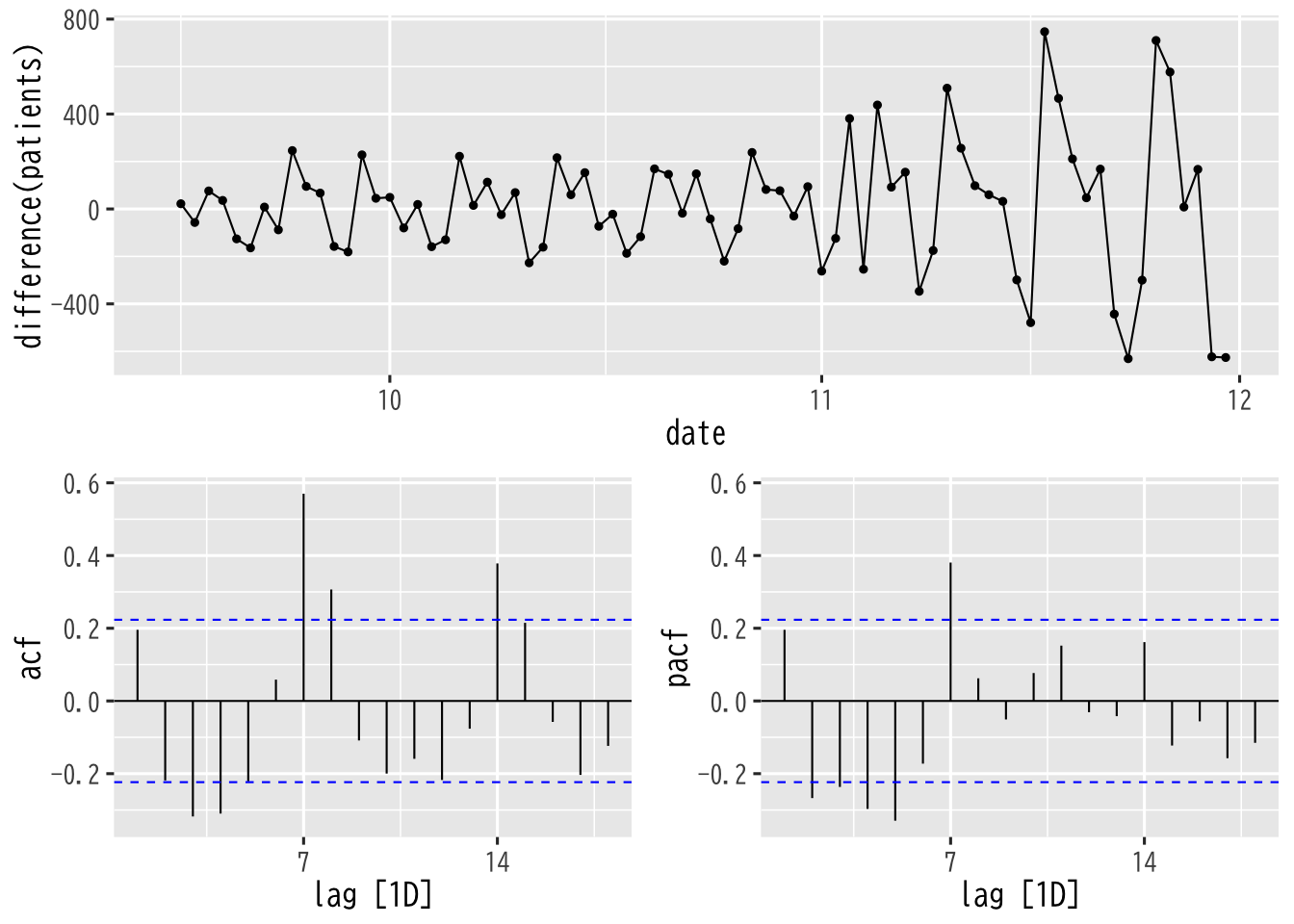
Figure 14: 時系列 (階差)

13_3wave_log.png

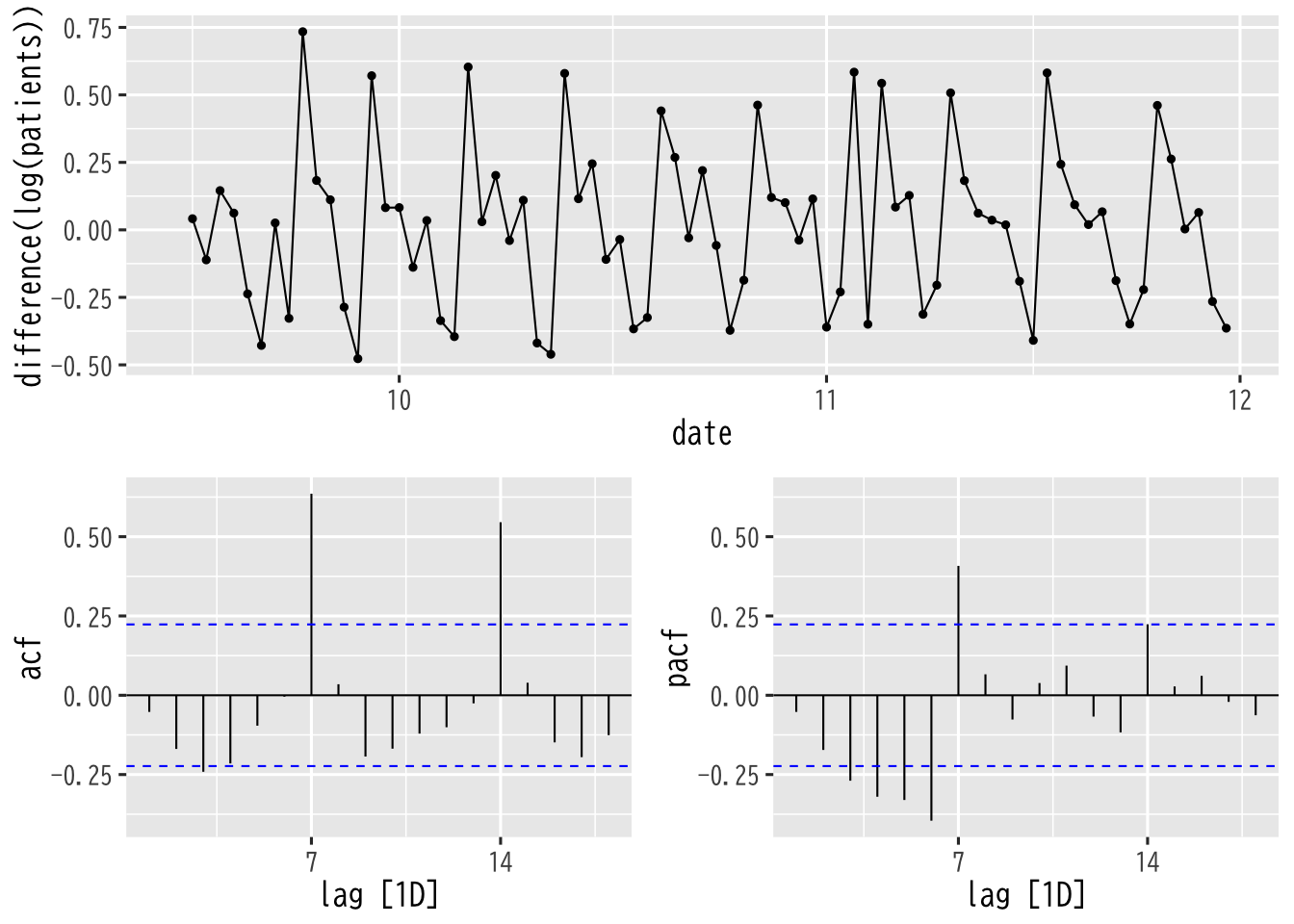
Figure 15: 時系列 (対数変換+階差)

13_3wave_log7.png

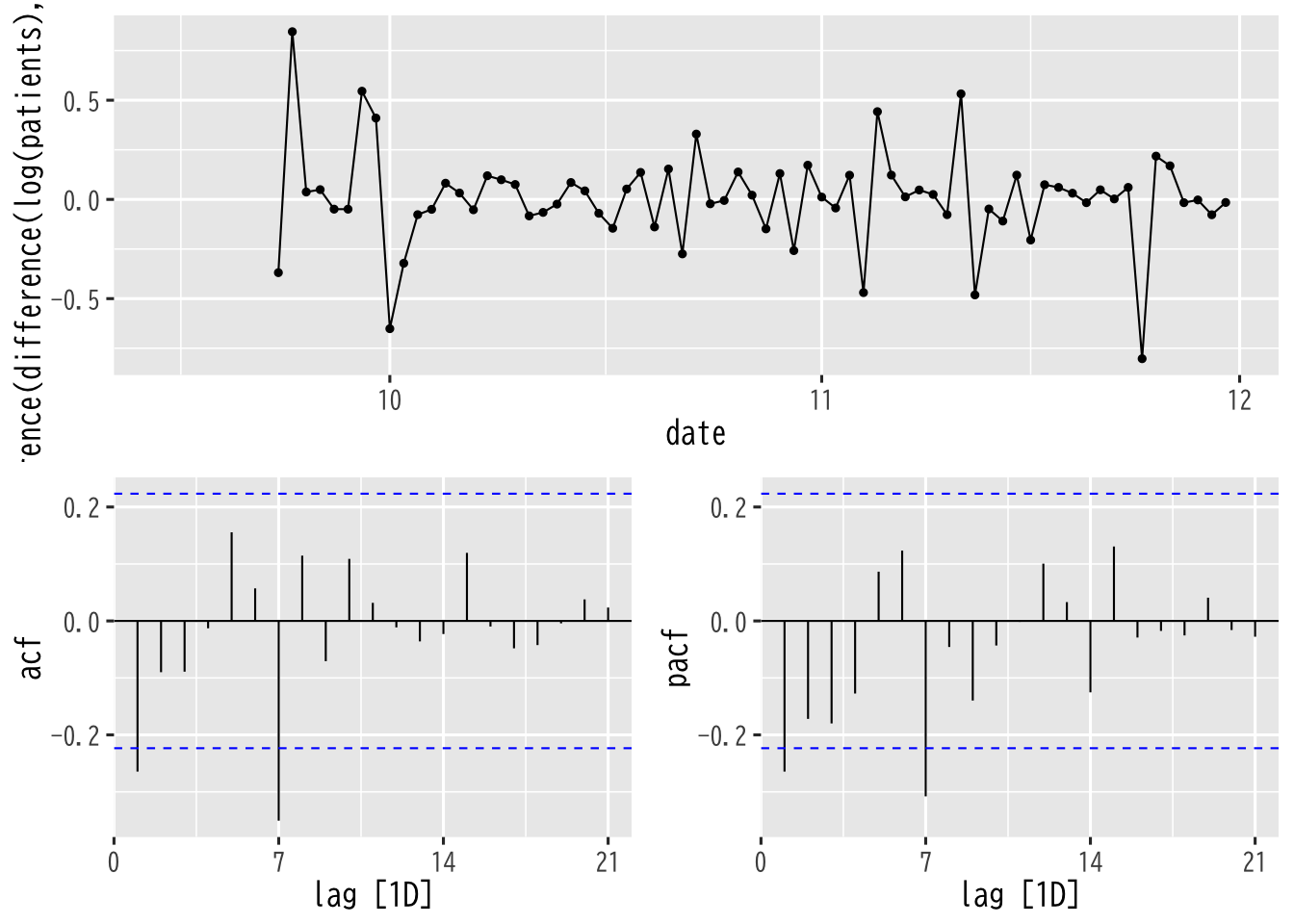
Figure 16: 時系列 (対数変換+階差+7日階差)

ARIMA モデルによる推定

  • 推定された ARIMA モデル
Series: patients 
Model: ARIMA(1,1,1)(2,0,0)[7] 
Transformation: log(patients) 

Coefficients:
         ar1      ma1    sar1    sar2
      0.4493  -0.8309  0.3709  0.4232
s.e.  0.1635   0.0981  0.1212  0.1353

sigma^2 estimated as 0.03811:  log likelihood=15.04
AIC=-20.07   AICc=-19.21   BIC=-8.42

13_3wave_arima_est.png

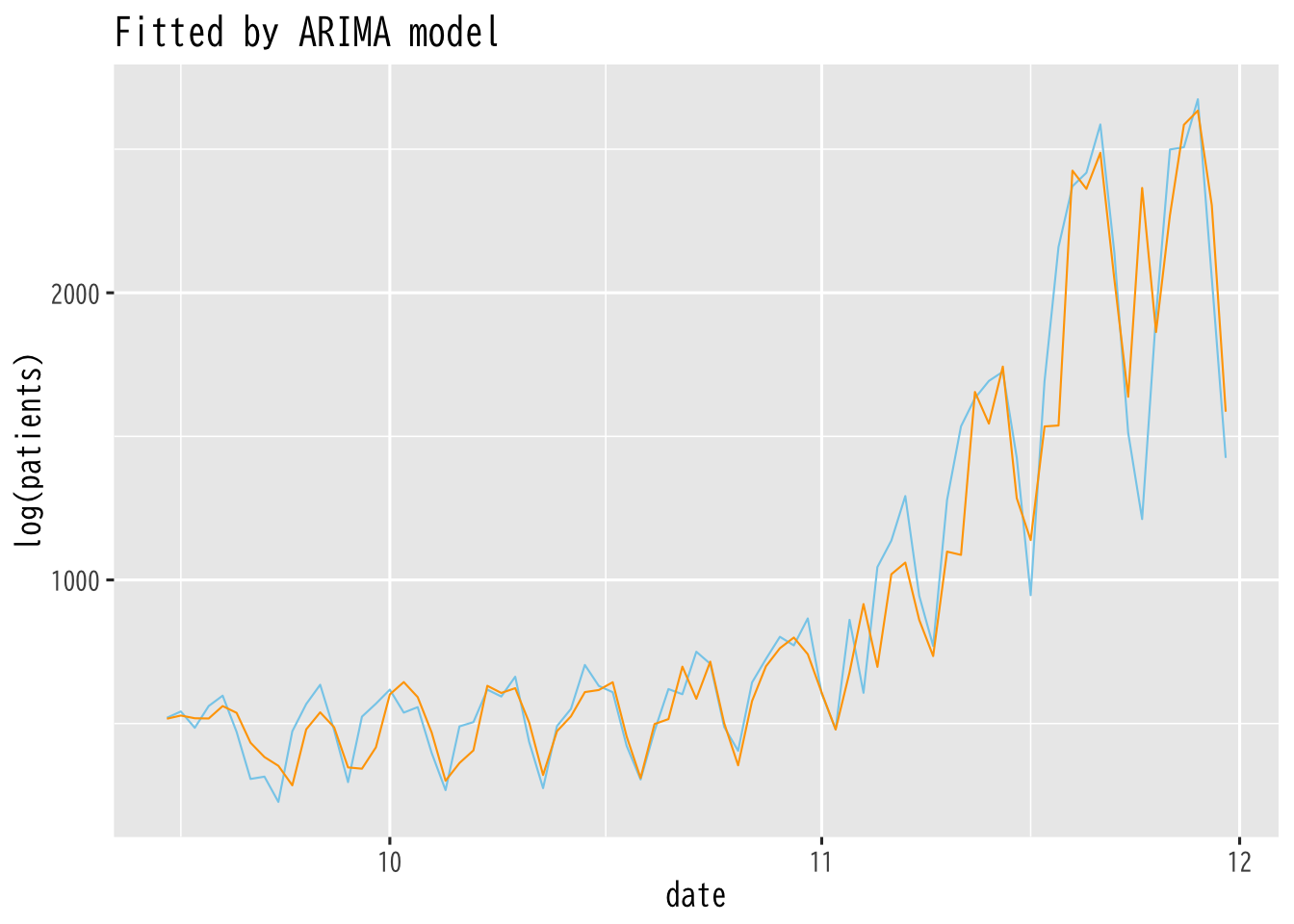
Figure 17: あてはめ値

13_3wave_arima_diag.png

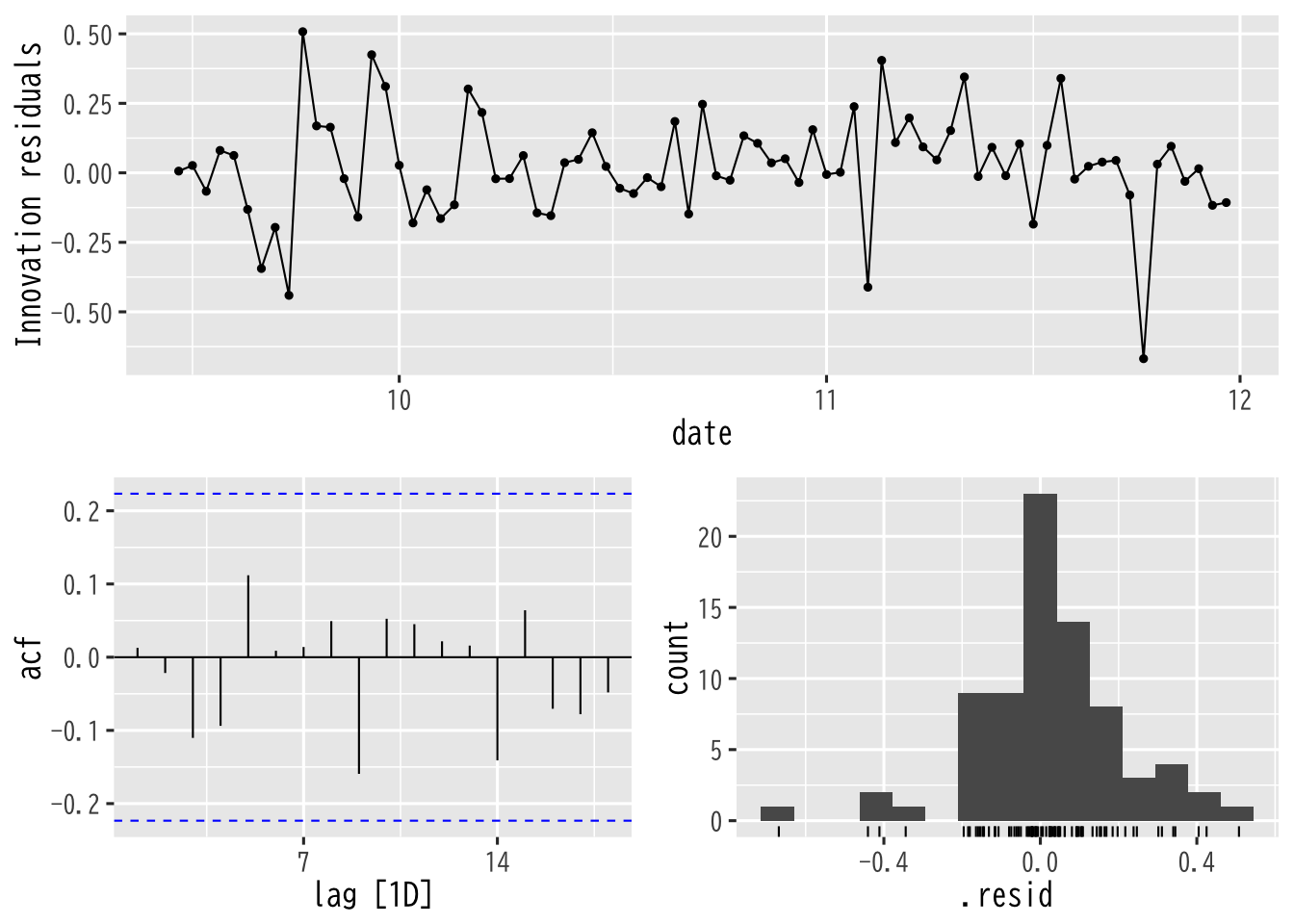
Figure 18: 診断プロット

13_3wave_arima_pred.png

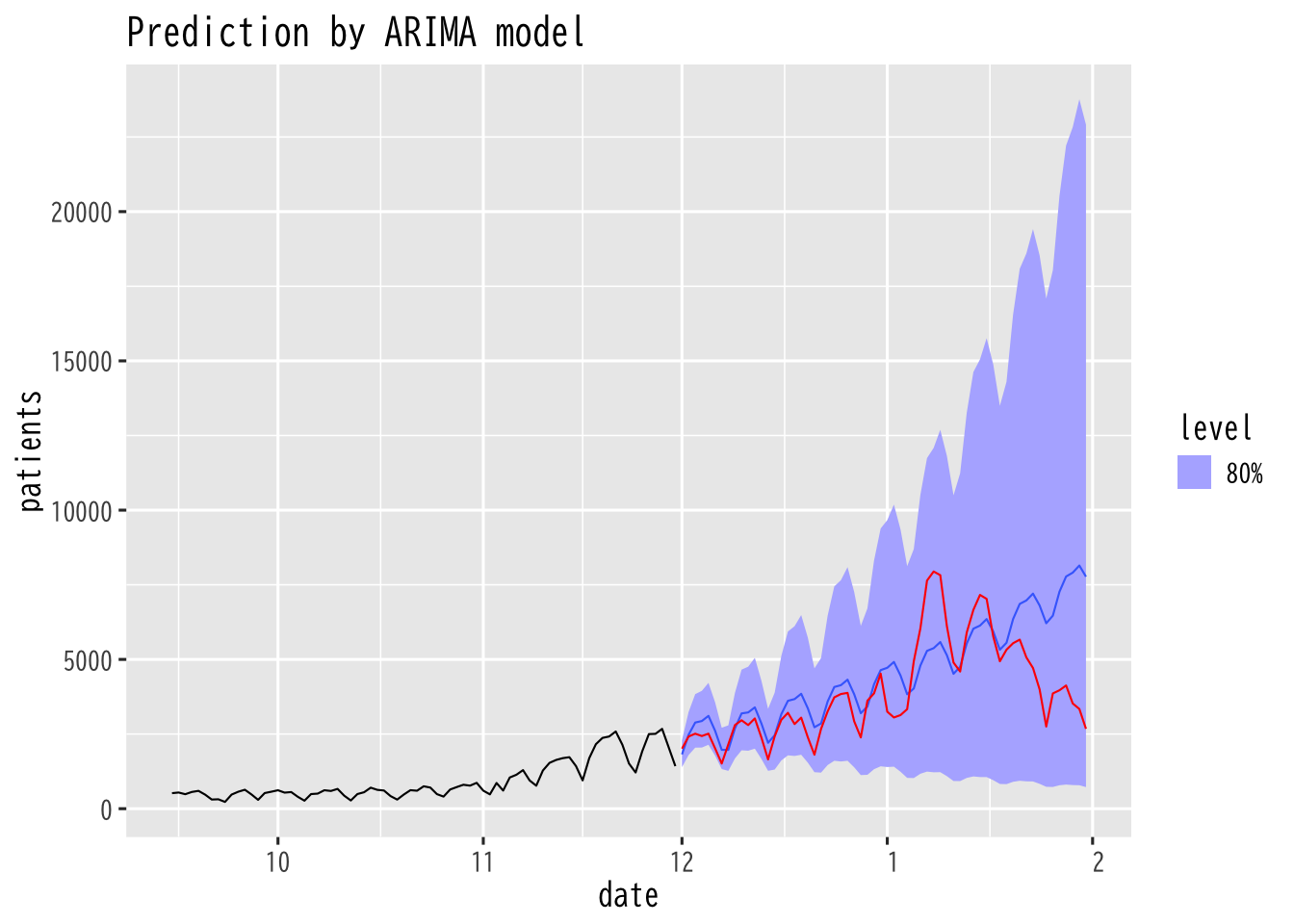
Figure 19: 予測値 (60日分，80%信頼区間)

まとめ

  • 感染者数の推移は非定常なデータ

  • 構造が時不変と考えられる区間を捉えれば

    • 時系列の適切な変換 (指数的な増大のため対数変換)
    • 基本的なARMAモデル (階差系列にARMAモデルを適用)

    の組み合わせである程度の分析は可能