時系列解析
時系列の基本モデル
(Press ? for help, n and p for next and previous slide)
村田 昇
講義の内容
- 第1回 : 時系列の基本モデル
- 第2回 : モデルの推定と予測
時系列解析の例
データの概要
- 米国の航空機旅客量の変遷データ
datasets::AirPassengers(Rに標準で収録)- 1949年から1960年までの月別の集計データ
出典
Box, G. E. P., Jenkins, G. M. and Reinsel, G. C. (1976) Time Series Analysis, Forecasting and Control. Third Edition. Holden-Day. Series G.
| year | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1949 | 112 | 118 | 132 | 129 | 121 | 135 | 148 | 148 | 136 | 119 | 104 | 118 |
| 1950 | 115 | 126 | 141 | 135 | 125 | 149 | 170 | 170 | 158 | 133 | 114 | 140 |
| 1951 | 145 | 150 | 178 | 163 | 172 | 178 | 199 | 199 | 184 | 162 | 146 | 166 |
| 1952 | 171 | 180 | 193 | 181 | 183 | 218 | 230 | 242 | 209 | 191 | 172 | 194 |
| 1953 | 196 | 196 | 236 | 235 | 229 | 243 | 264 | 272 | 237 | 211 | 180 | 201 |
| 1954 | 204 | 188 | 235 | 227 | 234 | 264 | 302 | 293 | 259 | 229 | 203 | 229 |
| 1955 | 242 | 233 | 267 | 269 | 270 | 315 | 364 | 347 | 312 | 274 | 237 | 278 |
| 1956 | 284 | 277 | 317 | 313 | 318 | 374 | 413 | 405 | 355 | 306 | 271 | 306 |
| 1957 | 315 | 301 | 356 | 348 | 355 | 422 | 465 | 467 | 404 | 347 | 305 | 336 |
| 1958 | 340 | 318 | 362 | 348 | 363 | 435 | 491 | 505 | 404 | 359 | 310 | 337 |
| 1959 | 360 | 342 | 406 | 396 | 420 | 472 | 548 | 559 | 463 | 407 | 362 | 405 |
| 1960 | 417 | 391 | 419 | 461 | 472 | 535 | 622 | 606 | 508 | 461 | 390 | 432 |
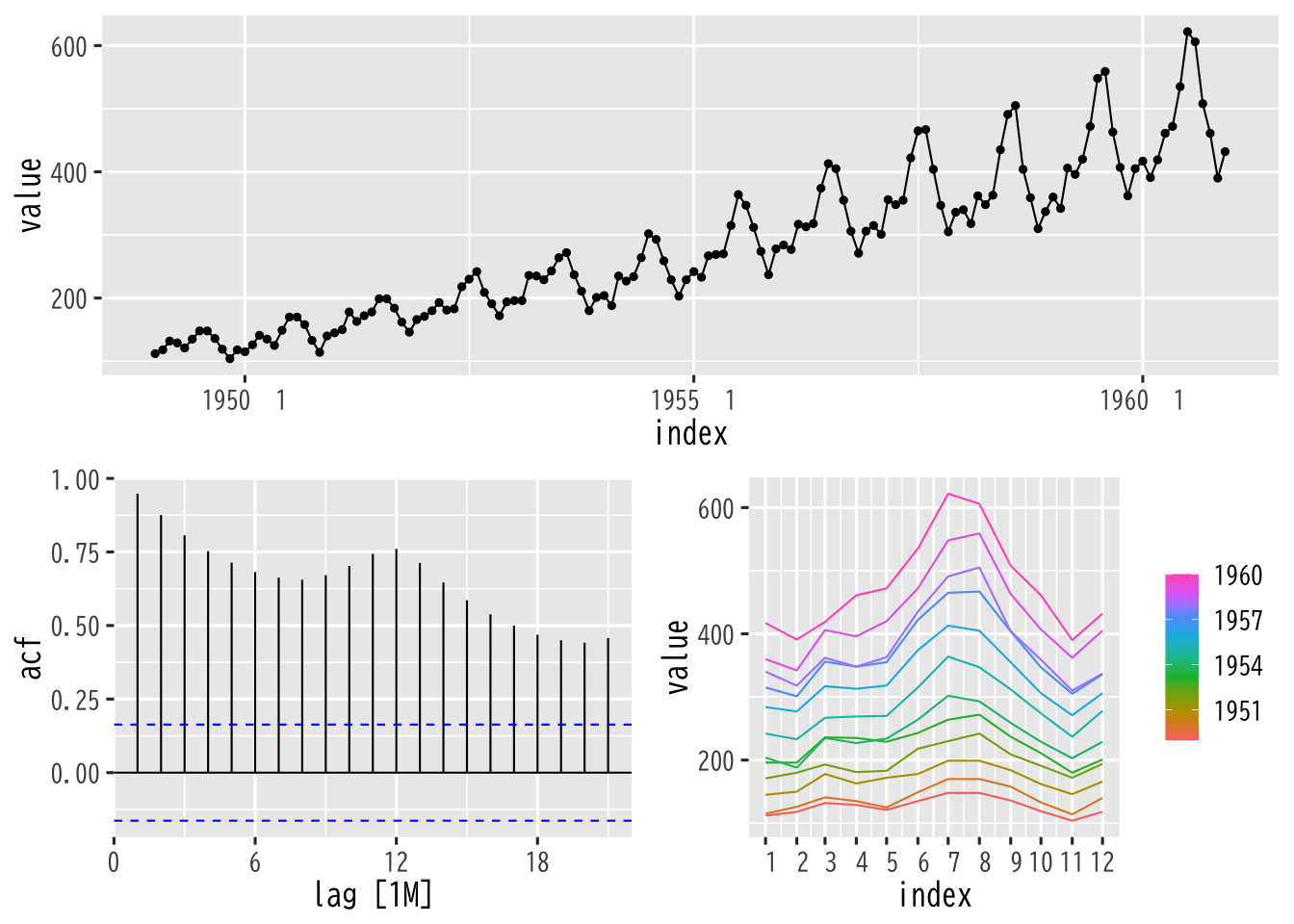
Figure 1: 航空機旅客量データ・自己相関・季節性の確認
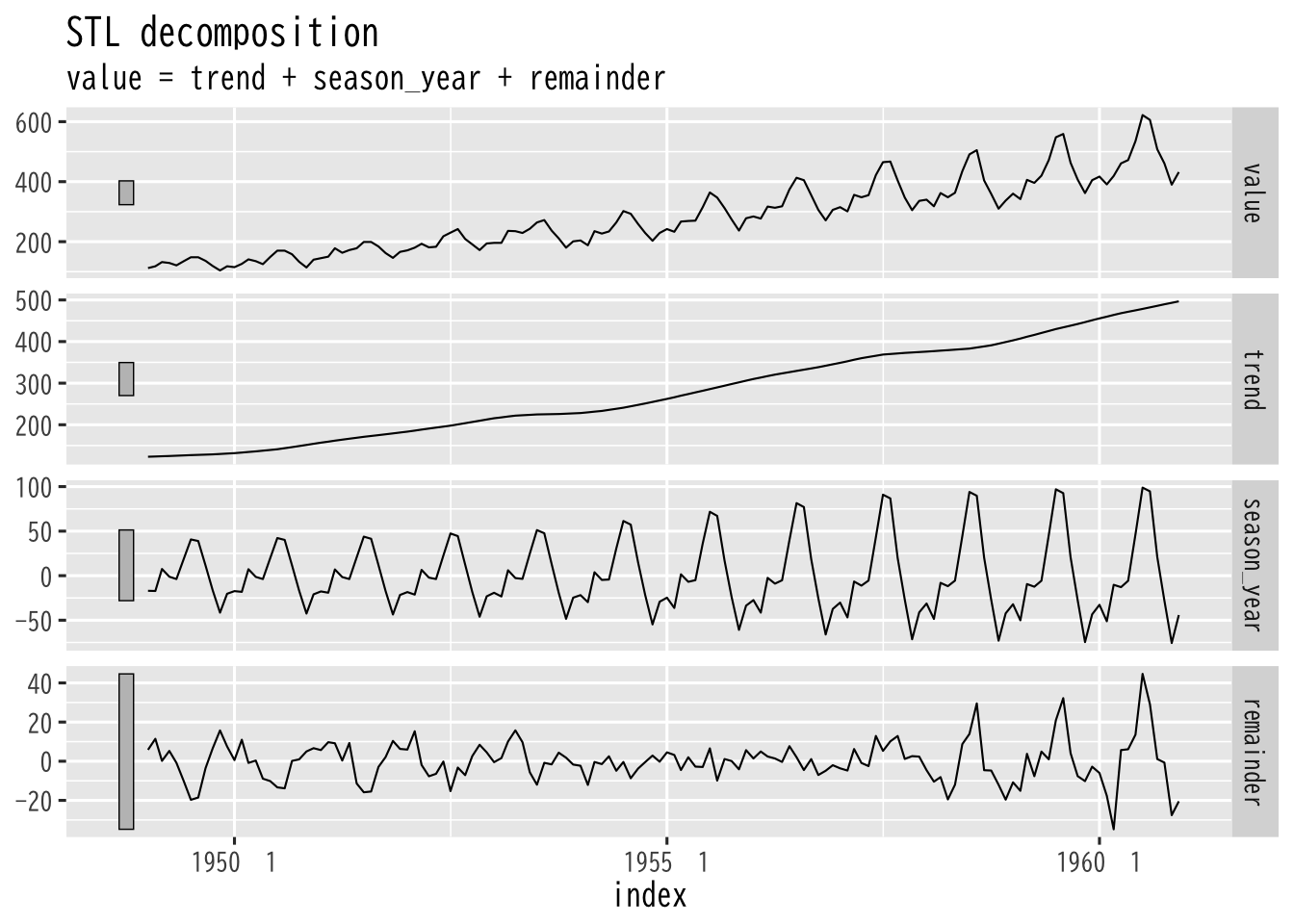
Figure 2: 時系列の分解による表現
データのモデル化
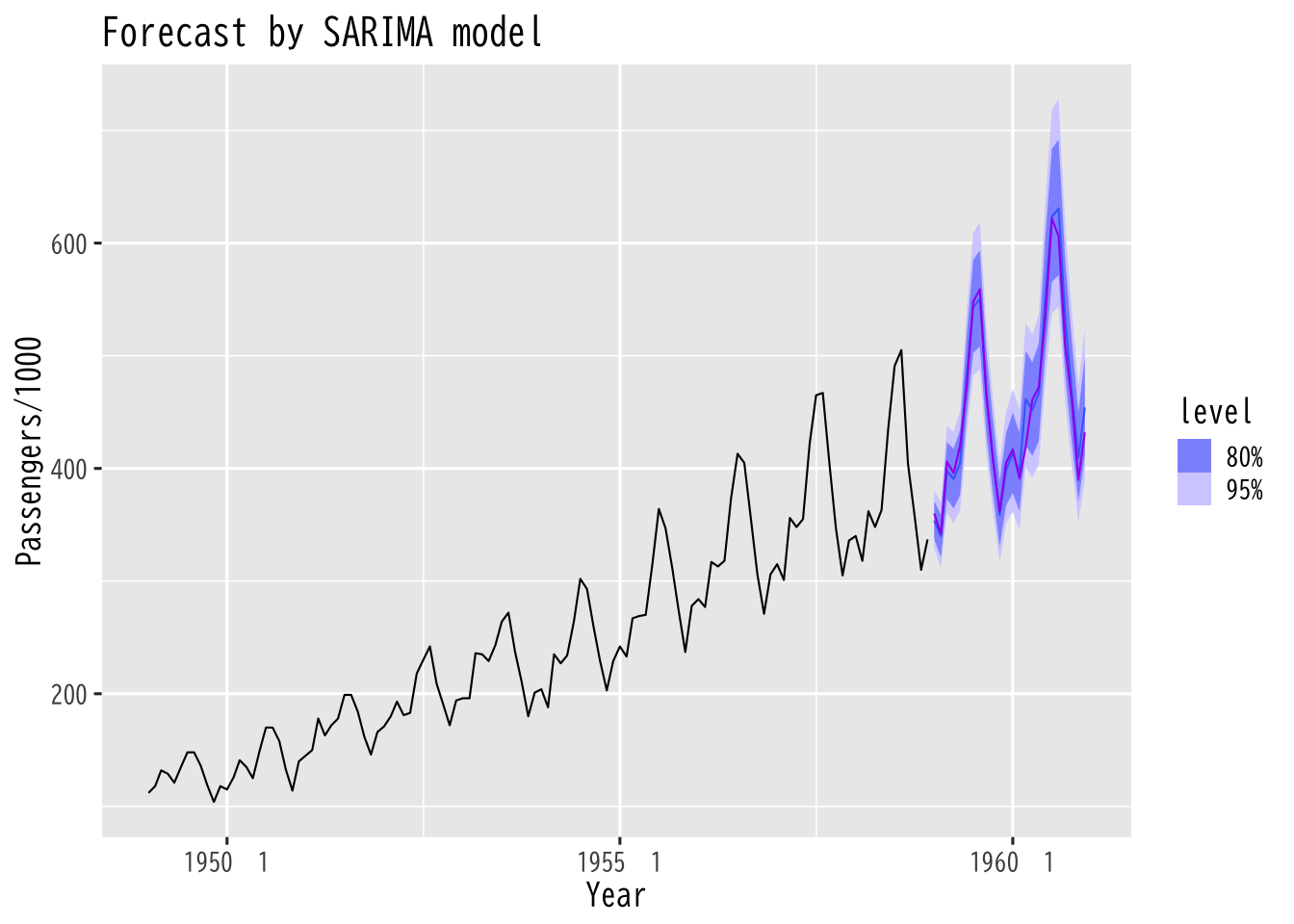
Figure 3: モデルの推定とあてはめ
モデルにもとづく予測
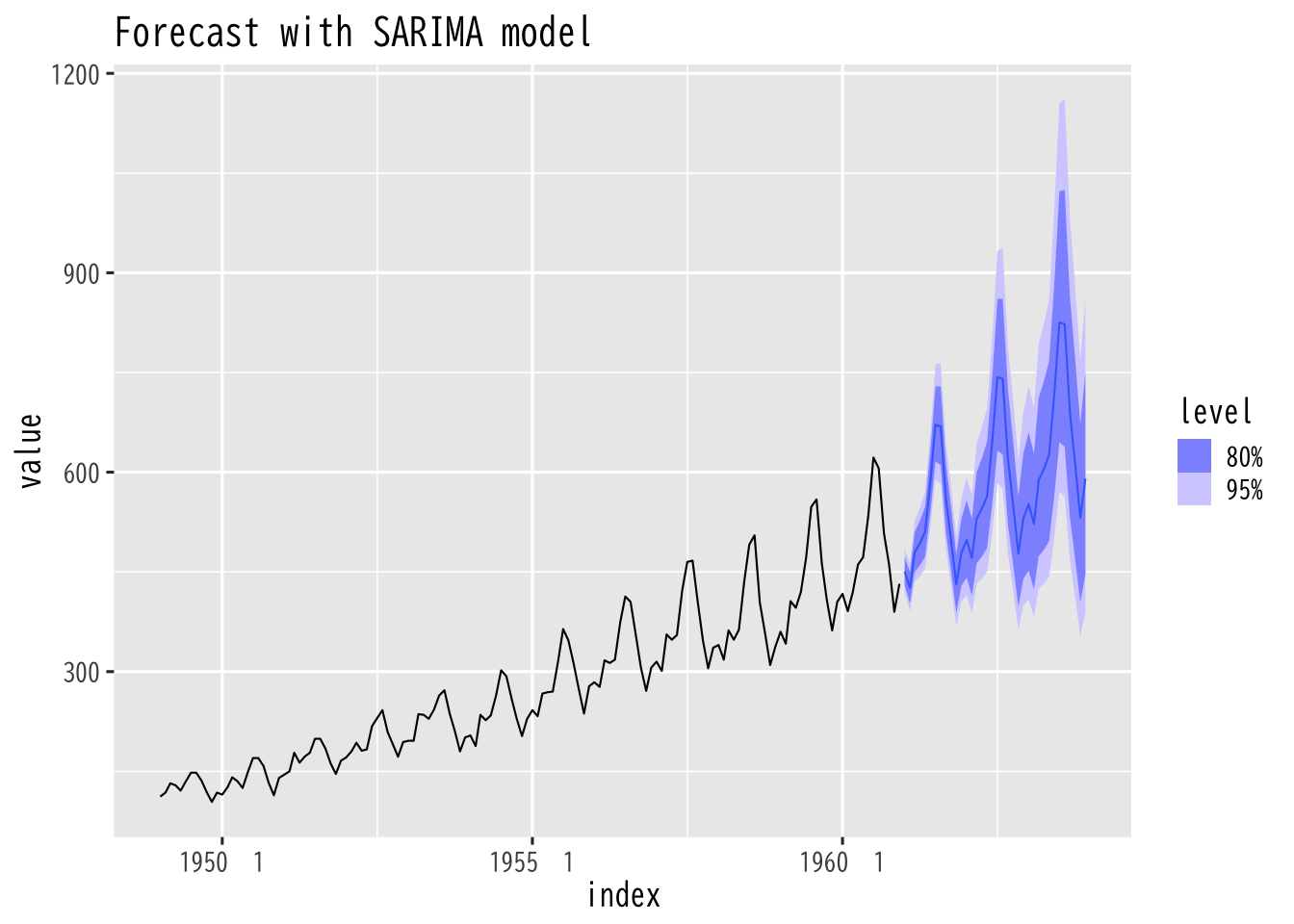
Figure 4: 航空機旅客量の予測
時系列解析の概要
時系列解析とは
- 時系列データ
- 時間軸に沿って観測されたデータ
- 観測の順序に意味がある
- 異なる時点間での観測データの従属関係が重要
- 独立性にもとづく解析は行えない
- そのままでは大数の法則や中心極限定理は使えない
- 時系列解析の目的
- 時系列データの特徴を効果的に記述すること
- 時系列モデルの推定と評価
時系列データ
統計学・確率論における表現 : 確率過程
時間を添え字として持つ確率変数列
\begin{equation} X_{t},\;t=1,2,\dotsc,T \quad(\text{あるいは}\;t=0,1,\dotsc,T) \end{equation}- 時系列解析で利用される代表的な確率過程
- ホワイトノイズ
- ランダムウォーク
- 自己回帰モデル (ARモデル)
- 移動平均モデル (MAモデル)
- 自己回帰移動平均モデル (ARMAモデル)
基本的なモデル
ホワイトノイズ
定義
平均 \(0\) 分散 \(\sigma^2\) である確率変数の 確率分布 \(P\) からの 独立かつ同分布な確率変数列
\begin{equation} X_{t} = \epsilon_{t}, \quad \epsilon_{t} \overset{i.i.d.}{\sim} P \end{equation}記号 \(\mathrm{WN}(0,\sigma^2)\) で表記することが多い
\begin{equation} X_{t} \sim \mathrm{WN}(0,\sigma^2) \end{equation}
- 独立であるため系列としての予測(点推定)は不可能
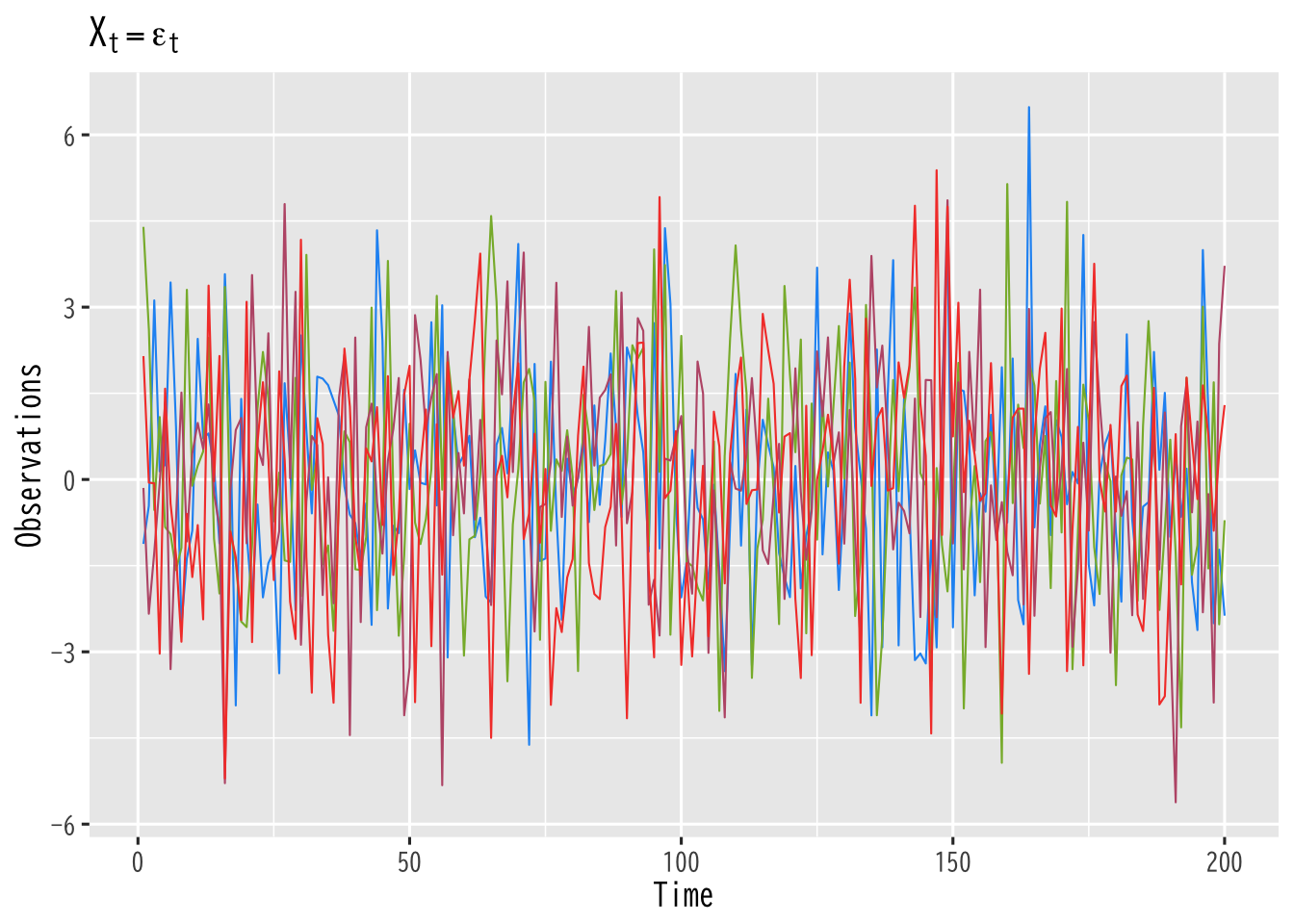
Figure 5: ホワイトノイズ (標準正規分布)
トレンドのあるホワイトノイズ
定義
\(\mu,\alpha\) を定数として 以下で定義される確率過程
\begin{equation} X_{t}=\mu+\alpha t+\epsilon_{t}, \quad \epsilon_{t} \sim \mathrm{WN}(0,\sigma^2) \end{equation}- トレンド \(\mu+\alpha t\) はより一般化されることもある
- \(t\) の1次式 (上記の基本的な場合)
- 高次の多項式
- 非線形関数(指数関数, 三角関数など)
- 平均 が時間とともに変動する時系列モデルの1つ
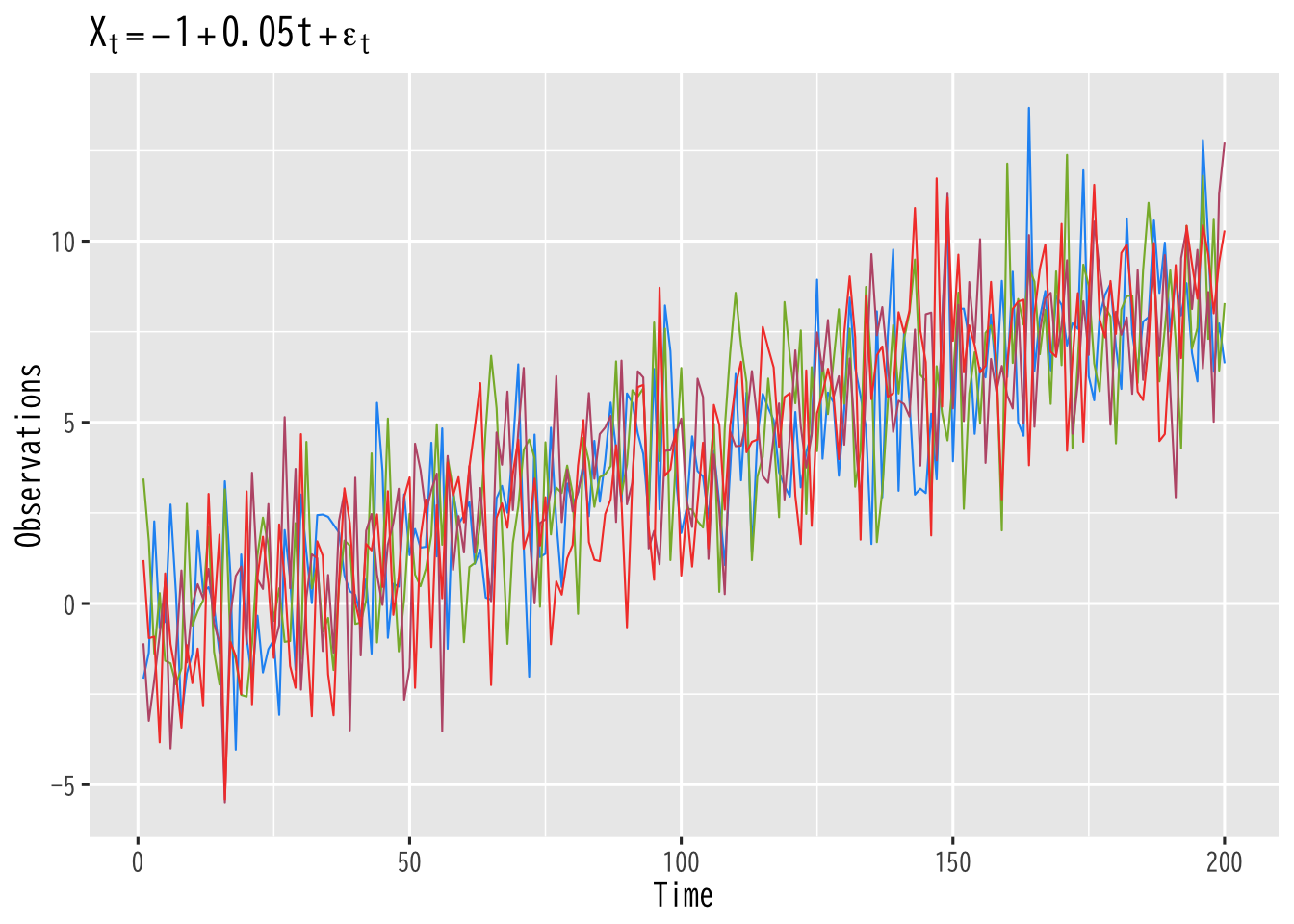
Figure 6: トレンドのあるホワイトノイズ
ランダムウォーク
定義
\(X_0\) を定数もしくは確率変数として 以下で帰納的に定義される確率過程
\begin{equation} X_{t}=X_{t-1}+\epsilon_{t}, \quad \epsilon_{t} \sim \mathrm{WN}(0,\sigma^2) \end{equation}- 分散 が時間とともに増加する時系列モデルの1つ
- 最も単純な 記憶 のあるモデル
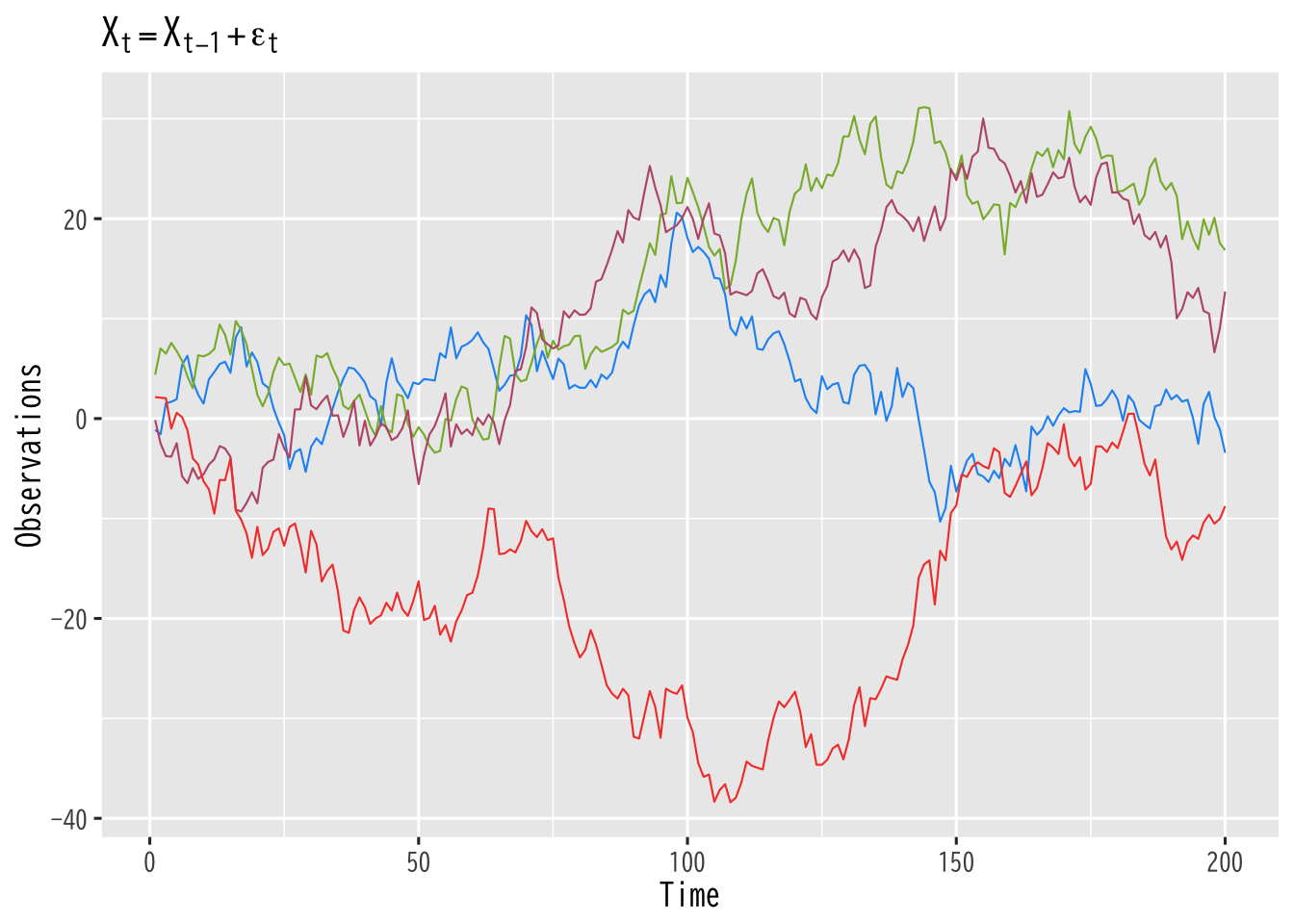
Figure 7: ランダムウォーク
演習
問題
- 以下の問に答えなさい
トレンドのあるホワイトノイズ\(X_{t}\)の
- 平均 \(\mathbb{E}[X_{t}]\)
- 分散 \(\mathrm{Var}(X_{t})\)
を求めなさい
- ランダムウォークの平均と分散を求めなさい
解答例
定義に従い計算する
\begin{align} \mathbb{E}[X_{t}] &= \mathbb{E}[\mu+\alpha t+\epsilon_{t}]\\ &= \mathbb{E}[\mu]+\mathbb{E}[\alpha t]+\mathbb{E}[\epsilon_{t}]\\ &= \mu+\alpha t\\ \mathrm{Var}(X_{t}) &= \mathrm{Var}(\mu+\alpha t+\epsilon_{t})\\ &= \mathrm{Var}(\mu)+\mathrm{Var}(\alpha t) +\mathrm{Var}(\epsilon_{t})\\ &= 0+0+\sigma^{2}\\ &= \sigma^{2} \end{align}
定義に従い帰納的に計算する
\begin{align} \mathbb{E}[X_{t}] &= \mathbb{E}[X_{t-1}+\epsilon_{t}]\\ &= \mathbb{E}[X_{t-1}]+\mathbb{E}[\epsilon_{t}]\\ &= \mathbb{E}[X_{1}]\\ \mathrm{Var}(X_{t}) &= \mathrm{Var}(X_{t-1}+\epsilon_{t})\\ &= \mathrm{Var}(X_{t-1})+\mathrm{Var}(\epsilon_{t})\\ &= \mathrm{Var}(X_{1})+(t-1)\cdot\sigma^{2} \end{align}
より一般的なモデル
自己回帰過程
定義 (AR(p); 次数 \(p\) の auto regressive の略)
\(a_1,\dotsc,a_p\)を定数とし \(X_1,\dotsc,X_p\)が初期値として与えられたとき 以下で帰納的に定義される確率過程
\begin{equation} X_{t}=a_1X_{t-1}+\cdots+a_pX_{t-p}+\epsilon_{t}, \quad \epsilon_{t} \sim \mathrm{WN}(0,\sigma^2) \end{equation}- ランダムウォークの一般化
- \(p=1, a_1=1\) かつ \(\epsilon_{t}\) が独立同分布ならランダムウォーク
- 忘却 しながら記憶するモデル (\(|a_i|<1\) などの条件が必要)
- ランダムウォークの一般化
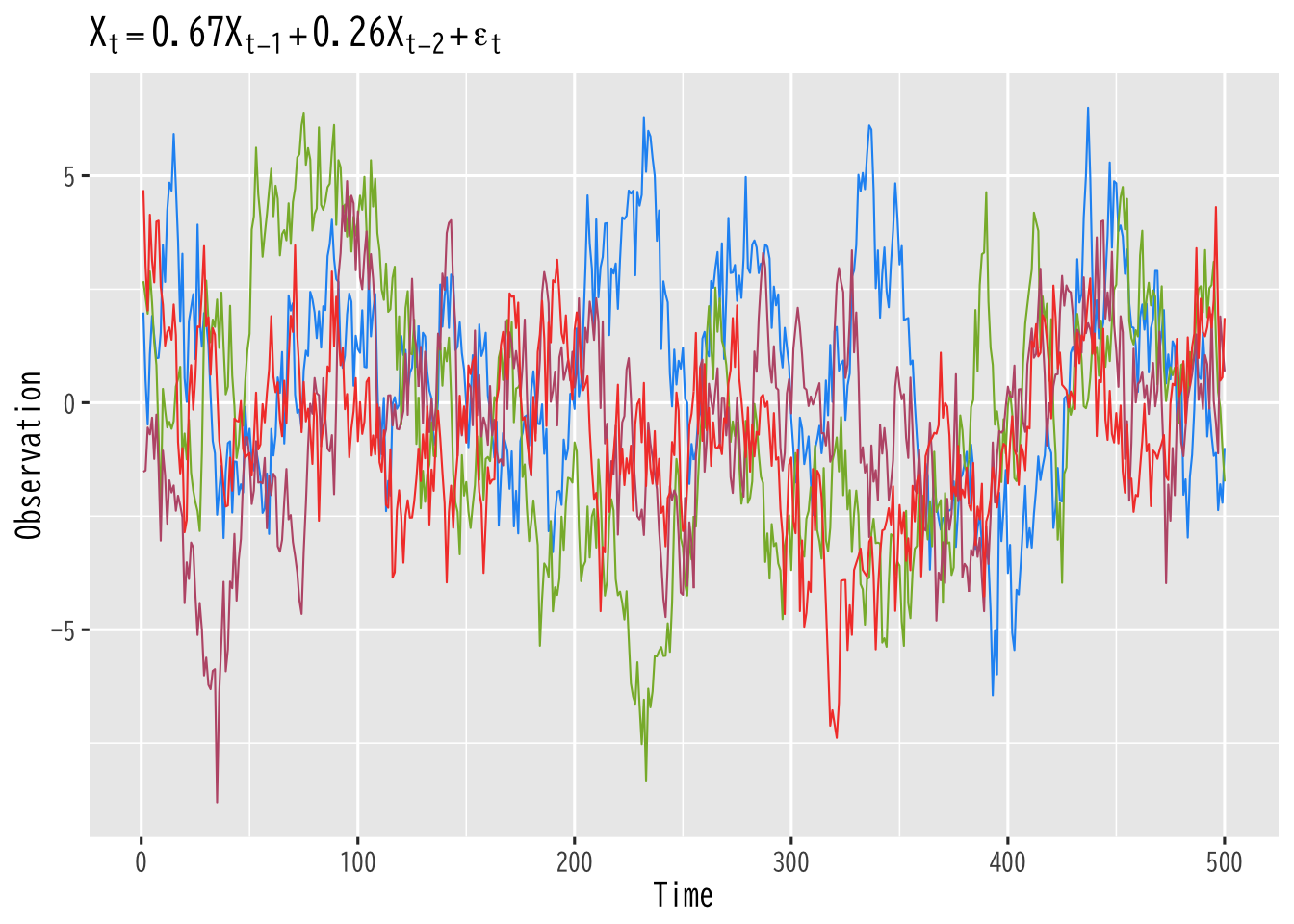
Figure 8: AR過程
移動平均過程
定義 (MA(q); 次数 \(q\) の moving average の略)
\(b_1,\dotsc,b_q\)を定数とし, \(X_1,\dotsc,X_q\)が初期値として与えられたとき 以下で帰納的に定義される確率過程
\begin{equation} X_{t} = b_1\epsilon_{t-1}+\cdots+b_q\epsilon_{t-q}+\epsilon_{t}, \quad \epsilon_{t} \sim \mathrm{WN}(0,\sigma^2) \end{equation}- 記憶のあるホワイトノイズ (構成する部品を記憶)
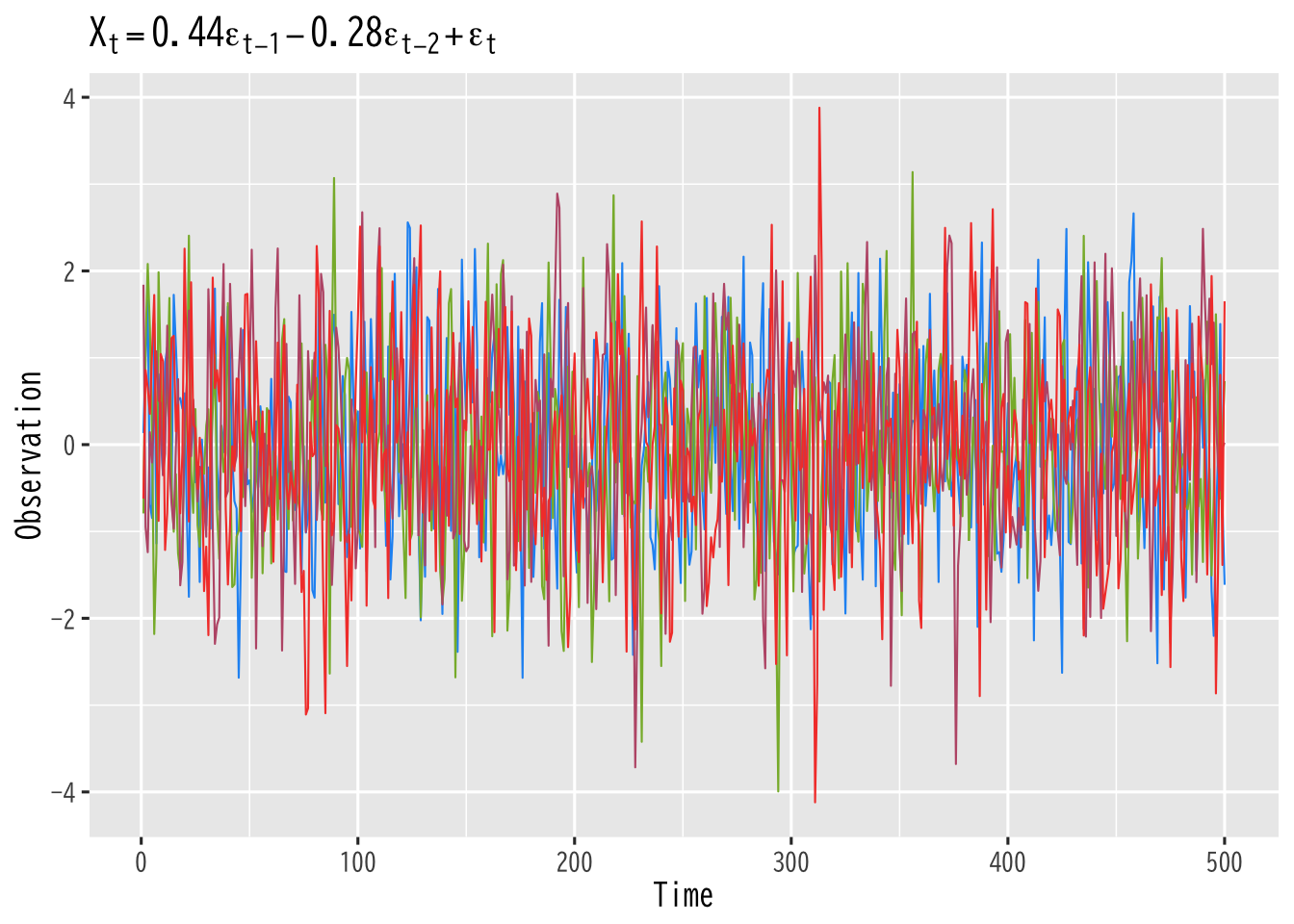
Figure 9: MA過程
自己回帰移動平均過程
定義 (ARMA(\(p,q\)); 次数 \((p,q)\))
\(a_1,\dotsc,a_p,b_1,\dotsc,b_q\) を定数とし \(X_1,\dotsc,X_{\max\{p,q\}}\) が初期値として与えられたとき 以下で帰納的に定まる確率過程
\begin{align} X_{t} &= a_1X_{t-1}+\cdots+a_pX_{t-p}\\ &\quad+ b_1\epsilon_{t-1}+\cdots+b_q\epsilon_{t-q} +\epsilon_{t},\\ &\quad \epsilon_{t} \sim \mathrm{WN}(0,\sigma^2) \end{align}- AR(\(p\))モデルはARMA(\(p,0\)),MA(\(q\))モデルはARMA(\(0,q\))
- 単純な形ながら異なる時点間の従属構造を柔軟に記述
- 基本的な時系列モデルとして広く利用されている
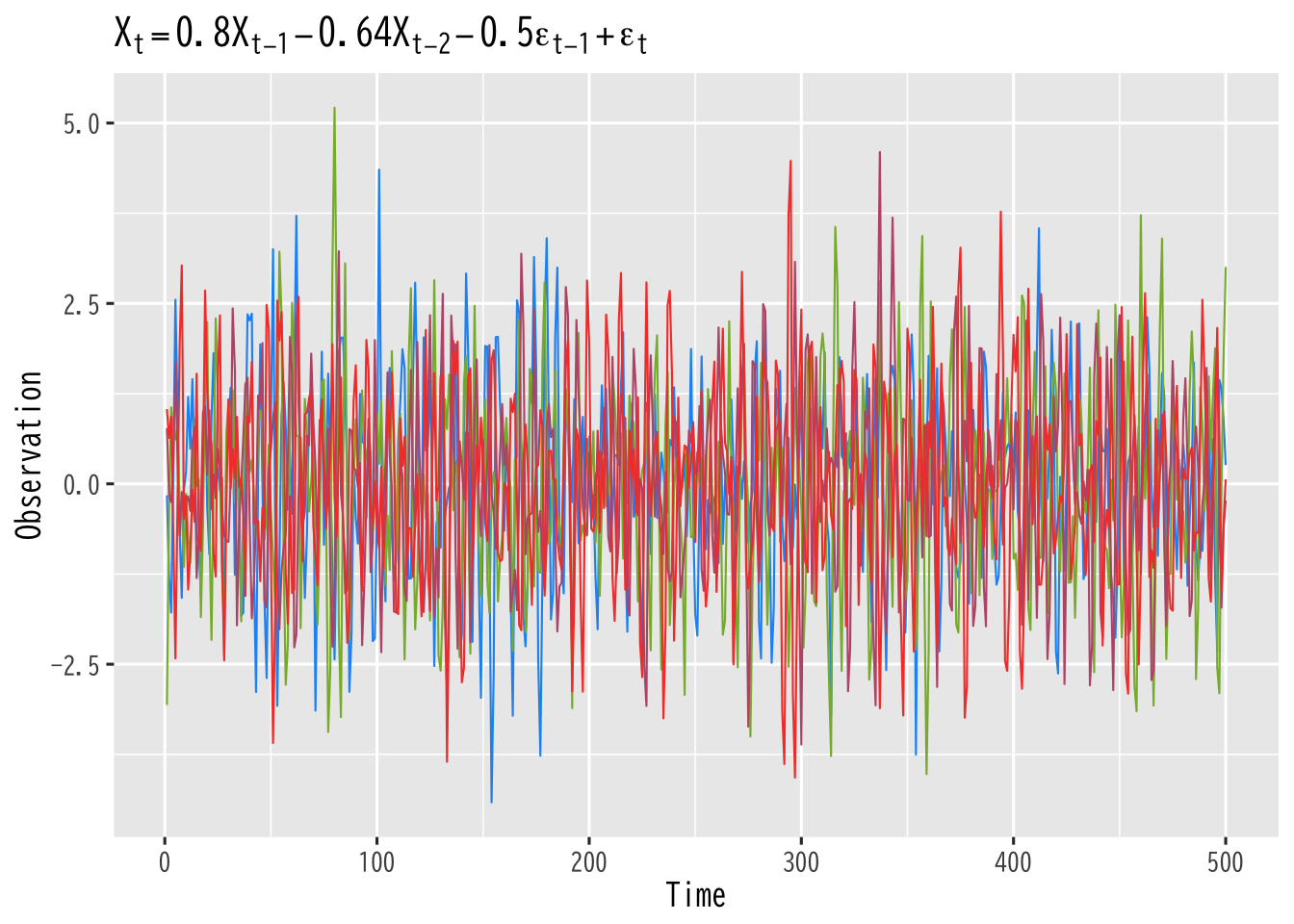
Figure 10: ARMA過程
演習
問題
- 以下の問に答えなさい
- AR(1)の平均と分散を求めなさい
- MA(1)の平均と分散を求めなさい
解答例
定義に従い帰納的に計算する
\begin{align} \mathbb{E}[X_{t}] &= \mathbb{E}[a_{1}X_{t-1}+\epsilon_{t}]\\ &= a_{1}\mathbb{E}[X_{t-1}]+\mathbb{E}[\epsilon_{t}]\\ &= a_{1}^{t-1}\mathbb{E}[X_{1}]\\ \mathrm{Var}(X_{t}) &= \mathrm{Var}(a_{1}X_{t-1}+\epsilon_{t})\\ &= a_{1}^{2}\mathrm{Var}(X_{t-1})+\mathrm{Var}(\epsilon_{t})\\ &= a_{1}^{2(t-1)}\mathrm{Var}(X_{1}) +\frac{1-a_{1}^{2(t-1)}}{1-a_{1}^{2}}\cdot\sigma^{2} \end{align}
定義に従い帰納的に計算する
\begin{align} \mathbb{E}[X_{t}] &= \mathbb{E}[b_{1}\epsilon_{t-1}+\epsilon_{t}]\\ &= b_{1}\mathbb{E}[\epsilon_{t-1}]+\mathbb{E}[\epsilon_{t}]\\ &= 0\\ \mathrm{Var}(X_{t}) &= \mathrm{Var}(b_{1}\epsilon_{t-1}+\epsilon_{t})\\ &= b_{1}^{2}\mathrm{Var}(\epsilon_{t-1})+\mathrm{Var}(\epsilon_{t})\\ &= (b_{1}^{2}+1)\cdot\sigma^{2} \end{align}
定常過程と非定常過程
弱定常性
- 確率過程\(X_{t},\;t=1,\dotsc,T\)が次の性質をもつ
\(X_{t}\)の平均は時点\(t\)によらない
\begin{equation} \mathbb{E}[X_{t}]=\mu \quad \text{(時間の添字を持たない)} \end{equation}\(X_{t}\)と\(X_{t+h}\)の共分散は時点\(t\)によらず時差\(h\)のみで定まる
\begin{equation} \mathrm{Cov}(X_{t},X_{t+h}) =\gamma(h) \quad \text{(時間の添字を持たない)} \end{equation}特に\(X_{t}\)の分散は時点\(t\)によらない (\(h=0\)の場合)
\begin{equation} \mathrm{Var}(X_{t}) =\gamma(0), \quad \text{(\(X_{t}\)は二乗可積分であることを仮定)} \end{equation}
定常性と非定常性
- 定常でない確率過程は 非定常 であるという
- いろいろな確率過程の定常性
- 定常 : ホワイトノイズ, MA
- 非定常 : トレンドのあるホワイトノイズ, ランダムウォーク
- 定常にも非定常にもなりうる : AR, ARMA
非定常過程の難しさ
- 性質を特徴付ける統計量が観測値から得られない
- 平均や分散などの基本的な統計量が時間によって変動する
- 1つの時系列から記述統計量の推測は一般にできない
- 擬似相関の問題
- 2つの独立なランダムウォークは高い確率で“相関”を持つ
- 独立な時系列にも関わらず見掛けの相関が現れることがある
- http://tylervigen.com/spurious-correlations
- 因果推論などの潜伏変数とは異なる問題
- 2つの独立なランダムウォークは高い確率で“相関”を持つ
非定常過程の取り扱い
- 定常過程とみなせるように変換して分析を実行
階差系列
ランダムウォークは階差をとればホワイトノイズ(定常過程)となる
\begin{equation} X_{t}=X_{t-1}+\epsilon_{t} \quad\Rightarrow\quad Y_{t}=X_{t}-X_{t-1}=\epsilon_{t} \end{equation}対数変換
対数変換と階差で微小な比率の変動を取り出すことができる
\begin{equation} X_{t}=(1+\epsilon_{t})X_{t-1} \quad\Rightarrow\quad Y_{t}=\log(X_{t})-\log(X_{t-1}) =\log(1+\epsilon_{t}) \simeq\epsilon_{t} \end{equation}トレンド成分+季節成分+変動成分への分解
適当な仮説のもとに取り扱いやすい成分の和に分解する
自己共分散・自己相関
自己共分散・自己相関
- 確率過程\(X_{t}\)が 定常過程 の場合
\(X_{t}\) と \(X_{t+h}\) の共分散は時点\(t\)によらずラグ\(h\)のみで定まる
自己共分散 (定常過程の性質よりラグは\(h\ge0\)を考えればよい)
\begin{equation} \mathrm{Cov}(X_{t},X_{t+h}) =\gamma(h) \end{equation}\(X_{t}\) と \(X_{t+h}\) の相関も\(t\)によらずラグ\(h\)のみで定まる
自己相関
\begin{equation} \mathrm{Cov}(X_{t},X_{t+h})/\mathrm{Var}(X_{t}) =\gamma(h)/\gamma(0) \end{equation}
- 異なる時点間での観測データの従属関係を要約する最も基本的な統計量
標本自己共分散・標本自己相関
- 観測データ \(X_1,\dotsc,X_{T}\) からの推定
ラグ\(h\)の自己共分散の推定 : 標本自己共分散
\begin{equation} \hat\gamma(h) = \frac{1}{T}\sum_{t=1}^{T-h}(X_{t}-\bar{X})(X_{t+h}-\bar{X}) \end{equation}\(\bar{X}=\frac{1}{T}\sum_{t=1}^TX_{t}\) は標本平均
ラグ\(h\)での自己相関の推定 : 標本自己相関
\begin{equation} \hat\gamma(h)/\hat\gamma(0) = \frac{\sum_{t=1}^{T-h}(X_{t}-\bar{X})(X_{t+h}-\bar{X})}{\sum_{t=1}^T(X_{t}-\bar{X})^2} \end{equation}
数値例
- 同じモデルに従うパス(系列)の自己相関を比較する
- 自己回帰過程 (AR過程)
- 移動平均過程 (MA過程)
- 自己回帰移動平均過程 (ARMA過程)
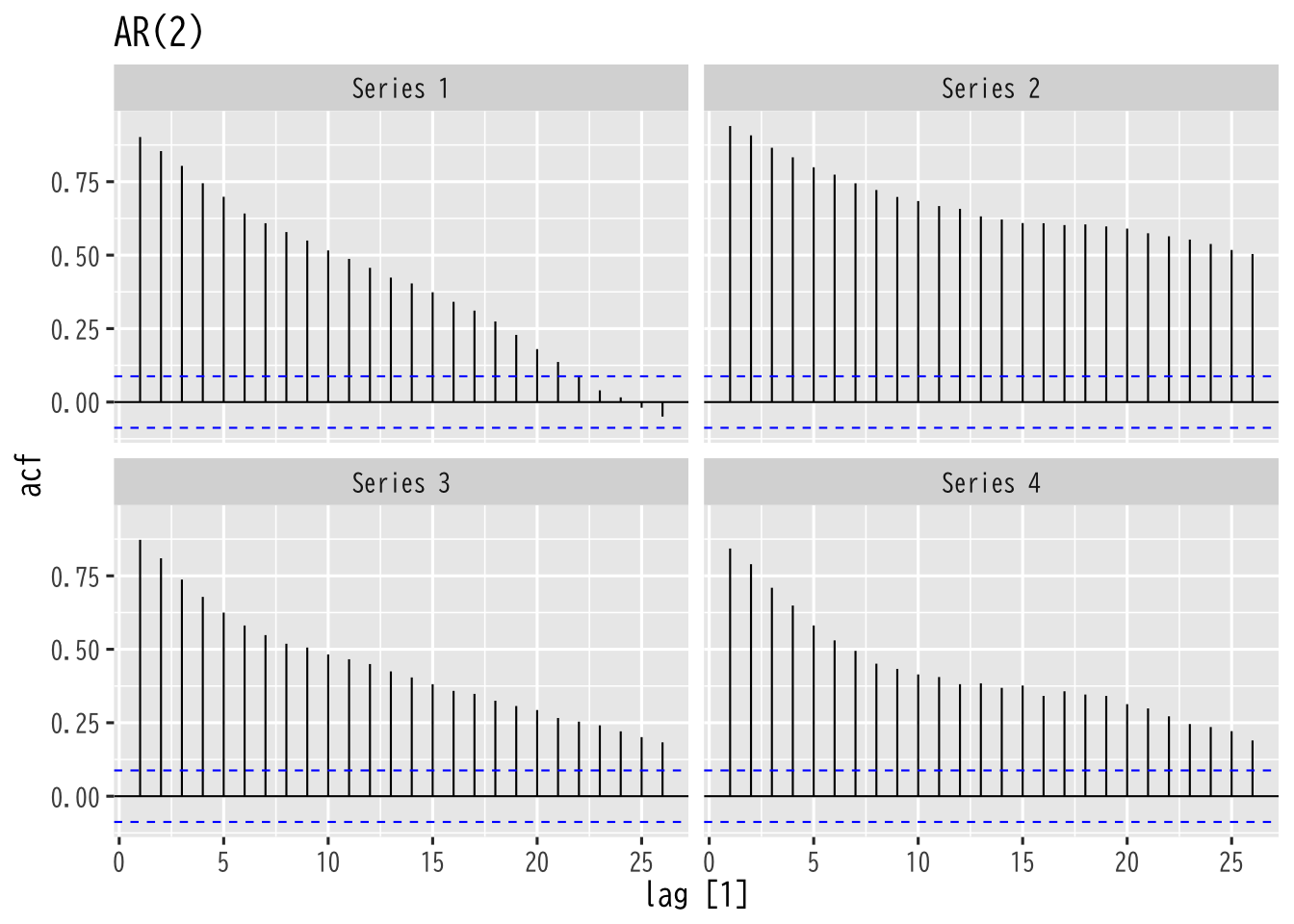
Figure 11: AR過程の自己相関
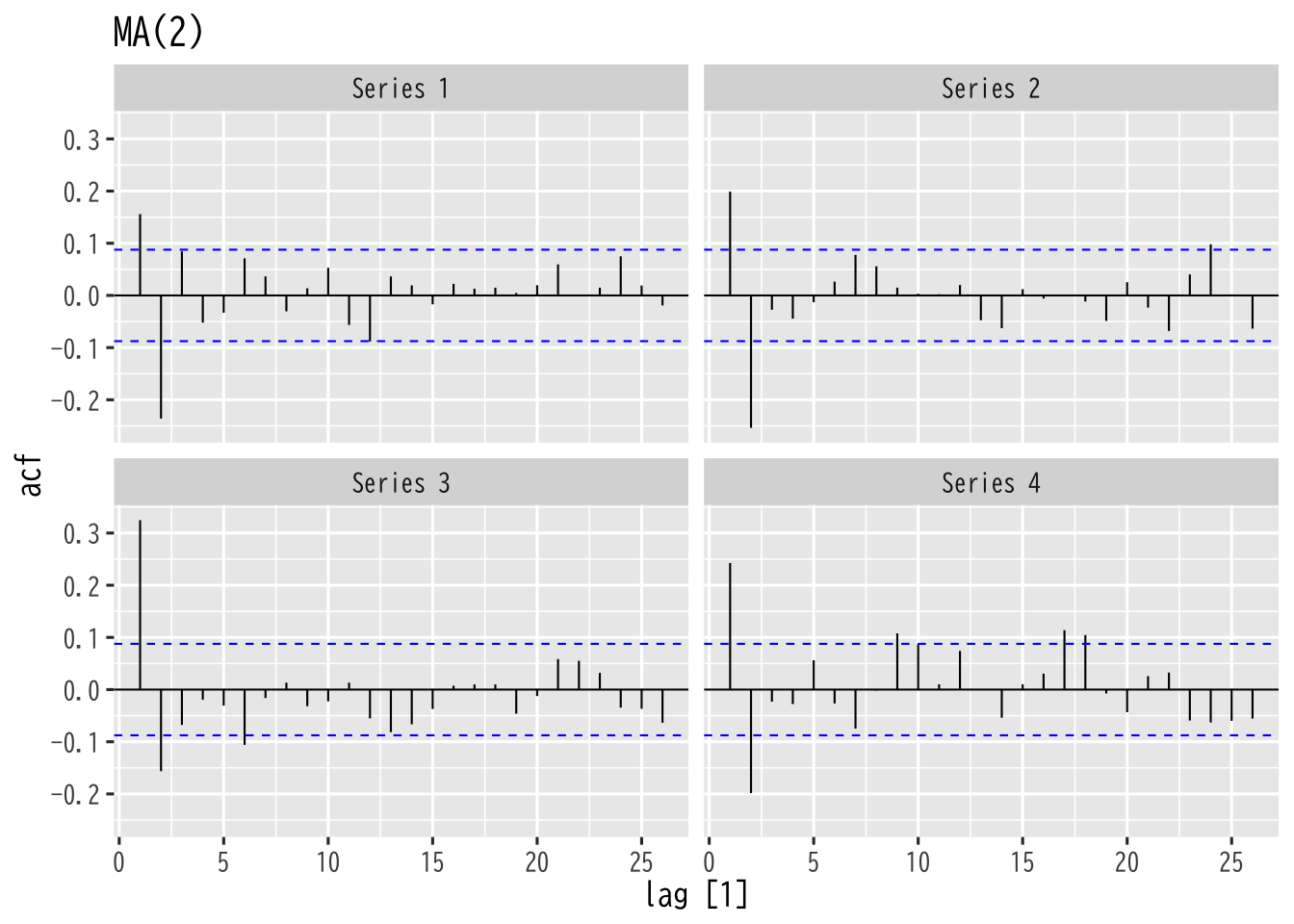
Figure 12: MA過程の自己相関
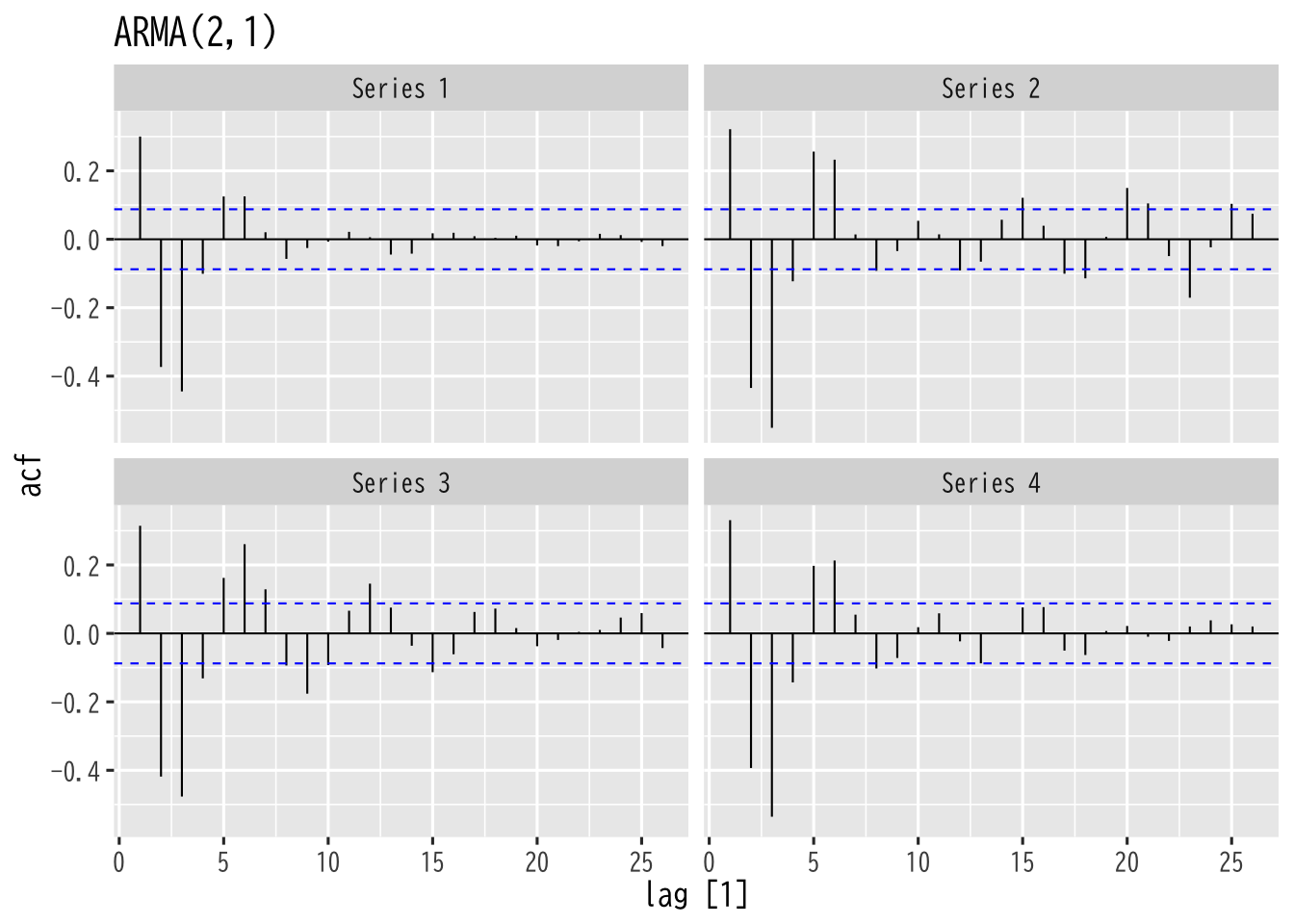
Figure 13: ARMA過程の自己相関
演習
問題
- 以下の問に答えなさい
- 定常なAR(\(p\))過程を考える. \(\mathbb{E}[X_{t}]=0\) であるとき, AR過程の係数と自己共分散の間に成り立つ関係を考えなさい
解答例
ラグ\(h>0\)の自己共分散を考える
\begin{align} \gamma(h) &= \mathbb{E}[X_{t}X_{t+h}]\\ &= \mathbb{E}[X_{t}(a_{1}X_{t+h-1}+\dotsb+a_{p}X_{t+h-p}+\epsilon_{t+h})]\\ &= a_{1}\mathbb{E}[X_{t}X_{t+h-1}] +\dotsb +a_{p}\mathbb{E}[X_{t}X_{t+h-p}] +\mathbb{E}[X_{t}\epsilon_{t+h}]\\ &= a_{1}\gamma(h-1) +\dotsb+ a_{p}\gamma(h-p) \end{align}
\(1\le h\le p\) を考えると以下の関係が成り立つ
\begin{equation} \begin{pmatrix} \gamma(1)\\ \gamma(2)\\ \vdots\\ \gamma(p) \end{pmatrix} = \begin{pmatrix} \gamma(0)&\gamma(-1)&\dots&\gamma(-p+1)\\ \gamma(1)&\gamma(0)&\dots&\gamma(-p+2)\\ \vdots&\vdots&\ddots&\vdots\\ \gamma(p-1)&\gamma(p-2)&\dots&\gamma(0) \end{pmatrix} \begin{pmatrix} a_{1}\\ a_{2}\\ \vdots\\ a_{p} \end{pmatrix} \end{equation}- Yule-Walker 方程式 という
- Yule-Walker方程式の性質
- 行列は Toeplitz 行列と呼ばれる
- \(\gamma(h)=\gamma(-h)\)より行列は対称行列
- 共分散の性質から行列は正定値 (非負定値)
- 行列が正則ならば AR 過程の係数は一意に決まる
- 特殊な形を利用した高速な解法としては Levinson–Durbin アルゴリズムが知られている
次回の内容
- 第1回 : 時系列の基本モデル
- 第2回 : モデルの推定と予測