回帰分析

予測と発展的なモデル

(Press ? for help, n and p for next and previous slide)

村田 昇

講義の内容

  • 第1回: 回帰モデルの考え方と推定
  • 第2回: モデルの評価
  • 第3回: モデルによる予測と発展的なモデル

回帰分析の復習

線形回帰モデル

  • 目的変数 を 説明変数 で説明する関係式を構成
    • 説明変数: \(x_1,\dotsc,x_p\) (p次元)
    • 目的変数: \(y\) (1次元)

  • 回帰係数 \(\beta_0,\beta_1,\dotsc,\beta_p\) を用いた一次式

    \begin{equation} y=\beta_0+\beta_1x_1+\dotsb+\beta_px_p \end{equation}

  • 誤差項 を含む確率モデルで観測データを表現

    \begin{equation} y_i=\beta_0+\beta_1 x_{i1}+\cdots+\beta_px_{ip}+\epsilon_i \quad (i=1,\dotsc,n) \end{equation}

問題設定

  • 確率モデル

    \begin{equation} \boldsymbol{y} =X\boldsymbol{\beta}+\boldsymbol{\epsilon}, \quad\boldsymbol{\epsilon}\sim\text{確率分布} \end{equation}

  • 式の評価 : 残差平方和 の最小化による推定

    \begin{equation} S(\boldsymbol{\beta}) =(\boldsymbol{y}-X\boldsymbol{\beta})^{\mathsf{T}} (\boldsymbol{y}-X\boldsymbol{\beta}) \end{equation}

解とその一意性

  • 解の条件 : 正規方程式

    \begin{equation} X^{\mathsf{T}}X\boldsymbol{\beta} =X^{\mathsf{T}}\boldsymbol{y} \end{equation}

  • 解の一意性 : Gram 行列 \(X^{\mathsf{T}}X\) が正則

    \begin{equation} \hat{\boldsymbol{\beta}} = (X^{\mathsf{T}}X)^{-1} X^{\mathsf{T}}\boldsymbol{y} \end{equation}

解析の事例

気温に影響を与える要因の分析

  • データの概要

    日付 気温 降雨 日射 降雪 風向 風速 気圧 湿度 雲量
    2024-10-01 23.3 0.5 11.45 0 NNW 2.6 1006.0 81 5.8
    2024-10-02 26.5 0.0 18.32 0 S 2.9 1007.9 77 6.0
    2024-10-03 23.1 11.0 5.88 0 E 2.7 1015.9 87 10.0
    2024-10-04 25.9 2.0 12.60 0 S 3.5 1015.4 87 10.0
    2024-10-05 21.3 9.5 1.88 0 NNE 2.5 1018.4 94 10.0
    2024-10-06 21.3 0.0 5.01 0 NNW 1.7 1017.1 93 10.0
    2024-10-07 25.0 0.0 14.99 0 S 2.9 1008.9 83 8.0
    2024-10-08 18.8 33.5 1.98 0 NE 3.0 1008.9 97 10.0
    2024-10-09 16.0 53.5 3.58 0 NNW 2.9 1009.3 93 10.0
    2024-10-10 17.8 0.0 7.52 0 NNW 2.6 1009.8 75 6.0
    2024-10-11 19.0 0.0 16.14 0 SSE 1.9 1013.1 69 7.5
    2024-10-12 20.6 0.0 16.44 0 N 1.9 1019.0 73 2.5
    2024-10-13 20.9 0.0 16.27 0 NNW 2.2 1021.1 70 0.8
    2024-10-14 20.8 0.0 16.02 0 NNW 2.3 1022.6 71 4.0
    2024-10-15 22.1 0.0 16.53 0 SSW 2.2 1020.3 72 3.8
  • 気温を説明する5種類の線形回帰モデルを検討
    • モデル1 : 気温 = F(気圧)
    • モデル2 : 気温 = F(日射)
    • モデル3 : 気温 = F(気圧, 日射)
    • モデル4 : 気温 = F(気圧, 日射, 湿度)
    • モデル5 : 気温 = F(気圧, 日射, 雲量)

分析の視覚化

  • 関連するデータの散布図

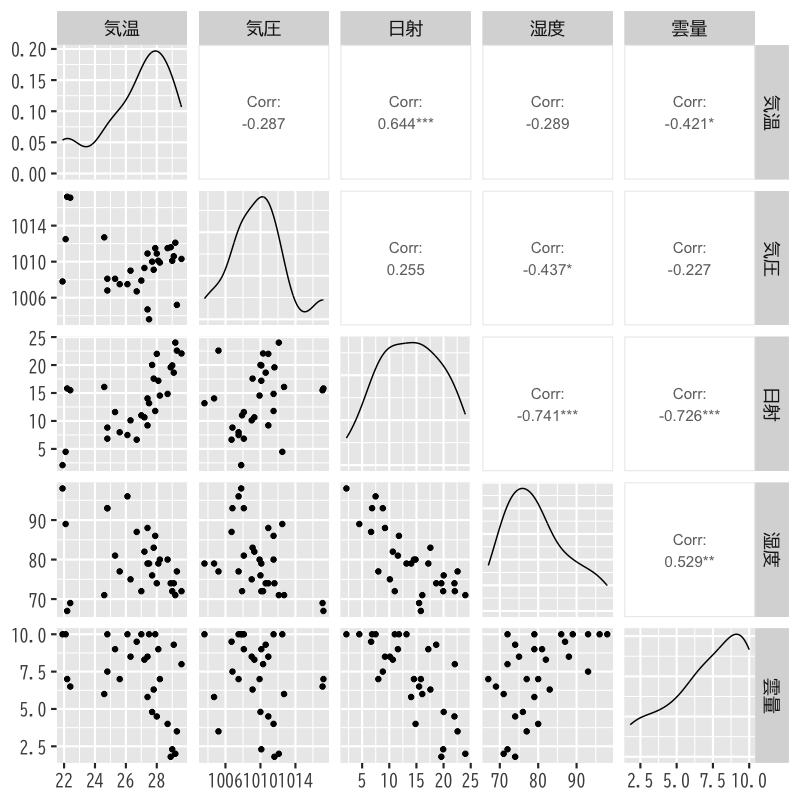
05_pairs.png

Figure 1: 気温,気圧,日射,湿度,雲量の関係

  • 観測値とあてはめ値の比較

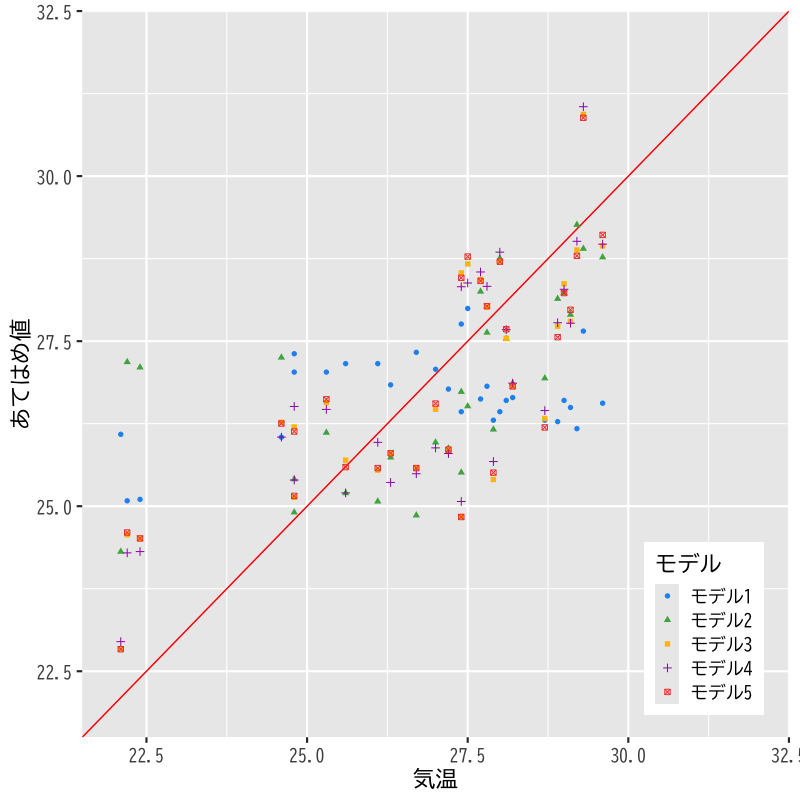
05_models.png

Figure 2: モデルの比較

寄与率

  • 決定係数 (R-squared)

    \begin{equation} R^2 = 1-\frac{\sum_{i=1}^n\hat{\epsilon}_i^2}{\sum_{i=1}^n(y_i-\bar{y})^2} \end{equation}

  • 自由度調整済み決定係数 (adjusted R-squared)

    \begin{equation} \bar{R}^2 = 1-\frac{\frac{1}{n{-}p{-}1}\sum_{i=1}^n\hat{\epsilon}_i^2} {\frac{1}{n{-}1}\sum_{i=1}^n(y_i-\bar{y})^2} \end{equation}
    • 不偏分散で補正

モデルの評価

  • 決定係数(\(R^{2}\)・ Adjusted \(R^{2}\))によるモデルの比較

    変数
    モデル1
    モデル2
    モデル3
    モデル4
    モデル5
    係数(SE)1 係数(SE)1 係数(SE)1 係数(SE)1 係数(SE)1
    気圧 -0.14(0.090)
    		-0.17(0.086) 0.06(0.088) -0.14(0.086)
    日射
    		0.17(0.101) 0.21(0.098)* 0.53(0.109)*** 0.38(0.146)*
    湿度


    		0.28(0.067)***
    雲量



    		0.49(0.306)
    R² 0.078 0.093 0.204 0.519 0.272
    Adjusted R² 0.047 0.062 0.147 0.466 0.191
    1 *p<0.05; **p<0.01; ***p<0.001
    Abbreviation: SE = 標準誤差

\(F\)統計量による検定

  • 説明変数のうち1つでも役に立つか否かを検定する
    • 帰無仮説 \(H_{0}\): \(\beta_1=\dotsb=\beta_p=0\)
    • 対立仮説 \(H_{1}\): \(\exists j\;\beta_j\neq0\) (少なくとも1つは役に立つ)

  • \(F\)統計量: 決定係数(または残差)を用いて計算

    \begin{equation} F =\frac{n{-}p{-}1}{p}\frac{R^2}{1-R^2} \end{equation}
  • \(p\)値: 自由度 \(p,n{-}p{-}1\) の \(F\)分布で計算

モデルの評価

  • \(F\)統計量によるモデルの比較

    変数
    モデル1
    モデル2
    モデル3
    モデル4
    モデル5
    係数(SE)1 係数(SE)1 係数(SE)1 係数(SE)1 係数(SE)1
    気圧 -0.14(0.090)
    		-0.17(0.086) 0.06(0.088) -0.14(0.086)
    日射
    		0.17(0.101) 0.21(0.098)* 0.53(0.109)*** 0.38(0.146)*
    湿度


    		0.28(0.067)***
    雲量



    		0.49(0.306)
    R² 0.078 0.093 0.204 0.519 0.272
    Statistic 2.47 2.98 3.58 9.72 3.36
    p-value 0.13 0.10 0.041 <0.001 0.033
    1 *p<0.05; **p<0.01; ***p<0.001
    Abbreviation: SE = 標準誤差

\(t\)統計量による検定

  • 回帰係数 \(\beta_j\) が回帰式に寄与するか否かを検定する
    • 帰無仮説 \(H_{0}\): \(\beta_j=0\)
    • 対立仮説 \(H_{1}\): \(\beta_j\neq0\) (\(\beta_j\) は役に立つ)

  • \(t\)統計量: 各係数ごと，\(\zeta\) は \((X^{\mathsf{T}} X)^{-1}\) の対角成分

    \begin{equation} t=\frac{\hat{\beta}_j}{\hat{\sigma}\zeta_{j}} \end{equation}
  • \(p\)値: 自由度 \(n{-}p{-}1\) の \(t\)分布を用いて計算

モデルの評価

  • \(t\)統計量によるモデルの比較

    変数
    モデル3
    モデル4
    モデル5
    係数 SE t統計量 p値1 係数 SE t統計量 p値1 係数 SE t統計量 p値1
    (Intercept) 191 87.3 2.19 0.037* -70 92.9 -0.757 0.5 156 87.8 1.78 0.087
    気圧 -0.17 0.086 -1.97 0.059 0.06 0.088 0.715 0.5 -0.14 0.086 -1.64 0.11
    日射 0.21 0.098 2.10 0.045* 0.53 0.109 4.85 <0.001*** 0.38 0.146 2.61 0.015*
    湿度



    		0.28 0.067 4.21 <0.001***



    雲量







    		0.49 0.306 1.59 0.12
    1 *p<0.05; **p<0.01; ***p<0.001
    Abbreviation: SE = 標準誤差

診断プロットによる評価

  • 回帰モデルのあてはまりを視覚的に評価
    • Residuals vs Fitted: あてはめ値(予測値)と残差の関係
      (誤差の均一性)
    • Normal Q-Q: 標準化残差と標準正規分布の比較
      (残差の正規性)
    • Scale-Location: あてはめ値と標準化残差の関係
      (分散の均一性)
    • Residuals vs Leverage: 標準化残差とテコ比の関係
      (外れ値)

  • モデル3

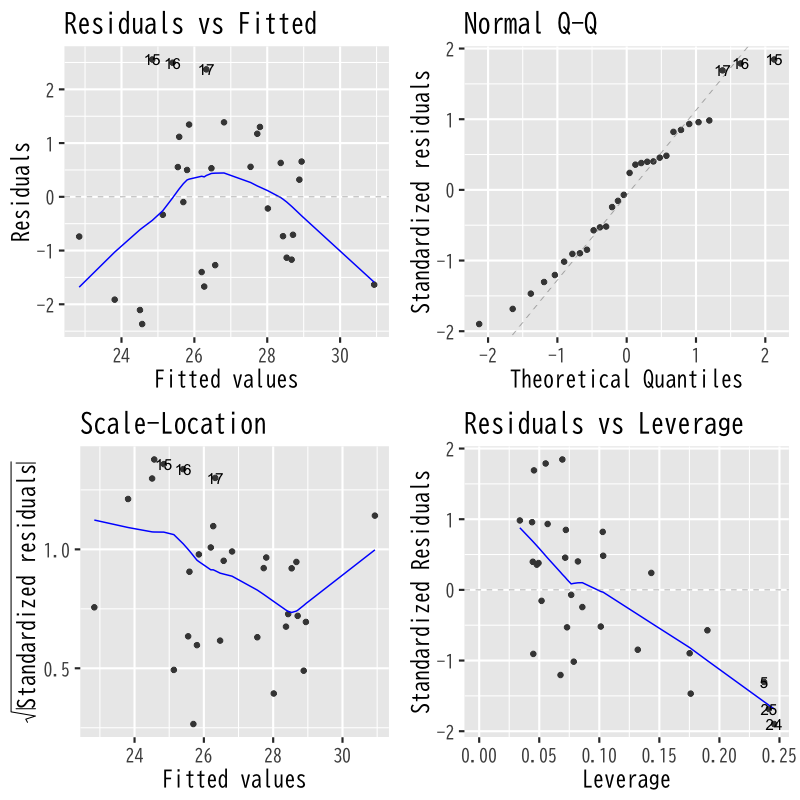
05_diag_model3.png

Figure 3: モデル3の診断

  • モデル4

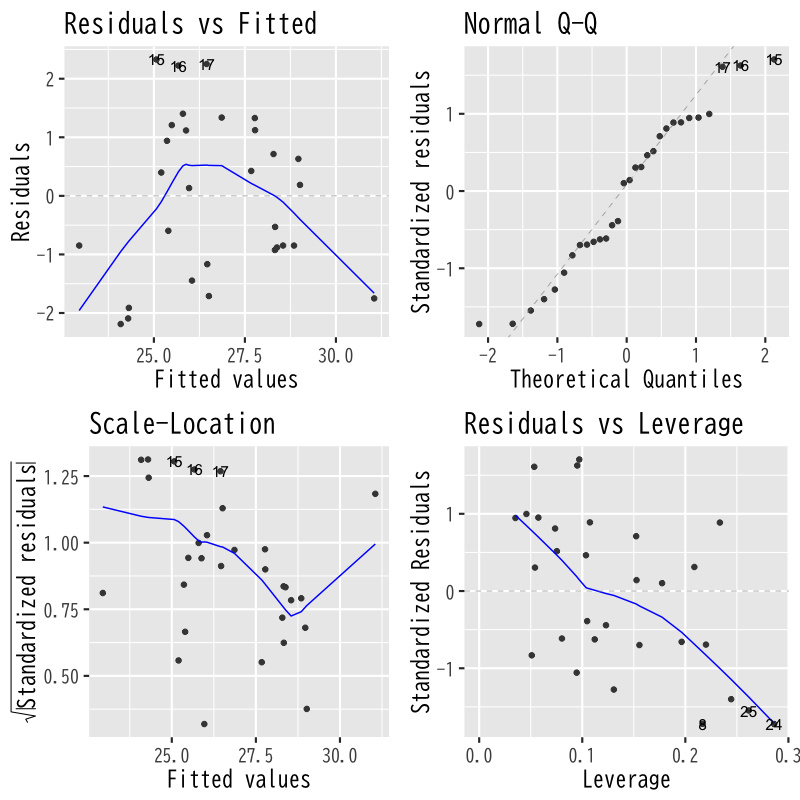
05_diag_model4.png

Figure 4: モデル4の診断

  • モデル5

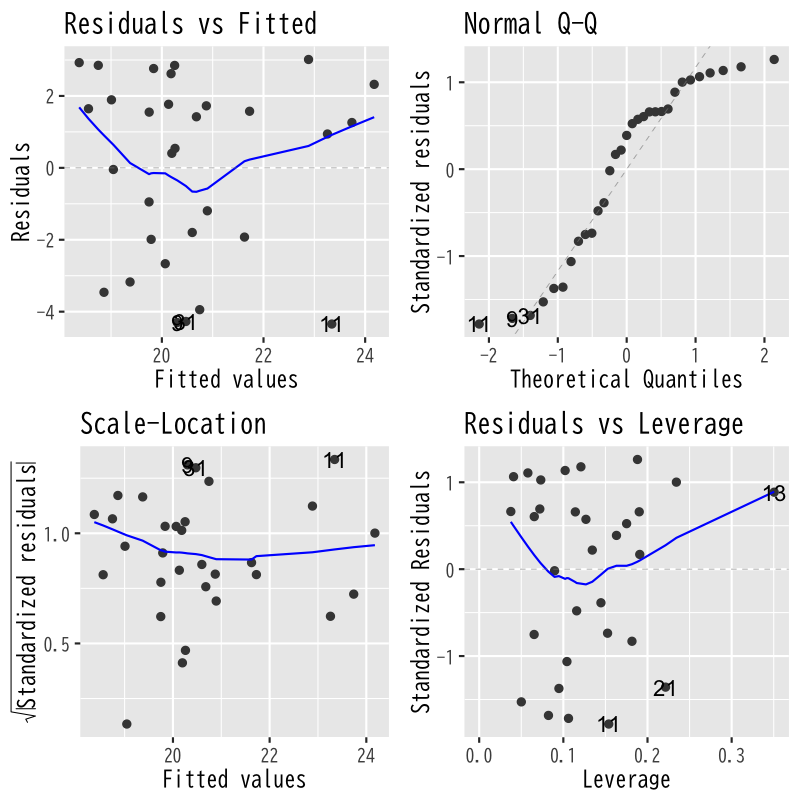
05_diag_model5.png

Figure 5: モデル5の診断

回帰モデルによる予測

予測

  • 新しいデータ (説明変数) \(\boldsymbol{x}\) に対する 予測値

    \begin{equation} \hat{y} = (1,\boldsymbol{x}^{\mathsf{T}})\hat{\boldsymbol{\beta}}, \qquad \hat{\boldsymbol{\beta}} = (X^{\mathsf{T}}X)^{-1} X^{\mathsf{T}}\boldsymbol{y} \end{equation}

  • 予測値は元データの目的変数の重み付け線形和

    \begin{equation} \hat{y} = \boldsymbol{w}(\boldsymbol{x})^{\mathsf{T}}\boldsymbol{y}, \qquad \boldsymbol{w}(\boldsymbol{x})^{\mathsf{T}} = (1,\boldsymbol{x}^{\mathsf{T}}) (X^{\mathsf{T}}X)^{-1} X^{\mathsf{T}} \end{equation}
    • 重みは元データと新規データの説明変数で決定

予測値の性質

  • 推定量は以下の性質をもつ多変量正規分布

    \begin{align} \mathbb{E}[\hat{\boldsymbol{\beta}}] &=\boldsymbol{\beta}\\ \mathrm{Cov}(\hat{\boldsymbol{\beta}}) &=\sigma^{2}(X^{\mathsf{T}}X)^{-1} \end{align}

  • この性質を利用して以下の3つの値の違いを評価

    \begin{align} y&=(1,\boldsymbol{x}^{\mathsf{T}})\boldsymbol{\beta}+\epsilon &&\text{(観測値)}\\ \tilde{y}&=(1,\boldsymbol{x}^{\mathsf{T}})\boldsymbol{\beta} &&\text{(最適な予測値)}\\ \hat{y}&=(1,\boldsymbol{x}^{\mathsf{T}})\hat{\boldsymbol{\beta}} &&\text{(回帰式による予測値)} \end{align}
    • \(\hat{y}\) と \(y\) は独立な正規分布に従うことに注意

演習

問題

  • 誤差が平均0 分散 \(\sigma^{2}\) の正規分布に従うとき， 以下の問に答えなさい
    • 予測値 \(\hat{y}\) の平均を求めよ
    • 予測値 \(\hat{y}\) の分散を求めよ

解答例

  • 定義にもとづいて計算する

    \begin{align} \mathbb{E}[\hat{y}] &= \mathbb{E}[(1,\boldsymbol{x}^{\mathsf{T}})\hat{\boldsymbol{\beta}}]\\ &= (1,\boldsymbol{x}^{\mathsf{T}})\mathbb{E}[\hat{\boldsymbol{\beta}}]\\ &= (1,\boldsymbol{x}^{\mathsf{T}})\boldsymbol{\beta}\\ &= \tilde{y} \end{align}
    • 真の回帰式による最適な予測値

  • 定義にもとづいて計算する

    \begin{align} \mathrm{Var}(\hat{y}) &= \mathrm{Var}((1,\boldsymbol{x}^{\mathsf{T}}) (\hat{\boldsymbol{\beta}}-\boldsymbol{\beta}))\\ &= (1,\boldsymbol{x}^{\mathsf{T}}) \mathrm{Cov}(\hat{\boldsymbol{\beta}}-\boldsymbol{\beta}) (1,\boldsymbol{x}^{\mathsf{T}})^{\mathsf{T}}\\ &= (1,\boldsymbol{x}^{\mathsf{T}}) \mathrm{Cov}(\hat{\boldsymbol{\beta}}) (1,\boldsymbol{x}^{\mathsf{T}})^{\mathsf{T}}\\ &= (1,\boldsymbol{x}^{\mathsf{T}}) \sigma^{2} (X^{\mathsf{T}}X)^{-1} (1,\boldsymbol{x}^{\mathsf{T}})^{\mathsf{T}}\\ &= \sigma^{2} (1,\boldsymbol{x}^{\mathsf{T}}) (X^{\mathsf{T}}X)^{-1} (1,\boldsymbol{x}^{\mathsf{T}})^{\mathsf{T}} \end{align}

信頼区間

最適な予測値との差

  • 差の分布は以下の平均・分散をもつ正規分布に従う

    \begin{align} \mathbb{E}[\tilde{y}-\hat{y}] &=(1,\boldsymbol{x}^{\mathsf{T}})\boldsymbol{\beta} -(1,\boldsymbol{x}^{\mathsf{T}})\mathbb{E}[\hat{\boldsymbol{\beta}}] =0\\ \mathrm{Var}(\tilde{y}-\hat{y}) &=\underbrace{\sigma^{2}(1,\boldsymbol{x}^{\mathsf{T}})(X^{\mathsf{T}}X)^{-1} (1,\boldsymbol{x}^{\mathsf{T}})^{\mathsf{T}}}_{\text{\(\hat{\boldsymbol{\beta}}\)の推定誤差による分散}} =\sigma^{2}\gamma_{c}(\boldsymbol{x})^{2} \end{align}

  • 標準化による表現

    \begin{equation} \frac{\tilde{y}-\hat{y}}{\sigma\gamma_{c}(\boldsymbol{x})} \sim \mathcal{N}(0,1) \end{equation}

信頼区間

  • 未知の分散を不偏分散で推定

    \begin{equation} Z= \frac{\tilde{y}-\hat{y}}{\hat{\sigma}\gamma_{c}(\boldsymbol{x})} \sim \mathcal{T}(n{-}p{-}1) \quad (\text{\(t\)分布}) \end{equation}

  • 確率 \(\alpha\) の信頼区間

    \begin{equation} \mathcal{I}^{c}_{\alpha} = \left( \hat{y}-C_{\alpha}\hat{\sigma}\gamma_{c}(\boldsymbol{x}),\; \hat{y}+C_{\alpha}\hat{\sigma}\gamma_{c}(\boldsymbol{x}) \right) \end{equation}
    \begin{equation} P(|Z| < {C_{\alpha}} | Z\sim\mathcal{T}(n{-}p{-}1)) =\alpha \end{equation}
    • 最適な予測値 \(\tilde{y}\) が入ることが期待される区間

演習

問題

  • 以下の問に答えなさい

    • 信頼区間について以下の式が成り立つことを示せ

      \begin{equation} P(\tilde{y}\in\mathcal{I}^{c}_{\alpha}) =\alpha \end{equation}
    • 観測値と予測値の差 \(y-\hat{y}\) の平均と分散を求めよ

解答例

  • \(C_{\alpha}\) の定義にもとづいて計算すればよい

    \begin{align} \alpha &= P(|Z| < {C_{\alpha}})\\ &= P\left( \left|\frac{\tilde{y}-\hat{y}}{\hat{\sigma}\gamma_{c}(\boldsymbol{x})}\right| < {C_{\alpha}} \right)\\ &= P\left( |\tilde{y}-\hat{y}| < C_{\alpha}\hat{\sigma}\gamma_{c}(\boldsymbol{x}) \right)\\ &= P\left( -C_{\alpha}\hat{\sigma}\gamma_{c}(\boldsymbol{x}) < \tilde{y}-\hat{y} < C_{\alpha}\hat{\sigma}\gamma_{c}(\boldsymbol{x}) \right)\\ &= P\left( \hat{y}-C_{\alpha}\hat{\sigma}\gamma_{c}(\boldsymbol{x}) < \tilde{y} < \hat{y}+C_{\alpha}\hat{\sigma}\gamma_{c}(\boldsymbol{x}) \right) \end{align}

  • 独立性を利用して計算する

    \begin{align} \mathbb{E}[y-\hat{y}] &= \mathbb{E}[y] -\mathbb{E}[\hat{y}]\\ &= \tilde{y}-\tilde{y}\\ &= 0\\ \mathrm{Var}(y-\hat{y}) &= \mathrm{Var}(y) +\mathrm{Var}(\hat{y})\\ &= \sigma^{2} + \sigma^{2} (1,\boldsymbol{x}^{\mathsf{T}}) (X^{\mathsf{T}}X)^{-1} (1,\boldsymbol{x}^{\mathsf{T}})^{\mathsf{T}} \end{align}

予測区間

観測値との差

  • 差の分布は以下の平均・分散をもつ正規分布に従う

    \begin{align} \mathbb{E}[y-\hat{y}] &=(1,\boldsymbol{x}^{\mathsf{T}})\boldsymbol{\beta} +\mathbb{E}[\boldsymbol{\epsilon}] -(1,\boldsymbol{x}^{\mathsf{T}}) \mathbb{E}[\hat{\boldsymbol{\beta}}] =0\\ \mathrm{Var}(y-\hat{y}) &=\underbrace{\sigma^{2} (1,\boldsymbol{x}^{\mathsf{T}})(X^{\mathsf{T}}X)^{-1} (1,\boldsymbol{x}^{\mathsf{T}})^{\mathsf{T}} }_{\text{\(\hat{\boldsymbol{\beta}}\)の推定誤差による分散}} +\underbrace{\sigma^{2}}_{\text{誤差の分散}} =\sigma^{2}\gamma_{p}(\boldsymbol{x})^{2} \end{align}

  • 標準化による表現

    \begin{equation} \frac{y-\hat{y}}{\sigma\gamma_{p}(\boldsymbol{x})} \sim \mathcal{N}(0,1) \end{equation}

予測区間

  • 未知の分散を不偏分散で推定

    \begin{equation} Z= \frac{y-\hat{y}}{\hat{\sigma}\gamma_{p}(\boldsymbol{x})} \sim \mathcal{T}(n{-}p{-}1) \quad (\text{\(t\)分布}) \end{equation}

  • 確率 \(\alpha\) の予測区間

    \begin{equation} \mathcal{I}^{p}_{\alpha} = \left( \hat{y}-C_{\alpha}\hat{\sigma}\gamma_{p}(\boldsymbol{x}),\; \hat{y}+C_{\alpha}\hat{\sigma}\gamma_{p}(\boldsymbol{x}) \right) \end{equation}
    \begin{equation} P(|Z| < {C_{\alpha}} | Z\sim\mathcal{T}(n{-}p{-}1)) =\alpha \end{equation}
    • 観測値 \(y\) が入ることが期待される区間
    • \(\gamma_{p}>\gamma_{c}\) なので信頼区間より広くなる

解析の事例

信頼区間と予測区間

  • 東京の気候データを用いて以下を試みる

    • 8月のデータで回帰式を推定する

      気温 = F(気圧, 日射, 湿度)

    • 上記のモデルで9月のデータを予測する

  • 推定されたモデル

    変数 係数 SE t統計量 p値1
    (Intercept) 69 29.4 2.36 0.026*
    日射 0.02 0.045 0.409 0.7
    気圧 -0.03 0.030 -1.00 0.3
    湿度 -0.13 0.031 -4.06 <0.001***
    1 *p<0.05; **p<0.01; ***p<0.001
    Abbreviation: SE = 標準誤差

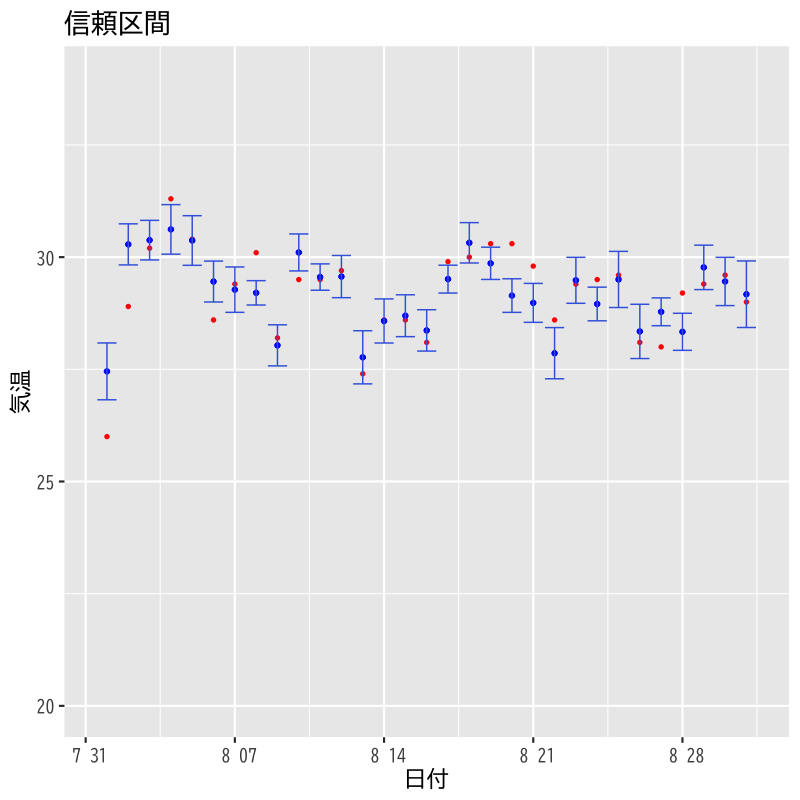
05_aug_cint.png

Figure 6: 8月のあてはめ値の信頼区間

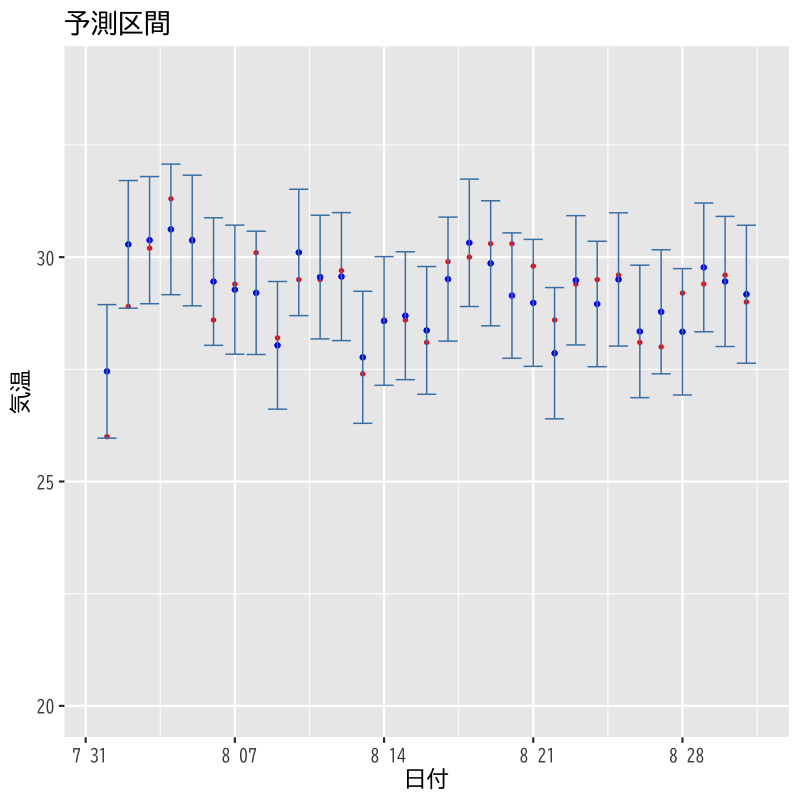
05_aug_pred.png

Figure 7: 8月のあてはめ値の予測区間

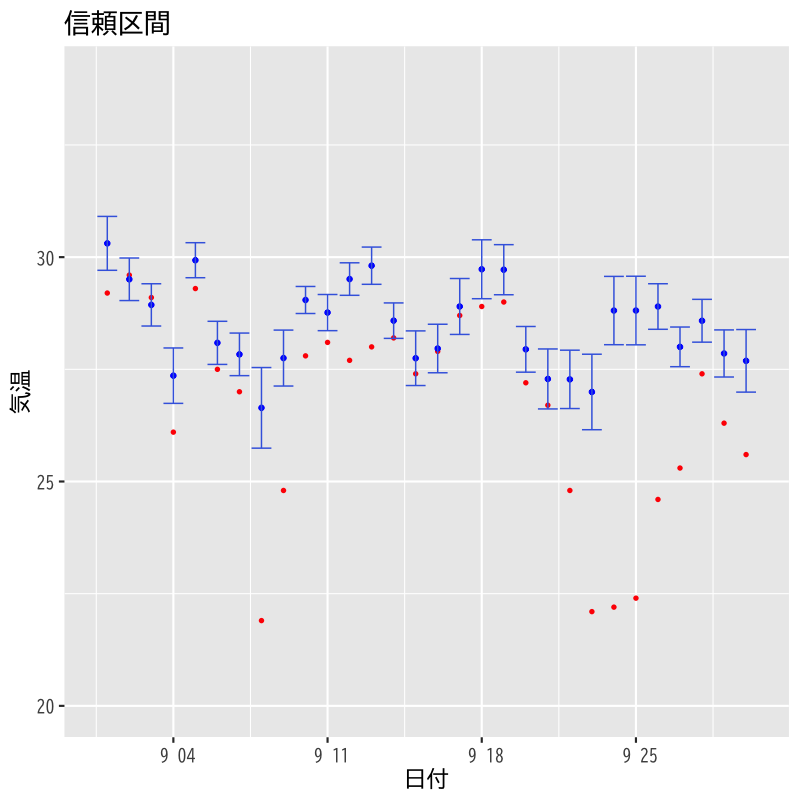
05_sep_cint.png

Figure 8: 8月モデルによる9月の予測値の信頼区間

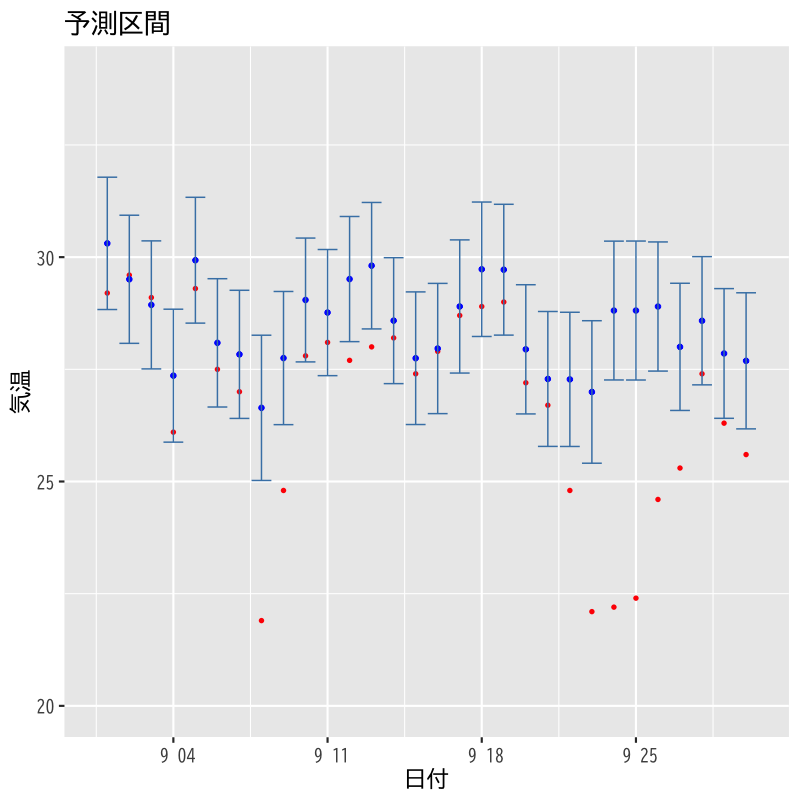
05_sep_pint.png

Figure 9: 8月モデルによる9月の予測値の予測区間

発展的なモデル

非線形性を含むモデル

  • 目的変数 \(y\)
  • 説明変数 \(x_1,\dotsc,x_p\)
  • 説明変数の追加で対応可能
    • 交互作用 (交差項) : \(x_ix_j\) のような説明変数の積
    • 非線形変換 : \(\log(x_k)\) のような関数による変換

カテゴリカル変数を含むモデル

  • 数値ではないデータ
    • 悪性・良性
    • 血液型 (A型,B型,AB型,O型)
  • 適切な方法で数値に変換して対応
    • 2値の場合は 1,0 (真，偽) を割り当てる
      • 悪性 : 1
      • 良性 : 0
    • 3値以上の場合は ダミー変数 を利用する (カテゴリ数-1個)
      • A型 : (1,0,0)
      • B型 : (0,1,0)
      • O型 : (0,0,1)
      • AB型 : (0,0,0)

解析の事例

非線形変換による線形化

body brain
Mountain beaver 1.35 8.1
Cow 465.00 423.0
Grey wolf 36.33 119.5
Goat 27.66 115.0
Guinea pig 1.04 5.5
Dipliodocus 11700.00 50.0
Asian elephant 2547.00 4603.0
Donkey 187.10 419.0
Horse 521.00 655.0
Potar monkey 10.00 115.0
Cat 3.30 25.6
Giraffe 529.00 680.0
Gorilla 207.00 406.0
Human 62.00 1320.0
  • 様々な動物の体重と脳の重さの関係を調べる
    • 体重は5桁程度のばらつき
    • 脳の重さは4桁程度のばらつき
  • 以下の変換を検討する
    • 変換なし
    • 体重を対数変換
    • 体重および脳の重さを対数変換

  • 散布図 (変換なし)

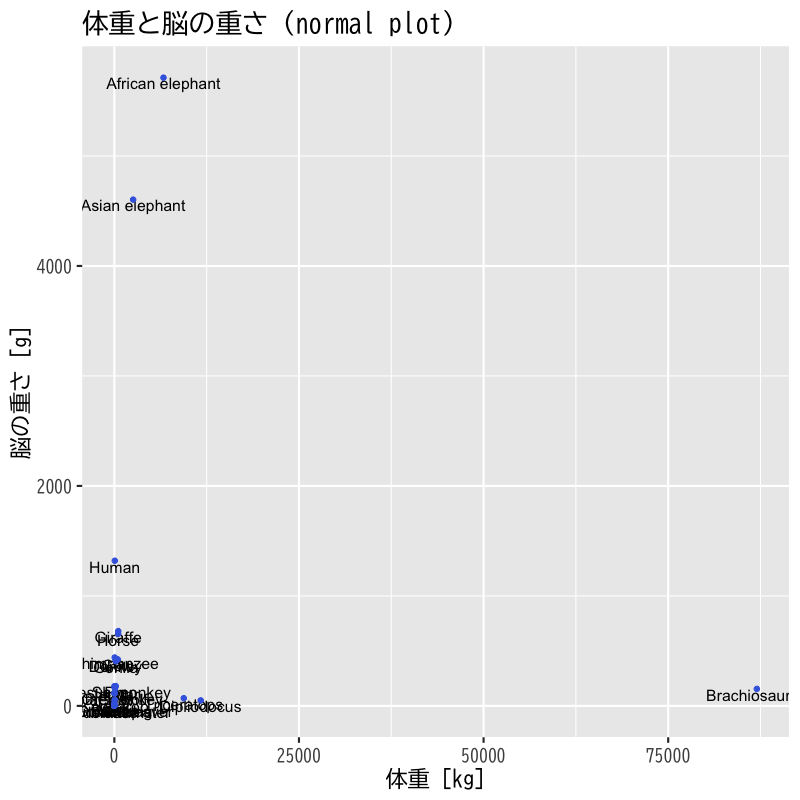
05_animals1.png

Figure 10: データの変換なし

  • 散布図 (x軸を対数変換)

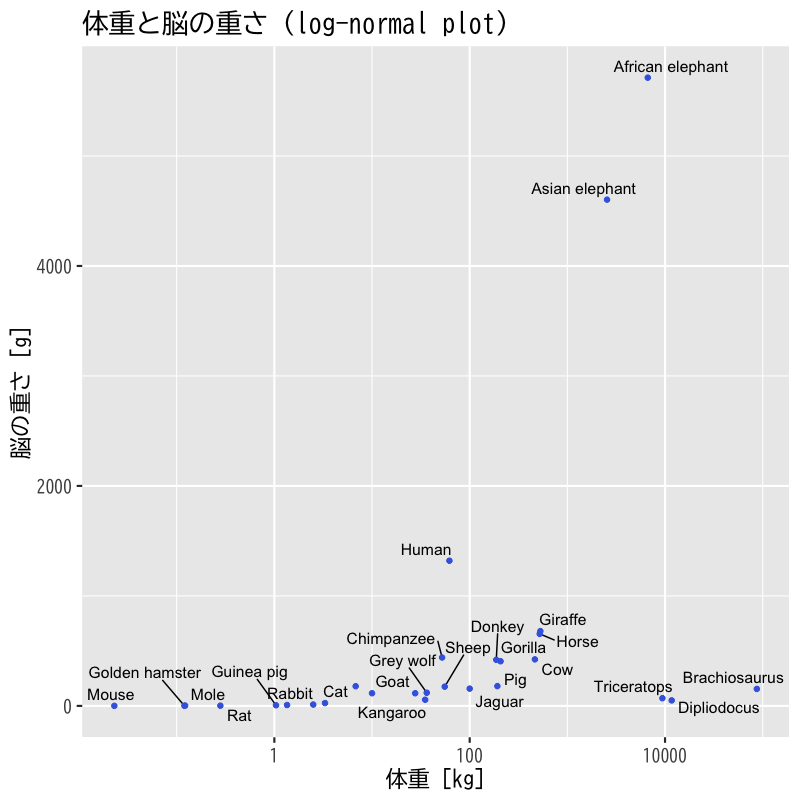
05_animals2.png

Figure 11: 体重を対数変換

  • 散布図 (xy軸を対数変換)

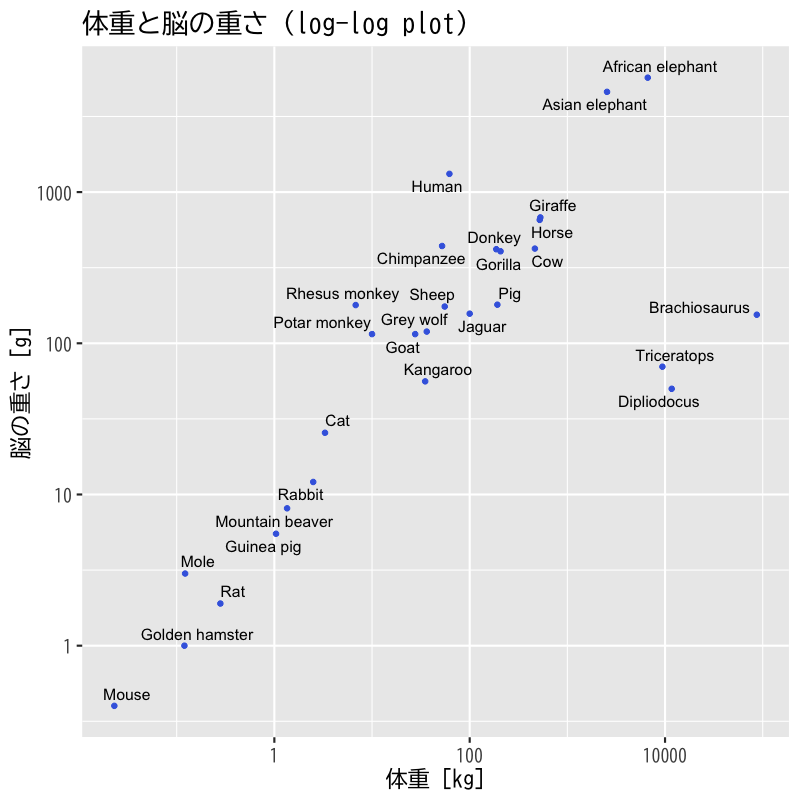
05_animals3.png

Figure 12: 体重と脳の重さを対数変換

  • 単回帰 (全データ)

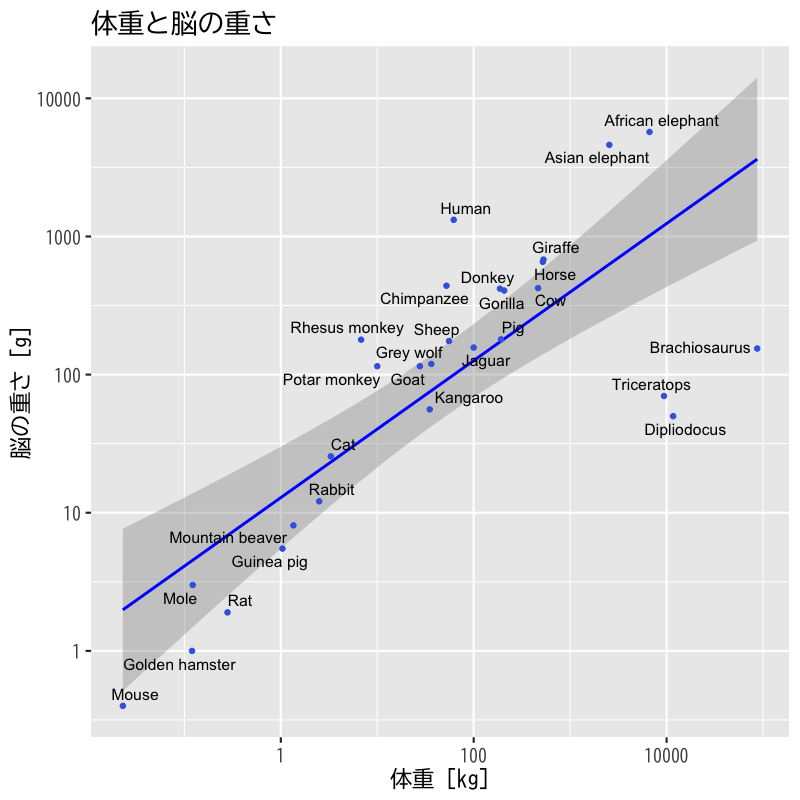
05_animals4.png

Figure 13: 回帰直線と信頼区間

  • 単回帰 (外れ値を除去)

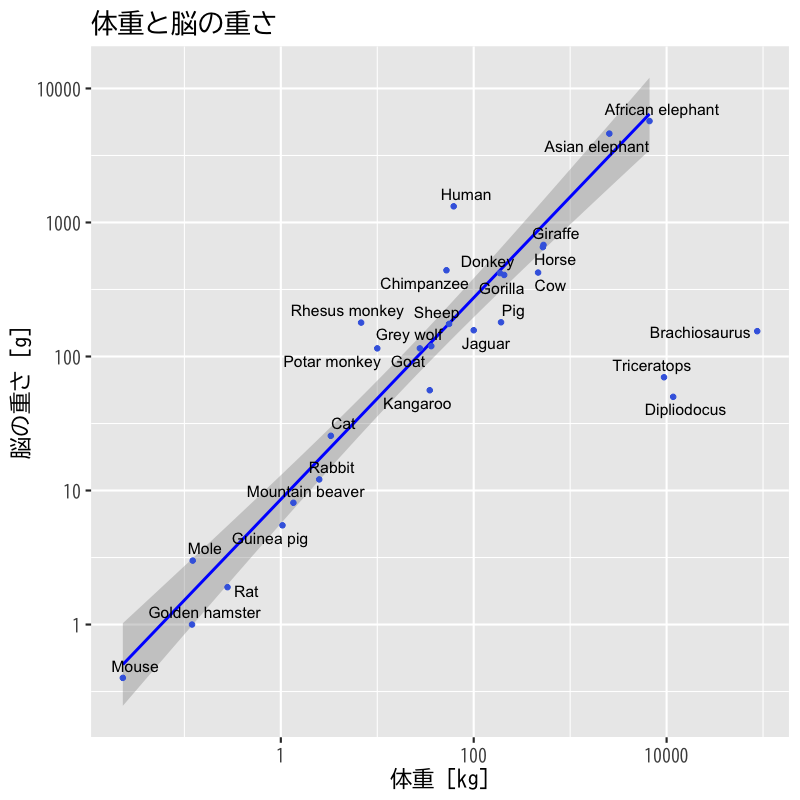
05_animals5.png

Figure 14: 外れ値を除いた回帰直線と信頼区間

非線形な関係の分析

  • 東京の気候データ(10月)を用いて 気温に影響する変数の関係を検討する
    • 日射と気圧の線形回帰モデル
      (日射と気圧が気温にどのように影響するか検討する)
    • これらの交互作用を加えた線形回帰モデル
      (日射と気圧の相互の関係の影響を検討する)

  • 関連データの散布図

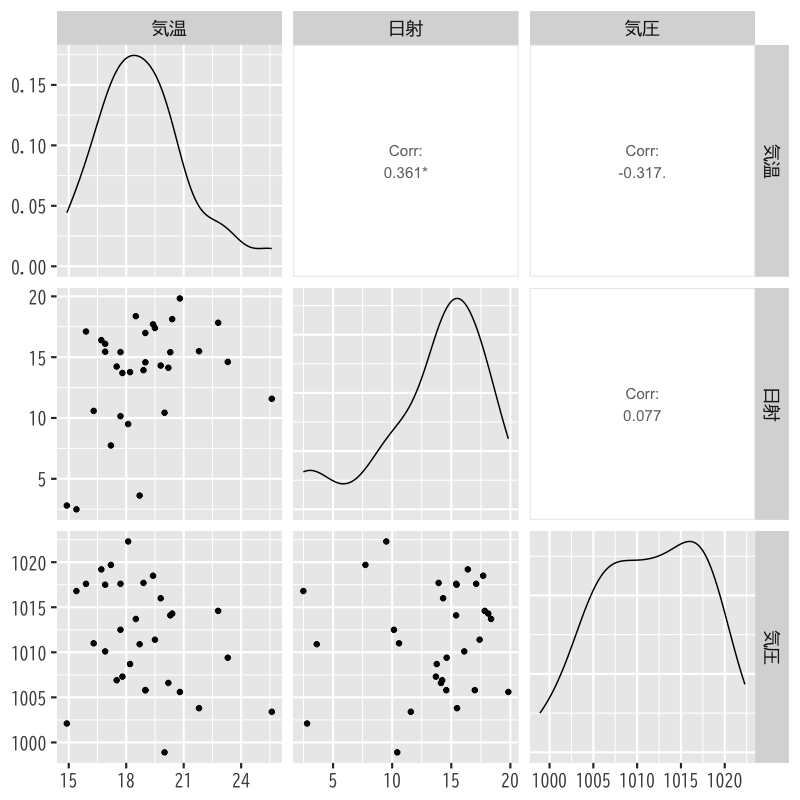
05_interaction.png

Figure 15: 気温，日射，気圧の関係

交互作用の効果

変数
交互作用なし
交互作用あり
係数(SE)1 係数(SE)1
日射 0.21(0.098)* 47(16.2)**
気圧 -0.17(0.086) 0.32(0.185)
日射 * 気圧
-0.05(0.016)**
R² 0.204 0.390
Adjusted R² 0.147 0.323
F統計量 3.58 5.77
p値 0.041 0.004
1 *p<0.05; **p<0.01; ***p<0.001
Abbreviation: SE = 標準誤差
  • 気温への寄与
    • 線形モデル
      • 日射の係数は正
      • 気圧の係数は負
    • 交互作用を加えたモデル
      • 日射の係数は気圧がある値より高い場合に負
      • 気圧の係数は日射がある値より高い場合に負
      • 係数の有意性は低いのでより多くのデータでの分析が必要

カテゴリカル変数の利用

  • 東京の気候データを用いて 気温を回帰するモデルを検討する
    • 降水の有無を表すカテゴリカル変数を用いたモデル
      (雨が降ると気温が変化することを検証する)
    • 月をカテゴリカル変数として加えたモデル
      (月毎の気温の差を考慮する)

  • 関連データの散布図

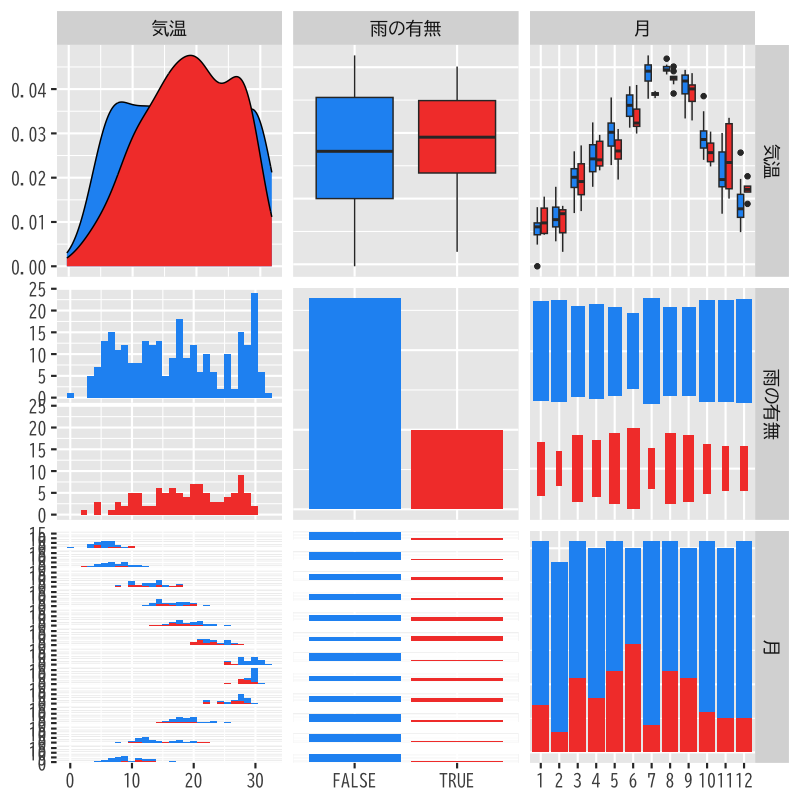
05_categorical.png

Figure 16: 気温，雨の有無，月の関係

カテゴリカル変数の効果

変数
雨の有無
雨の有無+月
係数(SE)1 係数(SE)1
雨の有無

    FALSE — —
    TRUE 1.7(0.918) -1.6(0.299)***
月

    1
—
    2
1.3(0.677)
    3
3.0(0.667)***
    4
10(0.674)***
    5
13(0.667)***
    6
16(0.672)***
    7
22(0.671)***
    8
22(0.667)***
    9
20(0.673)***
    10
14(0.670)***
    11
7.0(0.671)***
    12
0.89(0.662)
(Intercept) 17(0.537)*** 7.3(0.469)***
R² 0.009 0.906
Adjusted R² 0.006 0.903
F統計量 3.25 284
p値 0.072 <0.001
1 *p<0.05; **p<0.01; ***p<0.001
Abbreviation: SE = 標準誤差
  • 気温への寄与
    • 雨の 有無モデル
      • 経験的に雨の有無は気温と無関係ではないと考えられる
      • 決定係数から回帰式としての説明力は極めて低い
      • 通年では雨と気温の関係は積極的に支持されない
    • 雨の有無+月モデル
      • 月毎の気温の偏りが月の係数として推定される
      • 雨の日の方が気温が低いことが支持される

  • 実測値とあてはめ値の関係

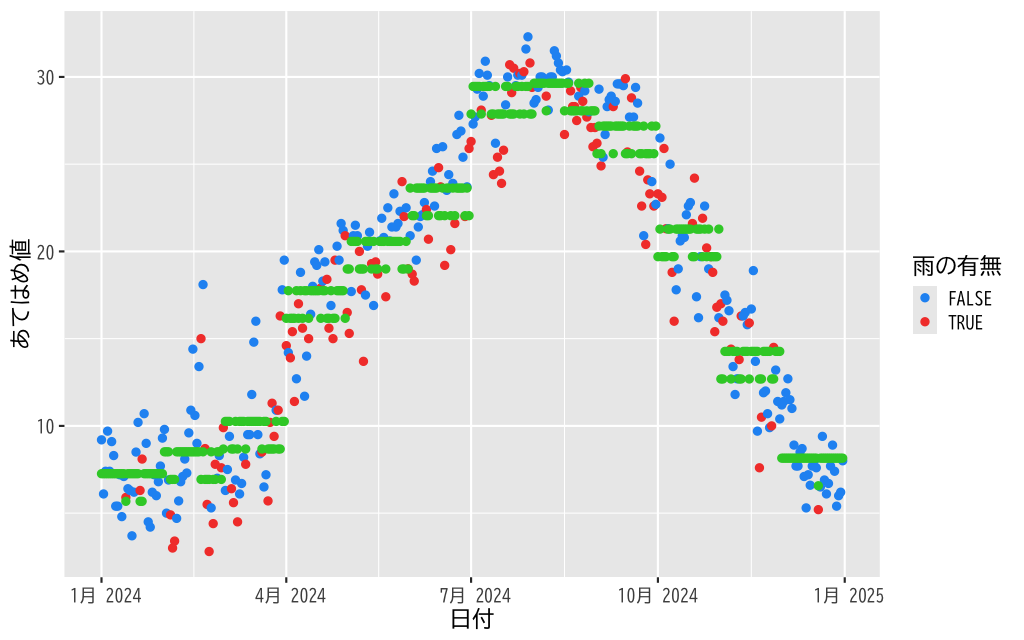
05_rain.png

Figure 17: 月毎の気温への雨の影響

次回の予定

  • 第1回: 主成分分析の考え方
  • 第2回: 分析の評価と視覚化